The document is a master's thesis by Ahmed Ben Jemia, submitted to the University of Tunis, focusing on applying machine learning techniques to revenue management for a restaurant reservation platform. It includes foundational concepts of yield and revenue management, various machine learning algorithms for forecasting, and an experimental analysis with results derived from real datasets. Key components cover yield management systems, data processes, model performance measures, and a statistical appendix.
























![Section 1.4 – Yield management forecasting methods 14
• µ is the mean of the series;
• θ(j) whit ( j = 1, 2, ..., q);
• q is the order of the model;
AR(p) and MA(q) models can be effectively combined together to form a general and
useful class of time series models, known as the ARMA(p,q) model.
Definition 1.3. (ARMA) ARMA(p,q) model is given by (Cochrane, 2005; Hipel and McLeod,
1994):
yt = c + εt +
p
i=1
φ(i)yt−i +
q
j=1
θ(j)εt−j (1.3)
where:
• p refers to autoregressive terms;
• q refers to moving average terms;
Example 1.2. Data was collected from an existing US airline. There is a sample of 5 city
pairs named A/B, B/A, D/C, E/F and F/E. A total of 28 flights (F1,F2,...,F28) were included
in the sample and final bookings for M class. Reservations data can be retrieved for the
boarding day (MBD), 7 (M7), 14 (M14), 21 (M21), 28 (M28) days before flight departure.
The sample period was from January, 1986 through June, 1986.
ARIMA(3,0,2) model were developed and estimated for flight F1 in the A/B market:
AR(3) × MBD(t) = C + MA(2) × r(t) (1.4)
where:
• AR(3) = ( 1 + AR(1) ×B + AR(2)×B2
+ AR(3) ×B3
;
• B = backward shift operator, defined as: Bn
[X(t)]= X(t-n);
• MBD(t) = final reservations, M-class at time t;
• MA(2) = ( 1 + MA(1) ×B + MA(2) × B2
);
• r(t)= residual at time t;
• C = constant;](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-25-320.jpg)









![Section 2.3 – Machine learning algorithms for regression 26
of visitors). The predicted response for an observation is given by the mean response of
the training observations that belong to the same terminal node.
Definition 2.2. The data consists of p inputs and a response, for each of N observa-
tions: that is, (xi, yi) for i = 1, 2, ..., N, with xi = (xi1, xi2, ..., xip). The algorithm needs
to automatically decide on the splitting variables and split points, and also what topol-
ogy (shape) the tree should have. Suppose first that there is a partition into M regions
R1, R2, ..., RM, and the response model will be like a constant cm in each region:
f(x) =
M
m=1
cmI(x ∈ Rm) (2.5)
If the minimization criterion will be adopted of the sum of squares (yi − f(xi))2
, it’s easy
to see that the best ˆcm is just the average of yi in region Rm:
ˆcm = avg(yi | xi ∈ Rm) (2.6)
Finding the best binary partition in terms of minimum sum of squares is usually not com-
putationally feasible, so the greedy algorithm will proceed. Starting with all data, a divi-
sion variable j and a division point s will be considered, and the pair of half-planes will
be defined.
R1(j, s) = {X | Xj s} and R2(j, s) = {X | Xj > s} (2.7)
Next, look for the splitting variable j and split point s that solve:
min
j,s
[ min
c1
xi∈R1(j,s)
(yi − c1)2
+ min
c2
xi∈R2(j,s)
(yi − c2)2
] (2.8)
For any choice j and s, the inner minimization is solved by
ˆc1 = avg (yi | xi ∈ R1(j, s)) and ˆc2 = avg (yi | xi ∈ R2(j, s)) (2.9)
For each splitting variable, the determination of the split point s can be performed very
quickly and, therefore, by scanning all inputs, the determination of the best pair (j, s) is
possible. Once the best split has been found, the data must be divided into two resulting
regions and the process of dividing on each of the two regions must be repeated. Then
this process is repeated on all resulting regions.
Tree size is a tuning parameter governing the model’s complexity, and the optimal
tree size should be adaptively chosen from the data. One approach would be to split tree
nodes only if the decrease in sum-of-squares due to the split exceeds some threshold. This](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-37-320.jpg)
![Section 2.3 – Machine learning algorithms for regression 27
strategy is too short-sighted, however, since a seemingly worthless split might lead to a
very good split below it.
The preferred strategy is to grow a large tree T0, stopping the splitting process only
when some minimum node size (say 5) is reached. Then this large tree is pruned using
cost-complexity pruning.
Suppose a sub-tree T ⊂ T0 to be any tree that can be obtained by pruning T0, that
is, collapsing any number of its internal (non-terminal) nodes. The terminal nodes are
indexed by m, with node m representing region Rm. Let |T| denote the number of terminal
nodes in T.
Nm = # {xi ∈ Rm};
ˆcm =
1
Nm xi∈Rm
yi;
Qm(T) =
1
Nm xi∈Rm
(yi − ˆcm)2
;
(2.10)
The cost complexity criterion is:
Cα(T) =
|T|
m=1
NmQm(T) + α|T| (2.11)
The idea is to find, for each α, the sub-tree Tα ⊆ T0 to minimize Cα(T). The tuning
parameter α 0 governs the trade-off between tree size and its goodness of fit to the data.
Large values of α result in smaller trees Tα, and conversely for smaller values of α. As the
notation suggests, with α = 0 the solution is the full tree T0. How to adaptively choose
α? For each α one can show that there is a unique smallest sub-tree Tα that minimizes
Cα(T). To find Tα, use weak link pruning: successively collapse the internal node that
produces the smallest increase per node of m NmQm(T), and continue until producing
the single node (root) tree. This gives a (finite) sequence of sub-trees, and one can show
this sequence must contain Tα.
Example 2.2. , Figure 2.5 explains the popular method for tree-based regression called
CART with our data base. we took as independent variables X all the attributes of the
database except the number of visitors. For the dependent variable y we took the number
of visitors. A detailed description of the database will be presented in Subsection 3.2.1.
We can say that:
If X[6] ≤ 0.645 and X[6] ≤ 1.562 and X[6] ≤ 2.545 then predict 1.628.
If X[6] ≤ 0.645 and X[6] ≤ 1.562 and X[6] ≤ 1.16 then predict 0.646.
If X[6] ≤ 0.645 and X[6] ≤ −0.438 and X[6] ≤ −1.752 then predict -0.588.
If X[6] ≤ 0.645 and X[6] ≤ −0.438 and X[6] ≤ 0.212 then predict 0.01.](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-38-320.jpg)

![Section 2.3 – Machine learning algorithms for regression 29
preferred choice. RF can be used for either classification and regression.
Example 2.3. For random forests, we will work on the same example of the data set
explained in Subsection 2.3.2. We train a random forest with 10 estimators, and maximal
depth = 3 on our data set. The random forest model is then an ensemble model of 10
regression tree estimators, each of them has a maximal depth equal to 3 (See Figure 2.6).
Note that variable X[6] corresponding to annual average visitors is present on several
nodes in all the trees of the trained random forest. It suggest that this feature is the most
informative. This observation is also confirmed by Figure 3.21 (See Subsection 3.2.7 for
more details about feature importance).](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-40-320.jpg)





![Section 2.3 – Machine learning algorithms for regression 35
following pseudo-code.
Algorithm 4: K-Nearest Neighbors regression (KNNR) algorithm
Input: A n × n distance matrix D[1...n, 1...n] and an index s of the starting city.
Result: A list Path of the vertices containing the tour is obtained
1 for i ← 1 to n do
2 Visited [i] ← false;
3 end
4 Initialize the list Path with s;
5 Visited[s] ← true;
6 Current ← s;
7 for i ← 2 to n do
8 Find the lowest element in row current and unmarked column j containing
the element;
9 Current ← j;
10 Visited[j] ← true;
11 Add j to the end of list Path;
12 end
13 Add s to the end of list Path;
14 return Path
2.3.6 Stochastic gradient descent (SGD)
Definition 2.5. (Stochastic gradient descent) Let us first consider a simple supervised
learning setup. Each example z is a pair (x, y) composed of an arbitrary input x and a
scalar output y. We consider a loss function (ˆy, y) that measures the cost of predicting ˆy
when the actual answer is y, and we choose a family F of functions fw(x) parameterized by
a weight vector w. We seek the function f ∈ F that minimizes the loss Q(z, w) = (fw(x), y)
averaged on the examples. Although we would like to average over the unknown distri-
bution dP(z) that embodies the Laws of Nature, we must often settle for computing the
average on a sample z1...zn.
E(f) = (f(x), y) dP(z)
En(f) =
1
n
n
i=1
( f(xi), yi)
(2.19)
where:
• The empirical risk En(f) measures the training set performance.](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-46-320.jpg)

















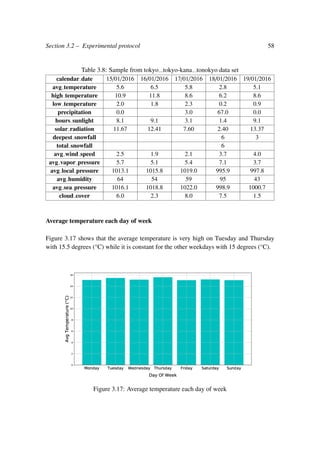







![Section 3.2 – Experimental protocol 66
tion, we decided to fit an ARIMA model of statsmodels, which is a Python module that
provides classes and functions for the estimation of many different statistical models, as
well as for conducting statistical tests, and statistical data exploration. The results are
mentioned in Table 3.15.
Table 3.14: ARMA model results
ARMA Model Results
Dep. Variable: y No. Observations: 93
Model: ARMA(0, 1) Log Likelihood -423.244
Method: css-mle S.D. of innovations 22.904
Date: Friday, 05 June 2020 AIC 852.488
Time: 13:13:08 BIC 860.085
Sample: 0 HQIC 855.555
coef std err z P > |z| [0.025 0.975]
const 45.1657 3.234 13.966 0.000 38.827 51.504
ma.L1.y 0.3655 0.091 4.026 0.000 0.188 0.543
Roots
Real Imaginary Modulus Frequency
MA.1 -2.7360 +0.0000j 2.7360 0.5000
Seasonal AutoRegressive Integrated Moving Average with eXogenous regressors (SARI-
MAX) model
SARIMAX is ARIMA, but with capability for modeling seasonality and support for ex-
ogenous variables (For more details, see Appendix A). Figure 3.24 shows that the residues
are approximately normally distributed. There does not appear to be a model for the resid-
uals, but there are some outliers. Overall, we find that this model has been successful in
capturing the patterns in the data.](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-77-320.jpg)
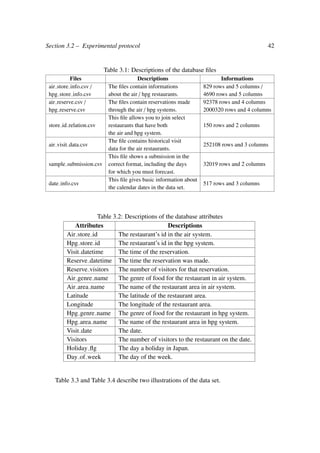
![Section 3.2 – Experimental protocol 67
Figure 3.24: ACF, PACF and residuals plots for SARIMAX
The results are mentioned in Table 3.15.
Table 3.15: Sarimax model results
Statespace Model Results
Dep. Variable: y No. Observations: 93
Model: SARIMAX(2, 0, 0, 7) Log Likelihood -328.688
Date: Friday, 05 June 2020 AIC 665.375
Time: 20:15:00 BIC 674.853
Sample: 0 HQIC 669.172
-93
Covariance Type: opg
coef std err z P > |z| [0.025 0.975]
intercept 5.9385 4.353 1.364 0.173 -2.594 14.471
ar.S.L7 0.5044 0.104 4.871 0.000 0.301 0.707
ar.S.L14 0.3530 0.125 2.827 0.005 0.108 0.598
sigma2 240.6486 28.682 8.390 0.000 184.433 296.864
Ljung-Box (Q): 15.53 Jarque-Bera (JB): 9.36
Prob(Q): 1.00 Prob(JB): 0.01
Heteroskedasticity (H): 1.13 Skew: -0.20
Prob(H) (two-sided): 0.75 Kurtosis: 4.64](https://image.slidesharecdn.com/masterahmedbenjemia-201208103331/85/Applying-Machine-Learning-Techniques-to-Revenue-Management-78-320.jpg)