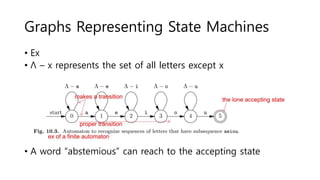
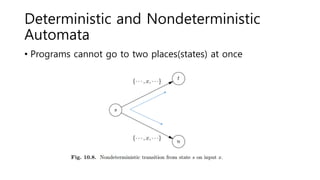
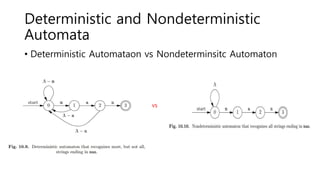
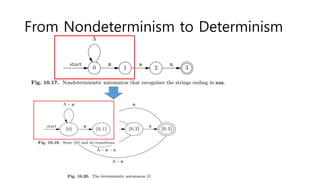
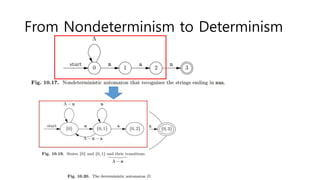
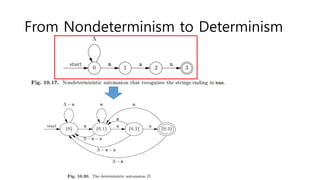
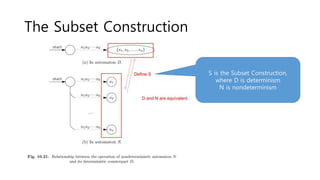
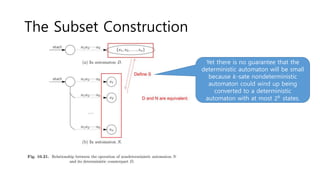
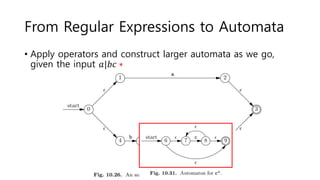
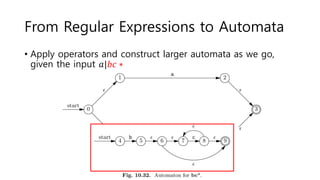
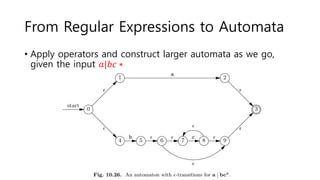
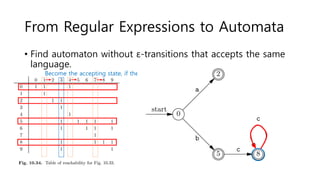
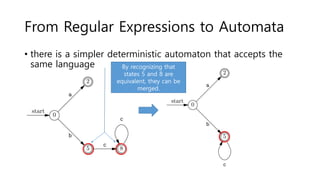
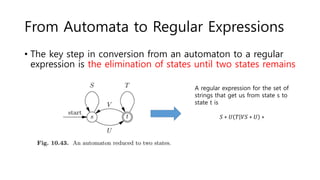
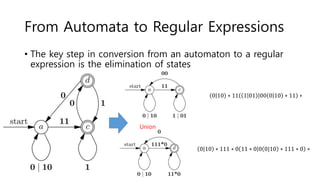
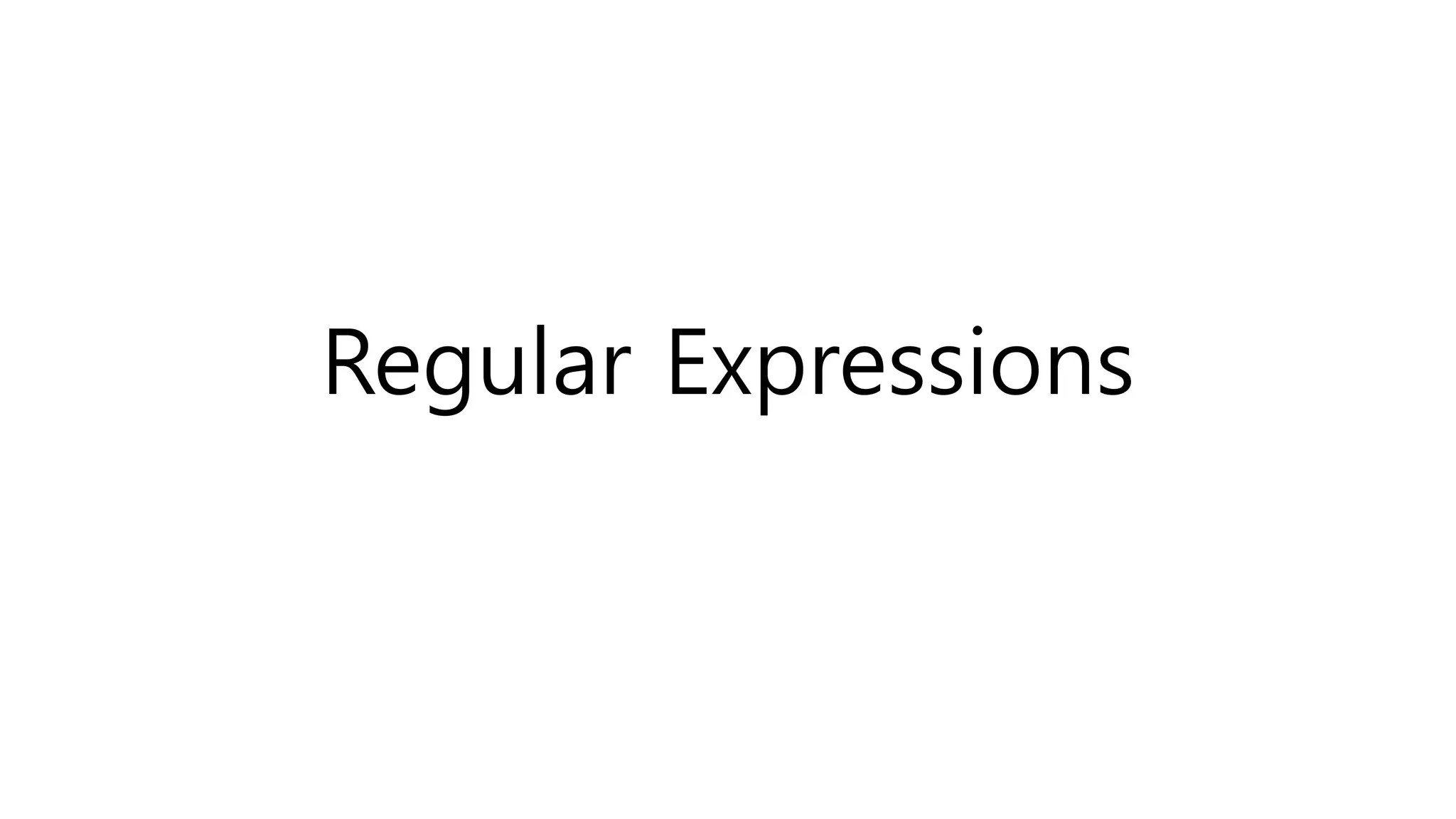The document discusses regular expressions and finite automata. It explains that an automaton is a finite representation of a formal language and can be represented as a state machine graph. Regular expressions define patterns using operators and can be converted to equivalent nondeterministic and deterministic finite automata. The subset construction algorithm can determinize a nondeterministic automaton. Converting between regular expressions and automata allows problems to be solved using different representations.