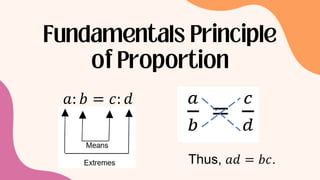
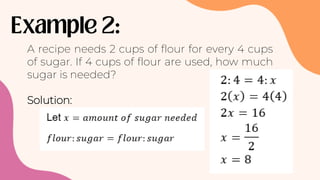Ratios compare quantities of the same type and can be written using a colon, fraction, or "to". Proportions state that two ratios are equal, such as a:b = c:d. To solve proportions, the product of the extremes equals the product of the means. For example, if a recipe calls for 2 cups of flour for every 4 cups of sugar, and 4 cups of flour are used, the proportion 2:4 = x:4 can be set up and solved to find the amount of sugar needed is 6 cups.

2. is a comparison of two numbers with the
same units, or different units of the same
kind. It is obtained by dividing the first
number by the second number.

3. The ratio of to can be written as:
1.Using a colon – 𝑎: 𝑏
2.Using a fraction –
𝑎
𝑏
3.Using the word “to” – 𝑎 𝑖𝑠 𝑡𝑜 𝑏

4. If there are 13 female teachers and three (3)
male teachers in DNAMNHS, then the ratio
of female to male teacher is 13:3.

5. Matias has a bag with 4 ball pens, 2
rosaries, and 5 books.
• What is the ratio of ball pens to
rosaries?
• What is the ratio of books to ball pens?
• What is the ratio of rosaries to the total
number of items in the bag?

6. is a statement indicating the
equality of two ratios.

7. If a:b and c:d are two equivalent ratios, then 𝑎: 𝑏 =
𝑐: 𝑑 is a proportion.
The proportion 𝑎: 𝑏 = 𝑐: 𝑑 may also be written
as. This may be read as
𝑎
𝑏
=
𝑐
𝑑
. This may be read as
"𝑎 𝑖𝑠 𝑡𝑜 𝑏 𝑎𝑠 𝑐 𝑖𝑠 𝑡𝑜 𝑑. "
• Term – each of a,b,c, and d
• Extremes – the two outer terms (a and d)
• Means – the two inner terms (b and c)

8. 𝑎: 𝑏 = 𝑐: 𝑑
Thus, 𝑎𝑑 = 𝑏𝑐.

9. Find the mean proportional between 3 and 12.
Solution:
The mean proportional
between 3 and 12 is 6 or -6.

10. A recipe needs 2 cups of flour for every 4 cups
of sugar. If 4 cups of flour are used, how much
sugar is needed?
Solution: