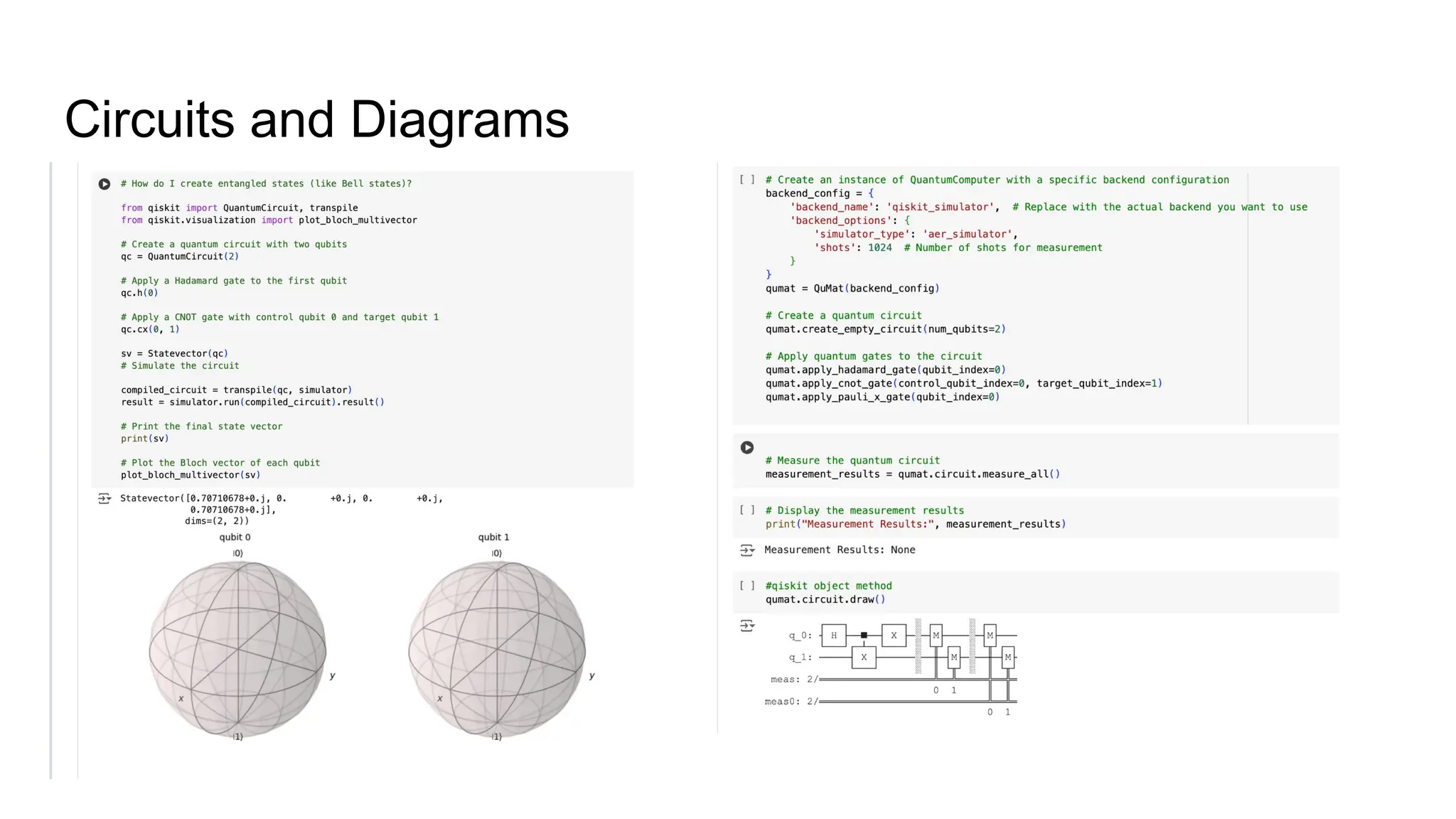
The document provides an introduction to Apache Mahout's newly integrated quantum computing interface, QUMAT, highlighting its capabilities in distributed matrix arithmetic and integration with various quantum programming frameworks. It outlines Mahout's history, motivations for utilizing quantum computing, and examples of its syntax for advanced mathematical operations. The document also encourages community involvement through contributions and testing opportunities.

1. QuMat
Apache Mahout's Quantum Computing Interface
Andrew Musselman
FOSSY
Portland OR
Aug 2024

2. ● Intro to Mahout
● Intro to Quantum
● Motivation for Quantum in Mahout
● Distributed Matrix Arithmetic
● Rationale for QuMat
● Logic Gates in QuMat
● Notebook Demo
● Circuits and Diagrams
● Next Steps
● How to Get Involved
Agenda

3. Apache Mahout is a distributed linear algebra framework and mathematically
expressive Scala DSL designed to let mathematicians, statisticians, and data
scientists quickly implement their own algorithms.
● Mathematically Expressive Scala DSL
● Support for Multiple Distributed Backends (including Apache Spark)
● Modular Native Solvers for CPU/GPU/CUDA Acceleration
Intro to Mahout

4. ● 2008: Lucene sub-project with analytics including clustering
● 2010: Apache top-level project recommender system
● Taste: (https://svn.apache.org/repos/asf/lucene/mahout/site/publish/taste.pdf?p=836600)
● 2015: Samsara (back-end independent programming environment)
● 2017: Hadoop MapReduce back-end deprecated
● 2020: 14.1 released
● 2022: Zeppelin integration and algorithm development framework
● 2024: QuMat quantum computing interface
Intro to Mahout

5. Intro to Quantum

6. Intro to Quantum
Classical bit
21
states, ("0" or "1")
Quantum bit ("qubit")
2n
states, ("it's complicated")

7. Intro to Quantum
* https://en.wikipedia.org/wiki/Quantum_logic_gate
Quantum states are typically represented by "kets," from a notation
known as bra–ket. The vector representation of a single qubit is
|a⟩ = v0 |0⟩ + v1 |1 →
⟩
where v0 and v1 are the complex probability amplitudes of the qubit,
and the values zero and one are represented by the kets
|0⟩ = and |1⟩ =
v0
v1

8. |0⟩ = and |1⟩ =
These kets are basis vectors for a complex vector space. Logic gates in
quantum computing are matrices which take actions on qubits.
For example, the identity gate (identity matrix) performs no action on any qubit:
= =
Intro to Quantum
v0 * 1 + v1 * 0
v0
v1 v0 * 0 + v1 * 1
v0
v1

9. Motivation for Quantum in Mahout
● Core capabilities of Mahout
○ Matrix arithmetic and operations
○ Linear algebra
○ Back-end agnostic, distributed or in-core CPU or GPU
○ Simplified syntax in matrix math DSL (Samsara)
○ Management of large-scale vectors and matrices
● Quantum compute in essence is matrix arithmetic
○ Circuits are composed by multiplying matrices
○ Vectors and matrices are complex-valued instead of binary or real

10. Samsara DSL and Syntax
Samsara A’A
val C = A.t %*% A
MLLib A’A
val C = A.transpose().multiply(A)

11. Samsara DSL and Syntax
Computation in distributed stochastic PCA (dSPCA):
In Samsara DSL:
val G = B %*% B.t - C - C.t + (xi.t dot xi) * (s_q.t cross
s_q)

12. // Dense matrices:
val A = dense((1, 2, 3), (3, 4, 5))
// Sparse matrices:
val A = sparse(
(1, 3) :: Nil,
(0, 2) :: (1, 2.5) :: Nil
)
Instantiating Matrices

13. Arithmetic and Assignment
// Plus/minus:
a + b
a - b
a + 5.0
a - 5.0
// Hadamard (elementwise) product:
a * b
a * 0.5
// Operations with
assignment:
a += b
a -= b
a += 5.0
a -= 5.0
a *= b
a *= 5

14. Other Operators
// Optimized right and left multiply
with a diagonal matrix:
diag(5, 5) :%*% b
A %*%: diag(5, 5)
// Second norm, of a vector or matrix:
a.norm
// Transpose:
val Mt = M.t
// Dot product:
a dot b
// Cross product:
a cross b
// Matrix multiply:
a %*% b

15. Distributed Matrix Arithmetic: Optimization of A'A
A

16. Distributed Matrix Arithmetic: Optimization of A'A
x
A
AT

17. Distributed Matrix Arithmetic: Optimization of A'A
x = x
A
AT
a1
T
a1

18. Distributed Matrix Arithmetic: Optimization of A'A
x = x + x
A
AT
a1
T
a1 a2
T
a2

19. Distributed Matrix Arithmetic: Optimization of A'A
x = x + x
A
AT
a1
T
a1 a2
T
a2
+ x
a3
T
a3

20. Distributed Matrix Arithmetic: Optimization of A'A
x = x + x
A
AT
a1
T
a1 a2
T
a2
+ x
a3
T
a3
+ x
a4
T
a4

21. Rationale for QuMat
● Multiple frameworks for programming quantum circuits
○ Qiskit (IBM)
○ Braket (AWS)
○ Cirq (Google)
○ TKET (Honeywell)
○ Qsharp (Microsoft)
○ Pyquil (Rigetti)
● Multiple vendor platforms for running on simulated or real quantum hardware
○ IBM (https://quantum.ibm.com)
○ AWS (https://aws.amazon.com/braket)
○ Google (https://quantumai.google/quantumcomputer)
○ Honeywell (https://www.honeywell.com/us/en/company/quantum/quantum-computer)
● Multiple frameworks and back-ends is a Mahout core value
● One interface with no code change across tools provides flexibility

22. ● Logic gates implemented
○ Qiskit
○ Cirq
○ Braket
● Next steps
○ Draw
○ Measure
○ Execute
QuMat Current State
Samsara QuMat
Spark Flink … Qiskit Cirq Braket
Mahout

23. Logic Gates in QuMat
Function definitions in Python

24. Notebook Demo

25. Circuits and Diagrams

26. Next Steps
● Draw, measure, and execute methods
● Use cases
● More examples
● Quantum machine learning methods (QML)

27. How to Get Involved
● Try it out using Docker
● Subscribe to the user@mahout.apache.org and dev@mahout.apache.org
mailing lists
● Get a binary or source build
● Run a notebook straight out of GitHub
● Contribute some documentation, fix some bugs, add some features

28. Q&A
Thank You!