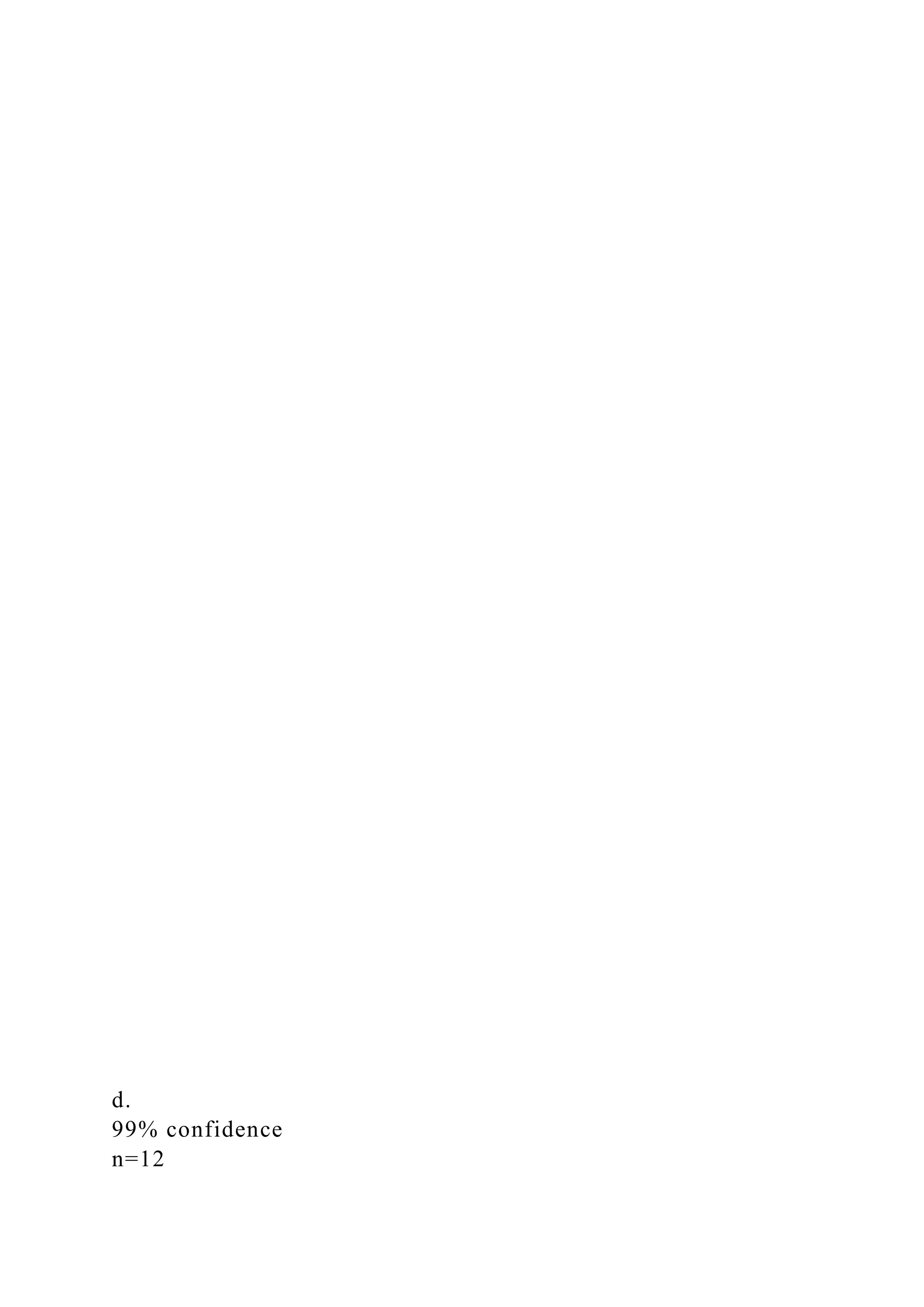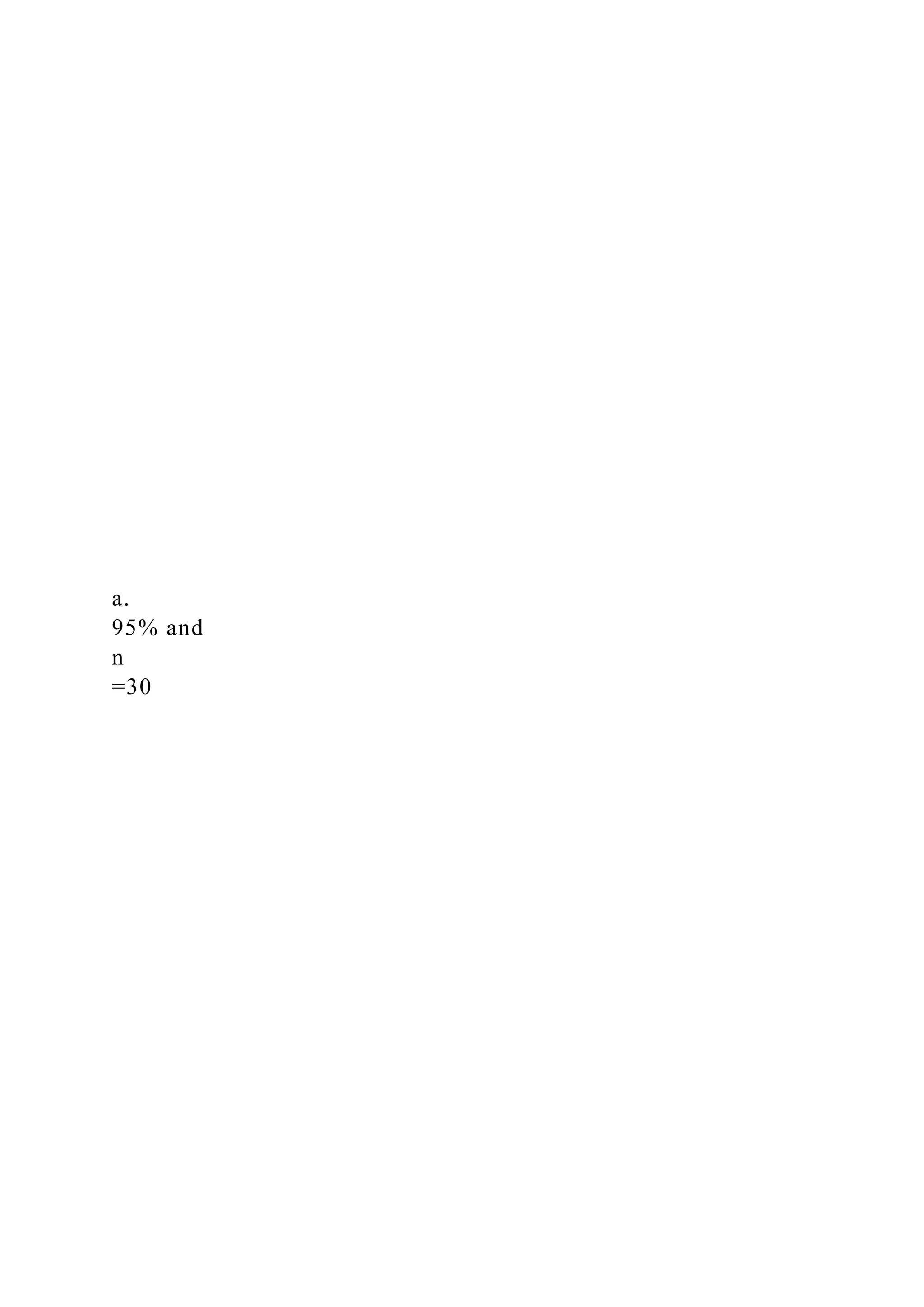The document details statistical concepts related to the construction of confidence intervals, hypothesis testing, and data analysis using various distributions (t, z, and chi-squared). It covers practical examples, including estimating GPA confidence intervals for students, testing participation rates in health screenings, and comparing achievement test scores over time. Additionally, it includes problems and multiple-choice questions on linear relationships and data interpretations.

1. Problems related to text's Chapter 7:

2. 1.
Assume you need to build a confidence interval for a population
mean within some given situation. Naturally, you must
determine whether you should use either the t-distribution or the
z-distribution or possibly even neither based upon the
information known/collected in the situation. Thus, based upon
the information provided for each situation below, determine
which (
t
-,
z
- or neither) distribution is appropriate. Then
if
you can use either a t- or z- distribution, give the associated
critical value (critical
t
- or
z
- score) from that distribution to reach the given confidence
level.

5. a.
99% confidence
n=150
σ known
population data believed to be very skewed

6. Appropriate distribution:

7. Associated critical value:

8. b.
95% confidence
n=10
σ unknown
population data believed to be normally distributed

9. Appropriate distribution:
Associated critical value:

11. c.
90% confidence
n=40
σ
unknown
population data believed to be normally distributed
Appropriate distribution:

12. Associated critical value:

13. d.
99% confidence
n=12

14. σ unknown
population data believed to be very skewed
Appropriate distribution:

15. Associated critical value:

18. 2.
A student researcher is interested in determining the average (
µ
) GPA of all FHSU students, in order to investigate grade
inflation at regional universities. The data below represent the
GPA's of thirty randomly selected FHSU students.

19. 2.75
2.55
3.95
1.74
2.66
3.10
2.41
1.57
2.12
3.67
3.56
1.98
4.00
3.21
1.95
3.75

20. 1.45
3.01
2.29
2.66
3.95
2.50
3.88
2.79
2.32
3.44
2.07
0.62
2.72
3.55
3.92
3.41
2.14
1.15
2.75
3.25

21. a.
How do you know that you will need to construct the confidence
interval using a
t
-distribution approach as opposed to a
z
-distribution?

24. We want to construct the mean value confidence interval for the
GPA's with a 90% confidence level.
b.
Determine the best point estimate (average) for the mean GPA.

26. c.
Determine the critical
t
-value(s) associated with the 95% confidence level.

28. d.
Determine the margin of error.

30. e.
Determine the confidence interval.

32. f.
In a sentence, interpret the contextual meaning of your result to
part e above...that is relate the values to this situation regarding
the mean GPA's of all FHSU students.

36. 3.
Determine the two chi-squared (
χ
2
) critical values for the following confidence levels and sample
sizes.

37. a.
95% and
n
=30

39. b.
99% and
n
=20

43. 4.
We are also interested in estimating the population standard
deviation (σ) for all FHSU student GPA's. We will assume that
GPA's are at least approximately normally distributed. Below
are the GPA's.

44. 2.75
2.55
3.95
1.74
2.66
3.10

45. 2.41
1.57
2.12
3.67
3.56
1.98
4.00
3.21
1.95
3.75
1.45
3.01
2.29
2.66
3.95
2.50
3.88
2.79

46. 2.32
3.44
2.07
0.62
2.72
3.55
3.92
3.41
2.14
1.15
2.75
3.25

47. Out to the right, construct a 95% confidence interval estimate of
sigma (σ), the population standard deviation.

51. Problems related to text's Chapter 8:

52. 5.
(Multiple Choice) A hypothesis test is used to test a claim. On
a right-tailed hypothesis test with a 1.39 critical value, the
collected sample's test statistic is calculated to be 1.45. Which
of the following is the correct decision statement for the test?

53. A.
Fail to reject the null hypothesis
B.
Reject the null hypothesis

54. C.
Claim the alternative hypothesis is true
D.
Claim the null hypothesis is false

56. 6.
(Multiple Choice) A hypothesis test is used to test a claim. A
P
-value of 0.08 is calculated on the hypothesis test with a
significance level set at 0.05. Which of the following is the
correct decision statement for the test?

57. A.
Claim the null hypothesis is true

58. B.
Claim the alternative hypothesis is false
C.
Reject the null hypothesis

59. D.
Fail to reject the null hypothesis

61. 7.
(Multiple Choice) Which of the following is
not
a requirement for using the
t
-distribution for a hypothesis test concerning
μ
.
A.
Sample size must be larger than 30

62. B.
Sample is a simple random sample
C.
The population standard deviation is unknown

64. 8.
In an effort to promote healthy lifestyles, health screenings are
given to employees of a large corporation. In running a
promotional trial, 84 out of the 150 people who work in
one

65. office for the corporation participate in the health screening.

66. a.
Is the above information sufficient for you to be completely
certain that
more than
50% of
all
employees of the corporation will participate in the health
screening? Why or why not?

69. b.
In establishing a statistical hypothesis testing of this situation,
give the required null and alternative hypotheses for such a test,
if it is desired that more than 50% of the employees participate
in the health screening.

70. H
0
:

71. H
1
:

73. c.
Based on your answer in part b, should you use a right-tailed, a
left-tailed, or a two-tailed test? Briefly explain how one
determines which of the three possibilities is to be used.

78. d.
Describe the possible Type I error for this situation--make sure
to state the error in terms of the percent of employees in the
corporation who will participate in the health screenings.

81. e.
Describe the possible Type II error for this situation--make sure
to state the error in terms of the percent of employees in the
corporation who will participate in the health screenings.

85. f.
Determine the appropriate critical value(s) for this situation
given a 0.025 significance level.

88. g.
Determine/calculate the value of the sample's test statistic.

90. h.
Detemine the
P
-value.

93. i.
Based upon your work above, is there statistically sufficient
evidence in this sample to support that more than 50% of
employees will participate in the health screening? Briefly
explain your reasoning.

98. 9.
The mean score on a certain achievement test at the turn of the
century was 74. However, national standards have been
implmented which may lead to a change in the mean score. A
random sample of 40 scores on this exam taken this year yeilded
the following data set. At a 10% significance level, test the
claim that the mean of all current test scores is not the same as
in 2000.

99. 85
77
74
88
89
66
0
70

100. 73
76
86
74
73
82
72
0

101. 82
82
80
76
87
76
77
67
72
49
73
75

102. 82
73
81
30
58
75
72
89
76
18
72
74

104. a.
Give the null and alternative hypotheses for this test in
symbolic form.
H
0
:

105. H
1
:

106. b.
Determine the value of the test statistic.

109. c.
Determine the appropriate critical value(s).

111. d
Detemine the
P
-value.

113. e.
Is there sufficient evidence to support the claim that the mean
achivement score is now different than 73? Explain your
reasoning.

117. Problem related to text's Chapter 9:
10.
Listed below are pretest and posttest scores from a study.
Using a 5% significance level, is there statistically sufficient
evidence to support the claim that the posttest scores were the
higher than the pretest scores? Perform an appropriate

118. hypothesis test showing necessary statistical evidence to
support your final given conclusion.

120. PreTest
PostTest
24
25

121. 11
12

122. 14
16
25
24

123. 17
16

124. 28
29

125. 22
23

129. Problems related to text's Chapter 10:
11.
Multiple Choice:
For each of the following data sets, choose the most appropriate
response from the choices below the table.

130. Data Set #1
Data Set #2

131. x
y
x
y
0
19
10
100

132. 1
15
14
33

133. 2
13
18
124
3
12

134. 24
160
4
7
27
65

135. 5
0
32
117

136. 6
-3
36
27
7
-4
40
150

137. 8
-7
45
44

138. A.
A strong positive linear relation exists
A.
A strong positive linear relation exists
B.
A strong negative linear relation exists
B.
A strong negative linear relation exists

139. C.
A curvilinear relation exists
C.
A curvilinear relation exists

140. D.
No linear relation exists
D.
No linear relation exists

142. 12.
Create a paired data set with 5 data points indicating strong (but
not perfect) positive linear correlation. Determine the

143. correlation coefficient value for your data

144. x
y

150. 13.
To answer the following, use the given data that contains
information on the age of eight randomly female staff members
at FHSU and their corresponding pulse rate.

151. Age (years)
Pulse Rate (bpm)

152. 42
98
34

153. 80
49
98

154. 27
63

155. 42
84
18
49

156. 41
80

157. 21
55

159. a.
Construct a scatterplot for this data set in the region to the right
(age as the independent variable, and pulse rate as the
dependent.)

161. b.
Based on the scatterplot, does it look like a linear regression
model is appropriate for this data? Why or why not?

165. c.
Add the line-of-best fit (trend line/linear regression line) to
your scatterplot. Give the equation of the trend line below.
Then give the slope value of the line and explain its meaning to
this context.

168. d.
Determine the value of the correlation coefficient. Explain
what the value tells you about the data pairs?

172. e.
Does the value of the correlation coefficient tell you there is or
is not statistically significant evidence that correlation exists
between the age and pulse rates of female staff members?
Explain your position. (HINT: application of table A-6 is
needed!)

176. f.
Based on the above, what is the best predicted pulse rate of a 30
year old female staff member?