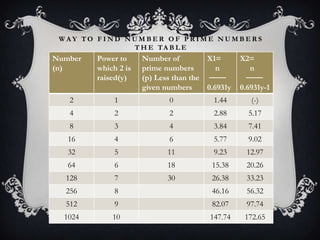
This document discusses methods for finding the number of prime numbers before a given number n raised to consecutive powers y. It presents two variables, X1 and X2, that can determine the range of prime numbers before n^y. X1 and X2 are formulas involving n, y, and the natural logarithm. It also includes a table showing the number of prime numbers less than example values of n raised to consecutive powers of y, and the corresponding values of X1 and X2.

1. PRIME NUMBERS
N O. 1 T O P I C T O B E S T U D I E D
T H O U G H 1 I T S E L F I S N O T A P R I M E 

2. WAY S TO FIND NUMBE R OF PRIME
NUMBE RS
 The notion of how many prime numbers come before a particular number
‘n’ which is raised to consecutive powers ‘y’, starting from 1, is given by the
two variables x1 and x2.
 Where x1 and x2 determine the range of the required prime numbers
before n^y.
 The results tend to the numbers which we would get on counting.
However, after a certain numbers, this method of counting becomes
impossible to use, indicating the indispensability of the aforementioned
variables.

3. X1 = n / ln(n)y
X2 = n / ln(n)y - 1
where n = the given number
y = the power to which n is raised
ln = Natural Logarithm

4. I GIVE YOU 50 MILLI SECS!!

5. W A Y T O F I N D N U M B E R O F P R I M E N U M B E R S
T H E TA B L E
Number
(n)
Power to
which 2 is
raised(y)
Number of
prime numbers
(p) Less than the
given numbers
X1=
n
───
0.6931y
X2=
n
───
0.6931y-1
2 1 0 1.44 (-)
4 2 2 2.88 5.17
8 3 4 3.84 7.41
16 4 6 5.77 9.02
32 5 11 9.23 12.97
64 6 18 15.38 20.26
128 7 30 26.38 33.23
256 8 46.16 56.32
512 9 82.07 97.74
1024 10 147.74 172.65

6. A
PRESENTATION BY
SRISHTI
SEC N
Thank You