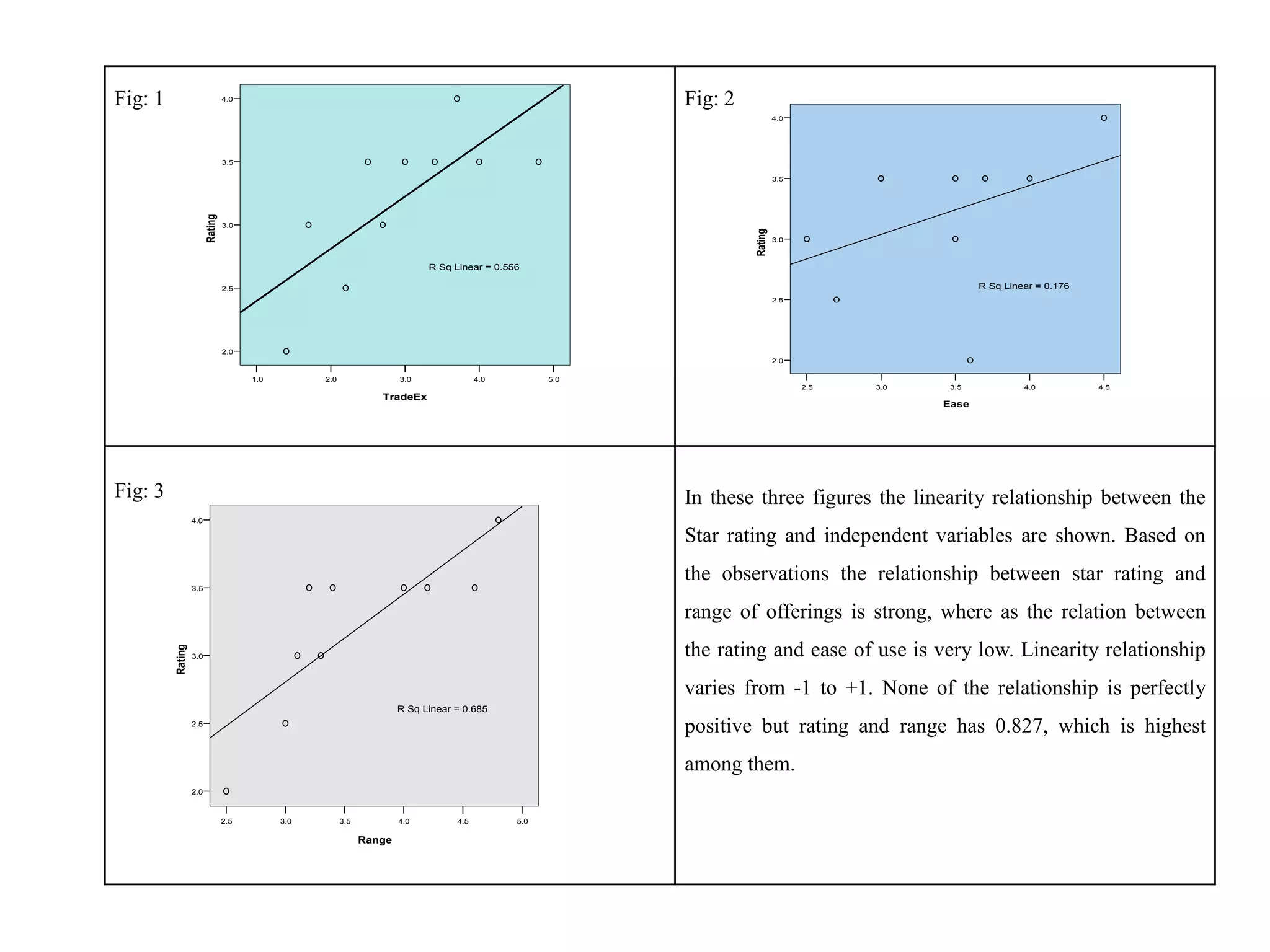
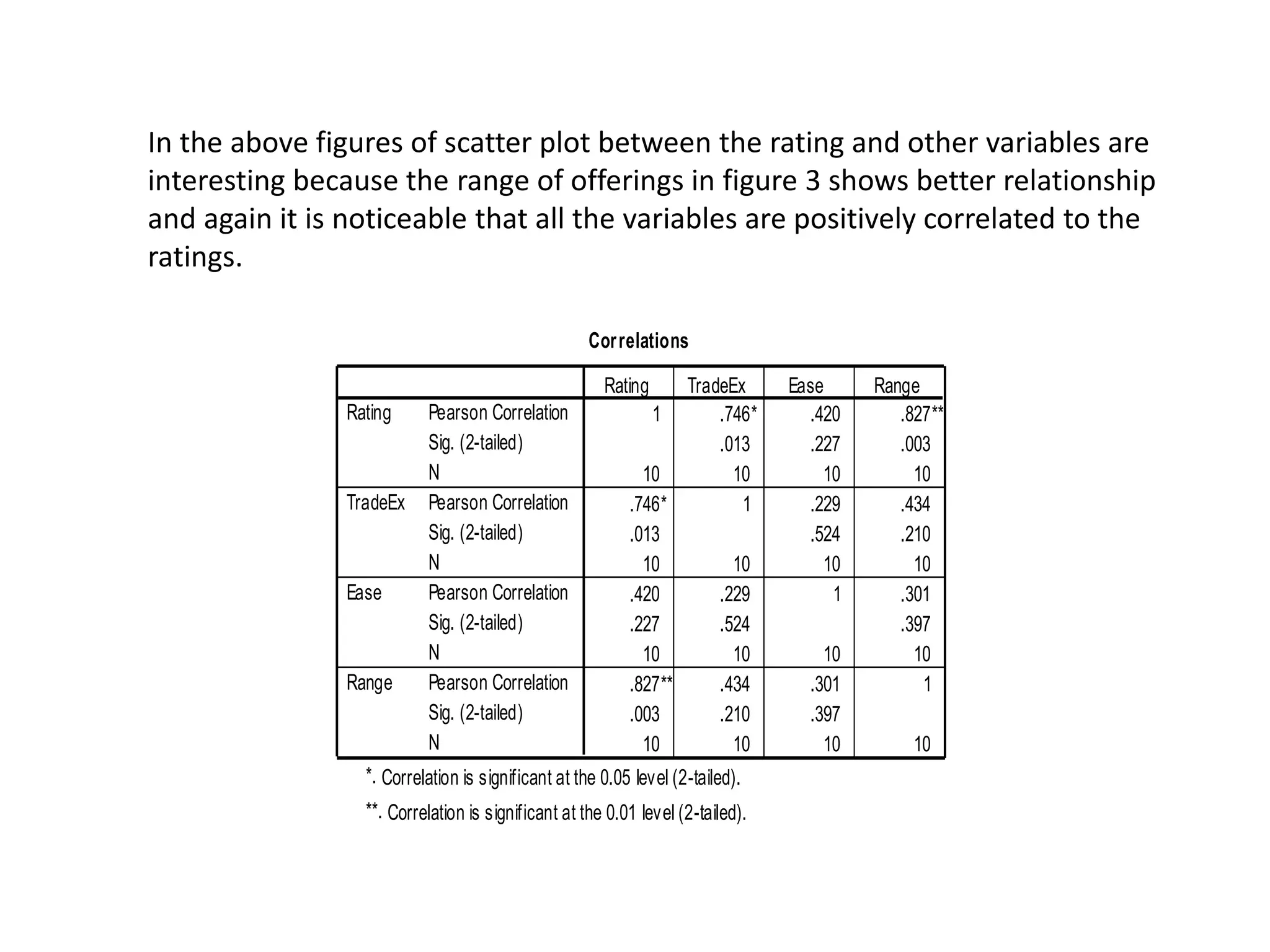
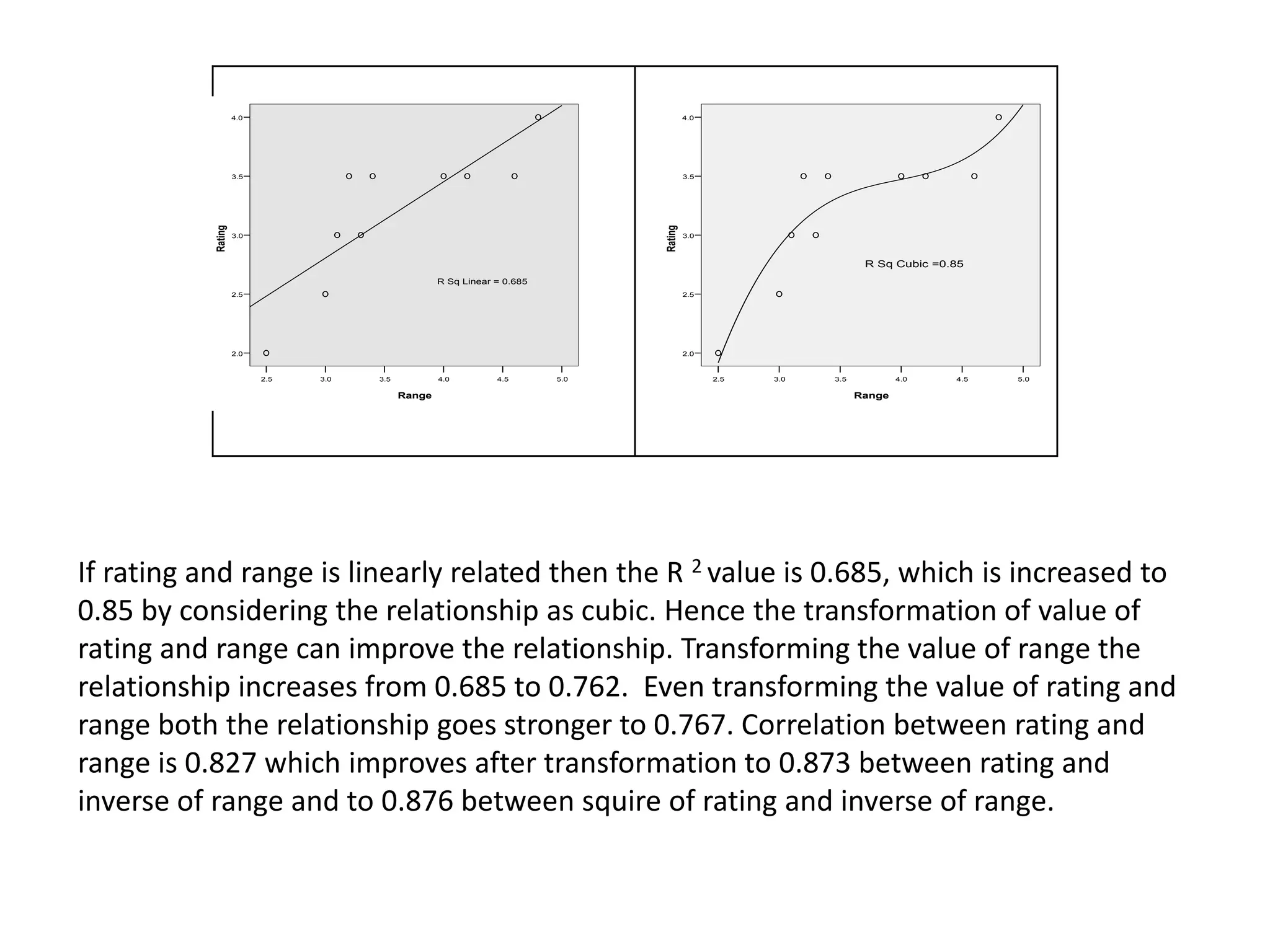
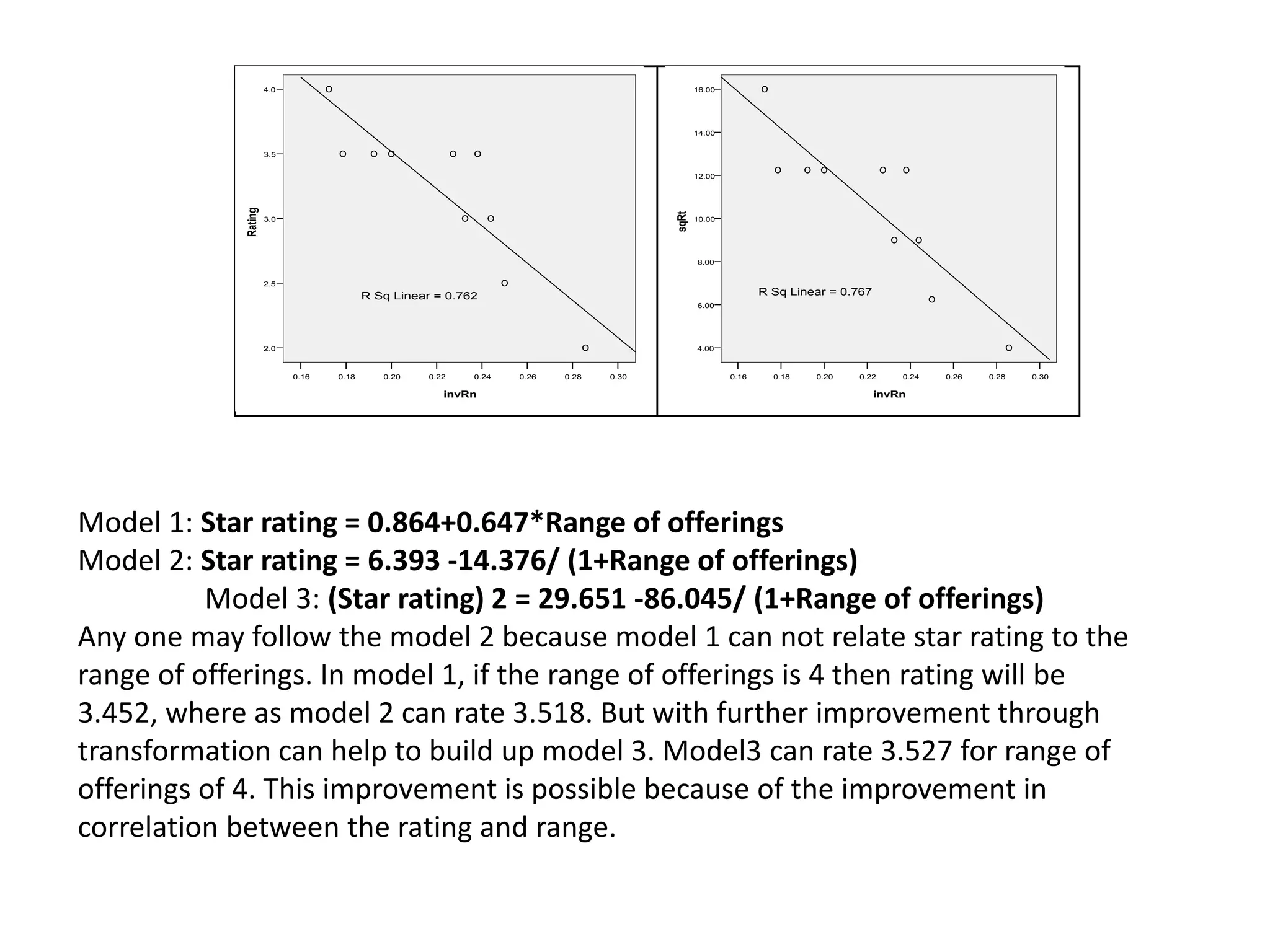
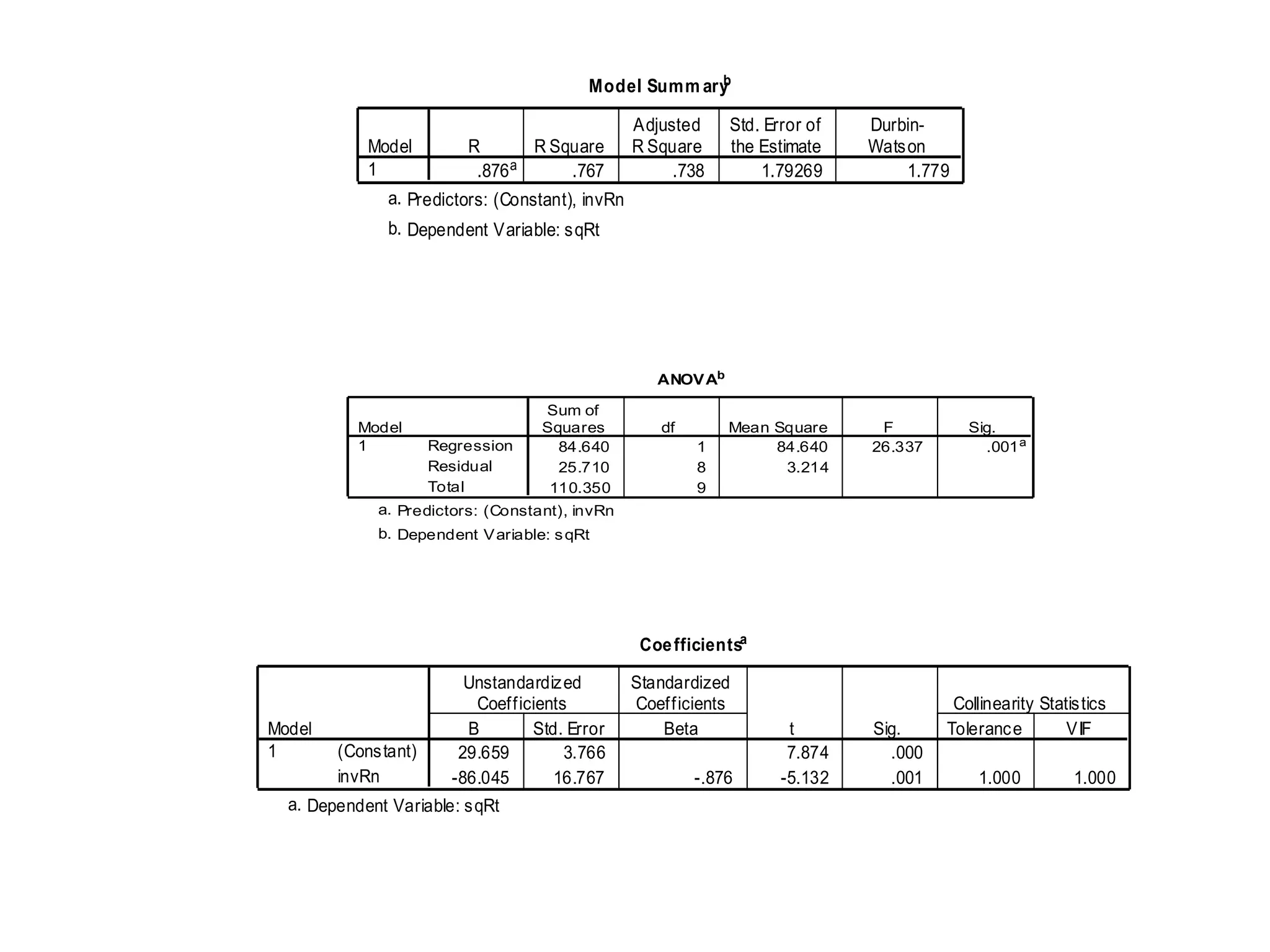
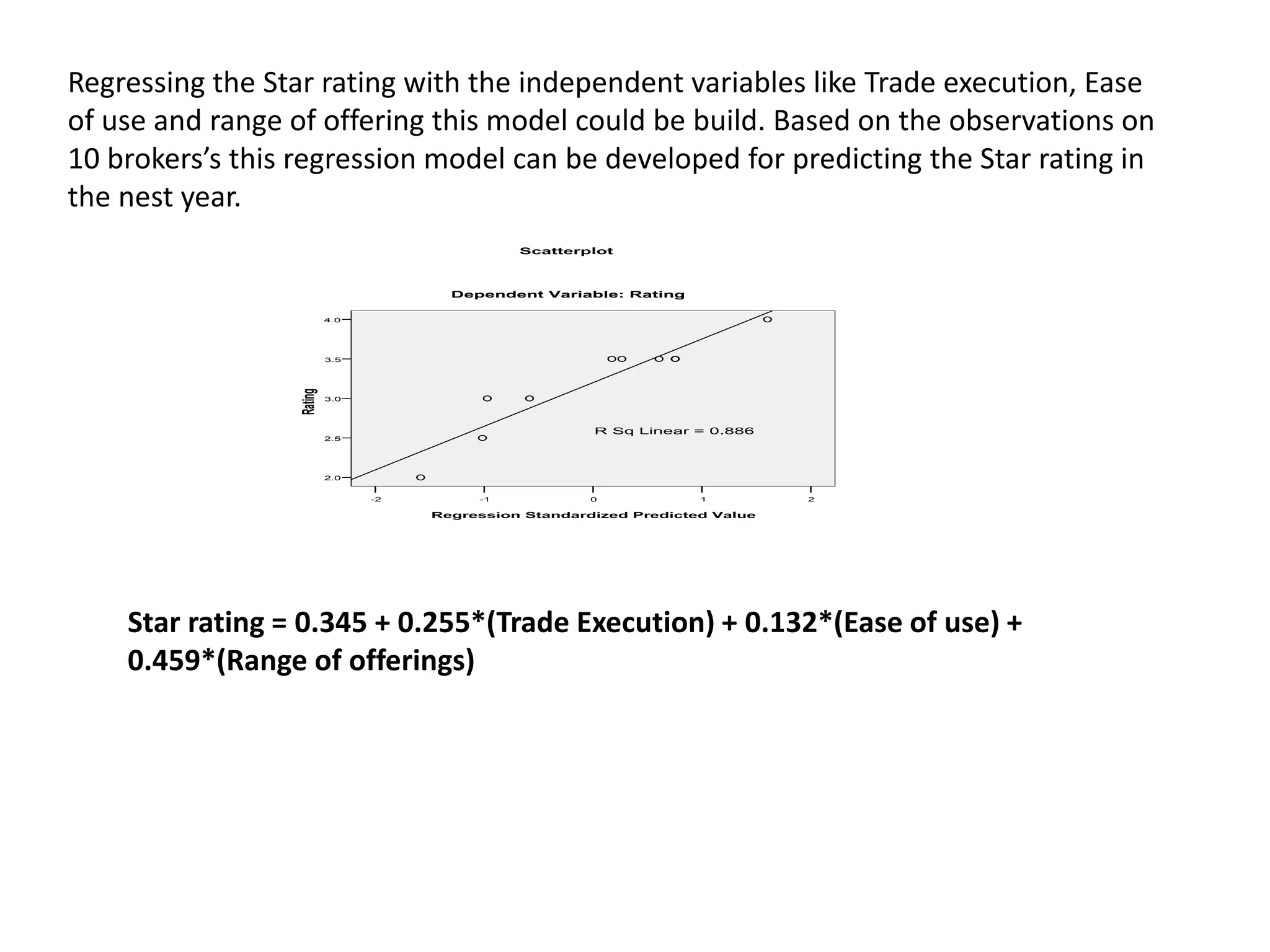
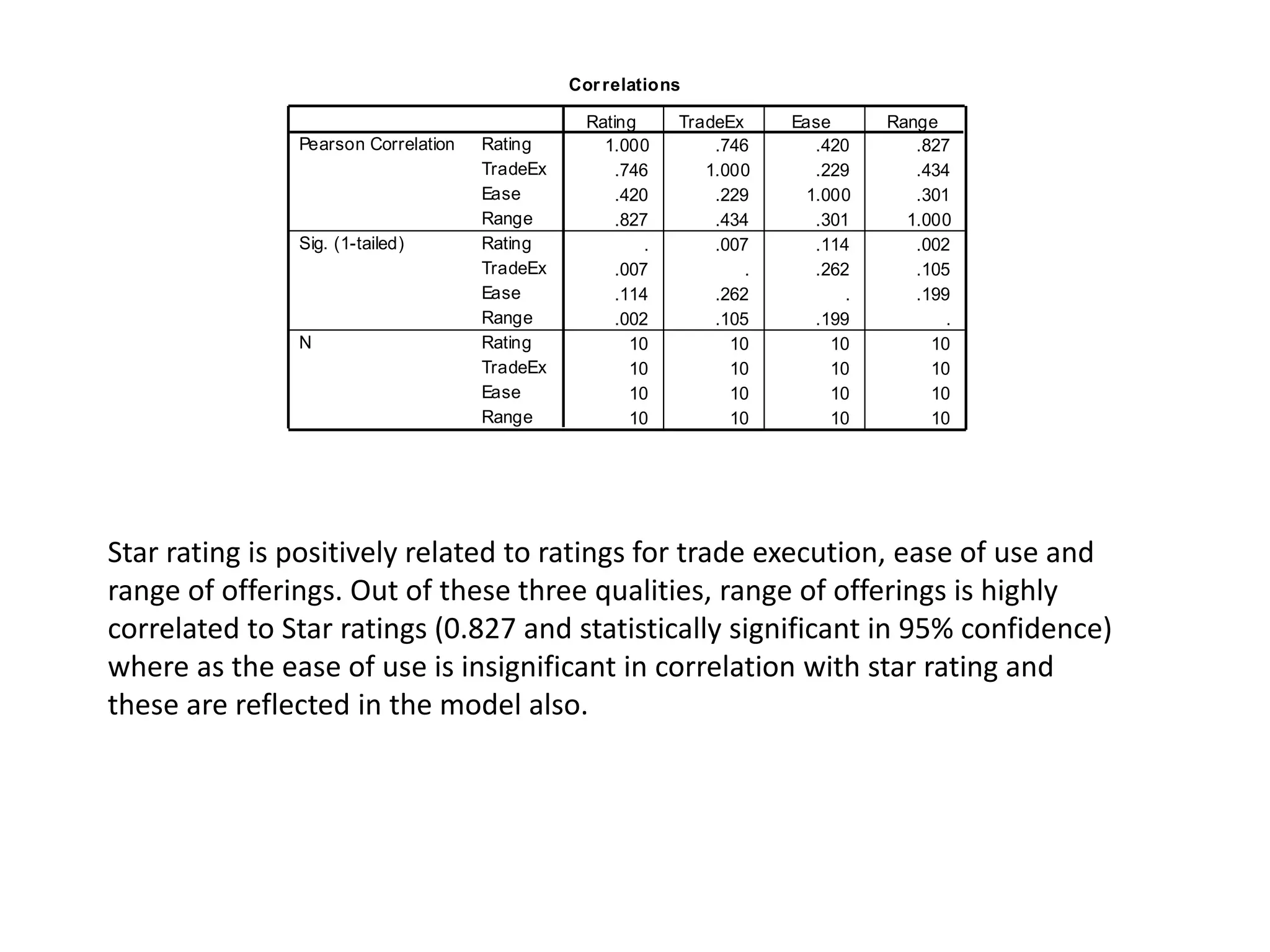
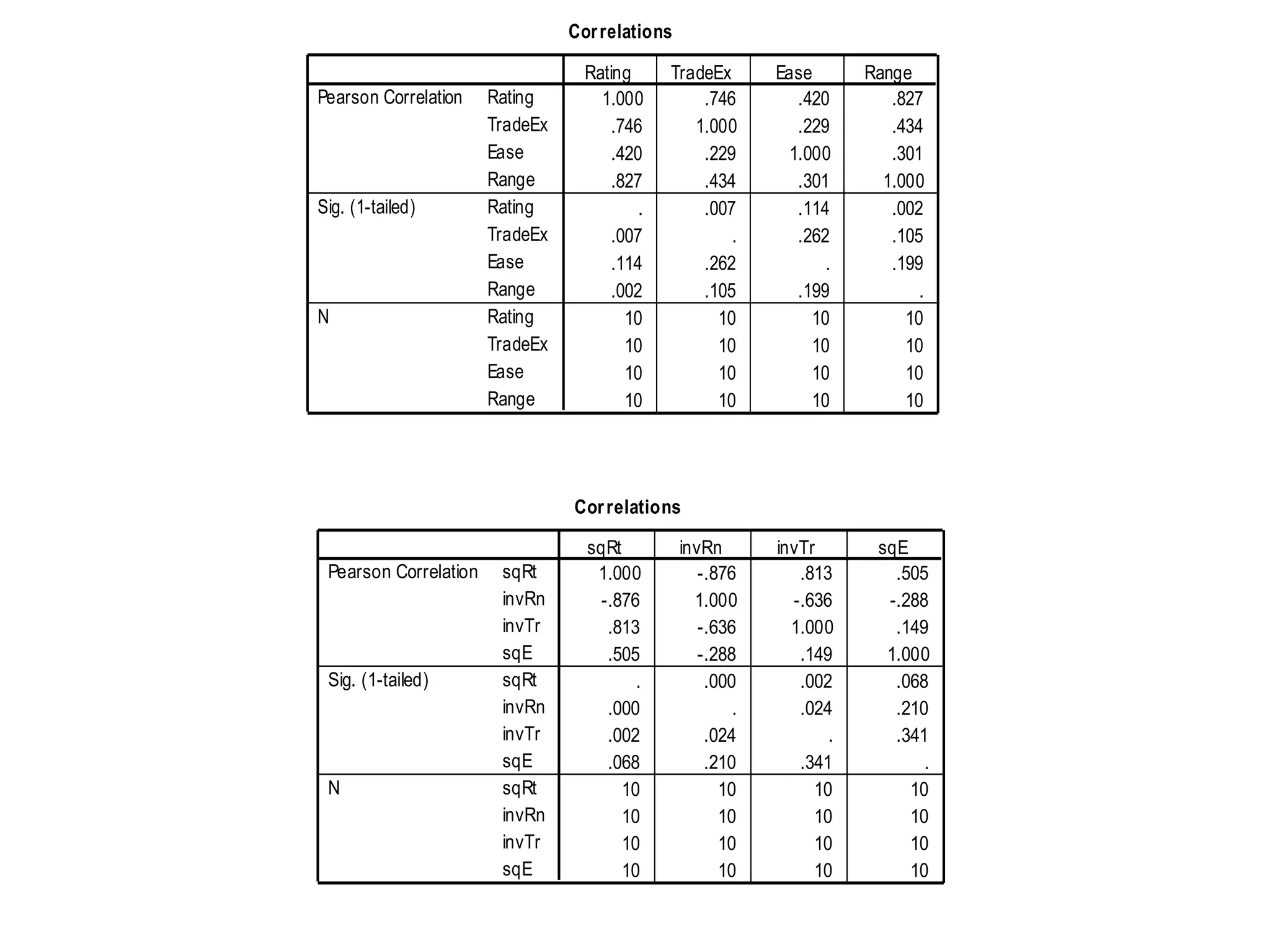
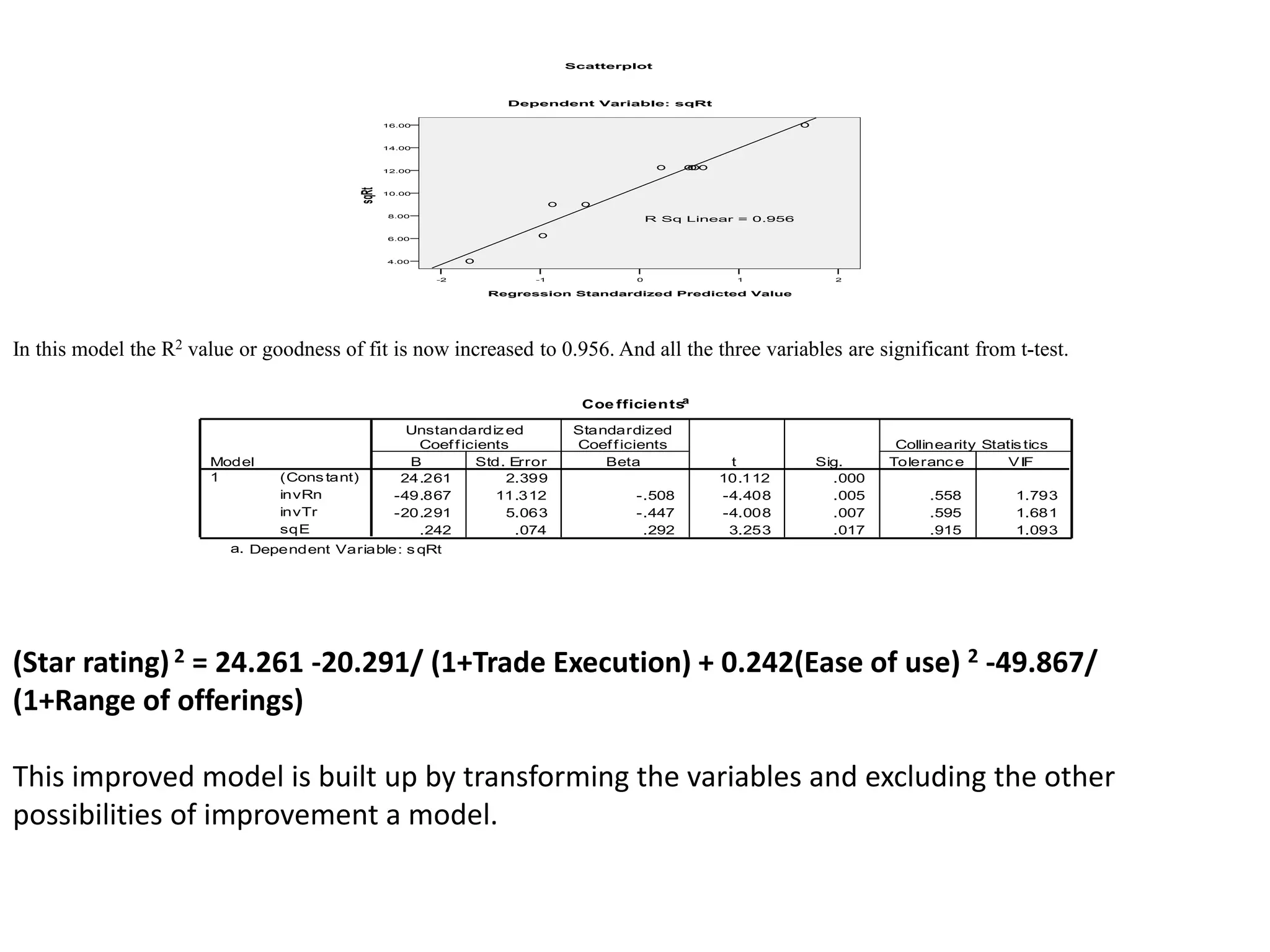
The document describes research on predicting future ratings of companies rated by broker firms. Several regression models are analyzed with the star rating as the dependent variable and variables like trade execution, ease of use, and range of offerings as independent variables. The best-fitting model has an R-squared value of 0.956, indicating it accounts for over 95% of the variation in star ratings. This model relates the square of the star rating to transformed versions of the independent variables.

1. http://stochasticanalytic.com/research/
PREDICTION OF FUTURE RATINGS OF COMPANIES, THOSE ARE
RATED BY BROKER FIRMS

2. Fig: 1 Fig: 2
Fig: 3 In these three figures the linearity relationship between the
Star rating and independent variables are shown. Based on
the observations the relationship between star rating and
range of offerings is strong, where as the relation between
the rating and ease of use is very low. Linearity relationship
varies from -1 to +1. None of the relationship is perfectly
positive but rating and range has 0.827, which is highest
among them.
5.04.03.02.01.0
TradeEx
4.0
3.5
3.0
2.5
2.0
Rating
R Sq Linear = 0.556
4.54.03.53.02.5
Ease
4.0
3.5
3.0
2.5
2.0
Rating
R Sq Linear = 0.176
5.04.54.03.53.02.5
Range
4.0
3.5
3.0
2.5
2.0
Rating
R Sq Linear = 0.685

3. In the above figures of scatter plot between the rating and other variables are
interesting because the range of offerings in figure 3 shows better relationship
and again it is noticeable that all the variables are positively correlated to the
ratings.
Correlations
1 .746* .420 .827**
.013 .227 .003
10 10 10 10
.746* 1 .229 .434
.013 .524 .210
10 10 10 10
.420 .229 1 .301
.227 .524 .397
10 10 10 10
.827** .434 .301 1
.003 .210 .397
10 10 10 10
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
Rating
TradeEx
Ease
Range
Rating TradeEx Ease Range
Correlation is significant at the 0.05 level (2-tailed).*.
Correlation is significant at the 0.01 level (2-tailed).**.

4. 5.04.54.03.53.02.5
Range
4.0
3.5
3.0
2.5
2.0
Rating
R Sq Linear = 0.685
5.04.54.03.53.02.5
Range
4.0
3.5
3.0
2.5
2.0
Rating
R Sq Cubic =0.85
If rating and range is linearly related then the R 2 value is 0.685, which is increased to
0.85 by considering the relationship as cubic. Hence the transformation of value of
rating and range can improve the relationship. Transforming the value of range the
relationship increases from 0.685 to 0.762. Even transforming the value of rating and
range both the relationship goes stronger to 0.767. Correlation between rating and
range is 0.827 which improves after transformation to 0.873 between rating and
inverse of range and to 0.876 between squire of rating and inverse of range.

5. 0.300.280.260.240.220.200.180.16
invRn
4.0
3.5
3.0
2.5
2.0
Rating
R Sq Linear = 0.762
0.300.280.260.240.220.200.180.16
invRn
16.00
14.00
12.00
10.00
8.00
6.00
4.00
sqRt
R Sq Linear = 0.767
Model 1: Star rating = 0.864+0.647*Range of offerings
Model 2: Star rating = 6.393 -14.376/ (1+Range of offerings)
Model 3: (Star rating) 2 = 29.651 -86.045/ (1+Range of offerings)
Any one may follow the model 2 because model 1 can not relate star rating to the
range of offerings. In model 1, if the range of offerings is 4 then rating will be
3.452, where as model 2 can rate 3.518. But with further improvement through
transformation can help to build up model 3. Model3 can rate 3.527 for range of
offerings of 4. This improvement is possible because of the improvement in
correlation between the rating and range.

6. Model Summ aryb
.876a .767 .738 1.79269 1.779
Model
1
R R Square
Adjusted
R Square
Std. Error of
the Estimate
Durbin-
Watson
Predictors: (Constant), invRna.
Dependent Variable: sqRtb.
ANOVAb
84.640 1 84.640 26.337 .001a
25.710 8 3.214
110.350 9
Regression
Residual
Total
Model
1
Sum of
Squares df Mean Square F Sig.
Predictors: (Constant), invRna.
Dependent Variable: sqRtb.
Coefficientsa
29.659 3.766 7.874 .000
-86.045 16.767 -.876 -5.132 .001 1.000 1.000
(Constant)
invRn
Model
1
B Std. Error
Unstandardized
Coefficients
Beta
Standardized
Coefficients
t Sig. Tolerance VIF
Collinearity Statistics
Dependent Variable: sqRta.

7. Regressing the Star rating with the independent variables like Trade execution, Ease
of use and range of offering this model could be build. Based on the observations on
10 brokers’s this regression model can be developed for predicting the Star rating in
the nest year.
210-1-2
Regression Standardized Predicted Value
4.0
3.5
3.0
2.5
2.0
Rating
Dependent Variable: Rating
Scatterplot
R Sq Linear = 0.886
Star rating = 0.345 + 0.255*(Trade Execution) + 0.132*(Ease of use) +
0.459*(Range of offerings)

8. Correlations
1.000 .746 .420 .827
.746 1.000 .229 .434
.420 .229 1.000 .301
.827 .434 .301 1.000
. .007 .114 .002
.007 . .262 .105
.114 .262 . .199
.002 .105 .199 .
10 10 10 10
10 10 10 10
10 10 10 10
10 10 10 10
Rating
TradeEx
Ease
Range
Rating
TradeEx
Ease
Range
Rating
TradeEx
Ease
Range
Pearson Correlation
Sig. (1-tailed)
N
Rating TradeEx Ease Range
Star rating is positively related to ratings for trade execution, ease of use and
range of offerings. Out of these three qualities, range of offerings is highly
correlated to Star ratings (0.827 and statistically significant in 95% confidence)
where as the ease of use is insignificant in correlation with star rating and
these are reflected in the model also.

9. Model Summ aryb
.941a .886 .828 .2431 1.923
Model
1
R R Square
Adjusted
R Square
Std. Error of
the Estimate
Durbin-
Watson
Predictors: (Constant), Range, Ease, TradeExa.
Dependent Variable: Ratingb.
Higher value of R2 (0.886) of this model signifies the goodness of fit or the sample regression line is fitting well with the
observations on 10 broker platform.
ANOVAb
2.745 3 .915 15.485 .003a
.355 6 .059
3.100 9
Regression
Residual
Total
Model
1
Sum of
Squares df Mean Square F Sig.
Predictors: (Constant), Range, Ease, TradeExa.
Dependent Variable: Ratingb.
In this model the explained sum squire (ESS) is 2.745 and residual sum of squire is 0.355 which is
the reason for goodness of fit. Here R2 is equal to ESS/TSS and TSS=ESS+RSS, TSS is total sum
squire. Analysis of variance or ANOVA is useful for testing the significance of the model as Star
rating has three independent variables. In the f-test for this model the degree of freedom for
numerator is 3 because it has three independent variables and denominator has 10 – four
variables = 6, degree of freedom. Hence from the f table it could be found the standard value is
4.76. But the model has 15.485 of f-test value which is in the critical or significance zone with p
value of 0.003. As the p value is less than 0.05, hence the whole model is significant. But if the
model is looked in to detail that the easy of use has insignificant correlation with the Star rating
as well as the p value of t-test is lower than the 0.05. Hence the null hypothesis of assumption
that the coefficients are equal and zero can be rejected.

10. Coefficientsa
.345 .531 .650 .540
.255 .086 .460 2.978 .025 .801 1.249
.132 .140 .138 .944 .382 .897 1.114
.459 .123 .586 3.722 .010 .768 1.302
(Constant)
TradeEx
Ease
Range
Model
1
B Std. Error
Unstandardized
Coefficients
Beta
Standardized
Coefficients
t Sig. Tolerance VIF
Collinearity Statistics
Dependent Variable: Ratinga.
Three independent variables have standard t value of 1.943 at the 6 degree of freedom. In
this model trade execution and range of offerings have t-test value of 2.978 and 3.722,
which is higher than the 1.943 or p value is lower than 0.05. Hence for these two variables
the hypothesis of considering the coefficient with zero value can be rejected.
Star rating = 0.345 + 0.255*(Trade Execution) + 0.132*(Ease of use) + 0.459*(Range of
offerings)

11. In this model if the trade execution drops by -2 then the effect on star rating will
be – (0.255*2) = -0.51. Or the star rating will be decreased by 0.51.
Where as the decrease in range of offerings by -3 will impact on Star rating by
0.459*3= 1.377. Or the star rating will be decreased by 1.337.
Change in range of offerings will be impacted more for this model.
This regression model has fewer diseases (Low Multicollinerity as VIF is nearly 1,
no auto regression as DW is nearly 2) but can be improved by
Increasing the sample size
Inclusion of more variables
Transforming variables.
Transforming all four variables it can be observed that the correlation is
significantly improved.

12. Correlations
1.000 .746 .420 .827
.746 1.000 .229 .434
.420 .229 1.000 .301
.827 .434 .301 1.000
. .007 .114 .002
.007 . .262 .105
.114 .262 . .199
.002 .105 .199 .
10 10 10 10
10 10 10 10
10 10 10 10
10 10 10 10
Rating
TradeEx
Ease
Range
Rating
TradeEx
Ease
Range
Rating
TradeEx
Ease
Range
Pearson Correlation
Sig. (1-tailed)
N
Rating TradeEx Ease Range
Correlations
1.000 -.876 .813 .505
-.876 1.000 -.636 -.288
.813 -.636 1.000 .149
.505 -.288 .149 1.000
. .000 .002 .068
.000 . .024 .210
.002 .024 . .341
.068 .210 .341 .
10 10 10 10
10 10 10 10
10 10 10 10
10 10 10 10
sqRt
invRn
invTr
sqE
sqRt
invRn
invTr
sqE
sqRt
invRn
invTr
sqE
Pearson Correlation
Sig. (1-tailed)
N
sqRt invRn invTr sqE

13. 210-1-2
Regression Standardized Predicted Value
16.00
14.00
12.00
10.00
8.00
6.00
4.00
sqRt
Dependent Variable: sqRt
Scatterplot
R Sq Linear = 0.956
In this model the R2 value or goodness of fit is now increased to 0.956. And all the three variables are significant from t-test.
Coe fficientsa
24.261 2.399 10.112 .000
-49.867 11.312 -.508 -4.408 .005 .558 1.793
-20.291 5.063 -.447 -4.008 .007 .595 1.681
.242 .074 .292 3.253 .017 .915 1.093
(Cons tant)
invRn
invTr
sqE
Model
1
B Std. Error
Unstandardiz ed
Coefficients
Beta
Standardized
Coefficients
t Sig. Toleranc e VIF
Collinearity Statis tics
Dependent Variable: s qRta.
(Star rating)2 = 24.261 -20.291/ (1+Trade Execution) + 0.242(Ease of use) 2 -49.867/
(1+Range of offerings)
This improved model is built up by transforming the variables and excluding the other
possibilities of improvement a model.