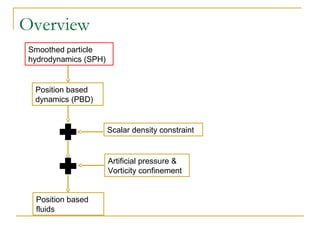
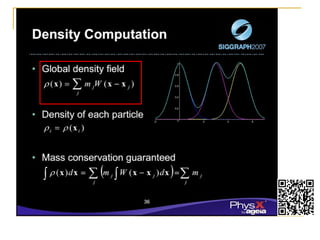
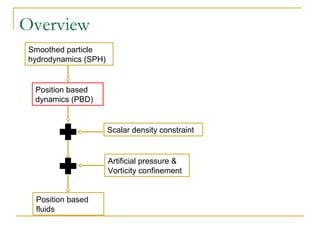
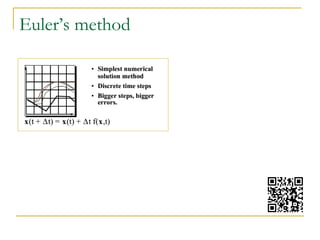
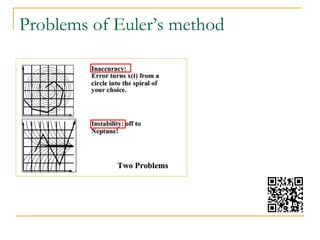
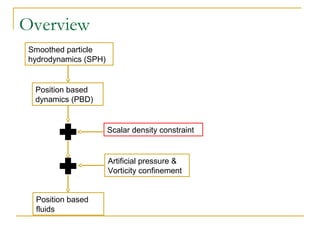
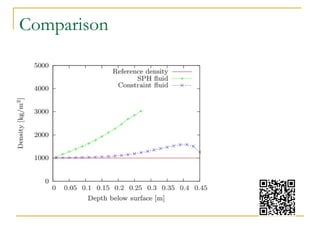
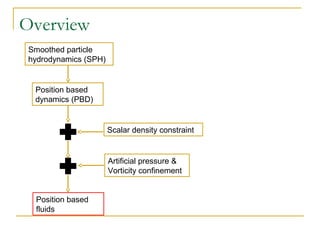
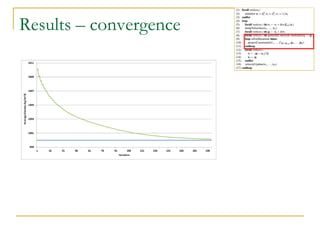
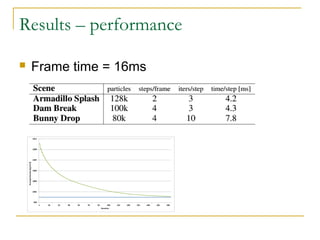
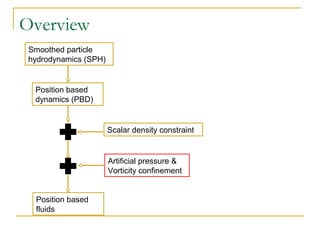
This document summarizes a technique called position based fluids. It describes how smoothed particle hydrodynamics (SPH) and position based dynamics (PBD) are used. SPH uses kernel functions to compute density from particle positions. PBD iteratively solves constraints to update positions implicitly. The technique uses a scalar density constraint based on target density. It also applies artificial pressure and vorticity confinement forces. It can simulate fluids with 128k particles at 16ms per frame using this position based approach.