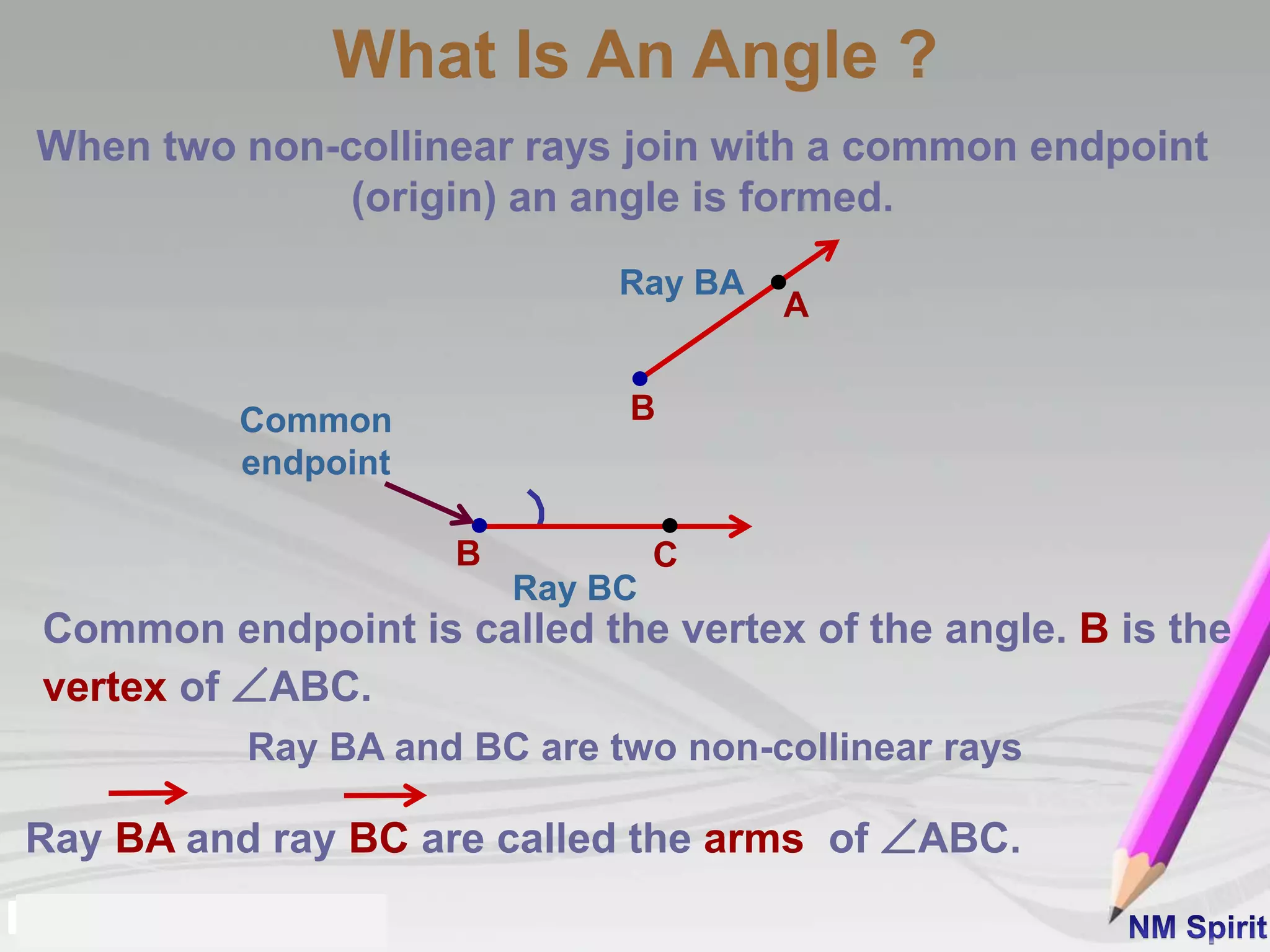
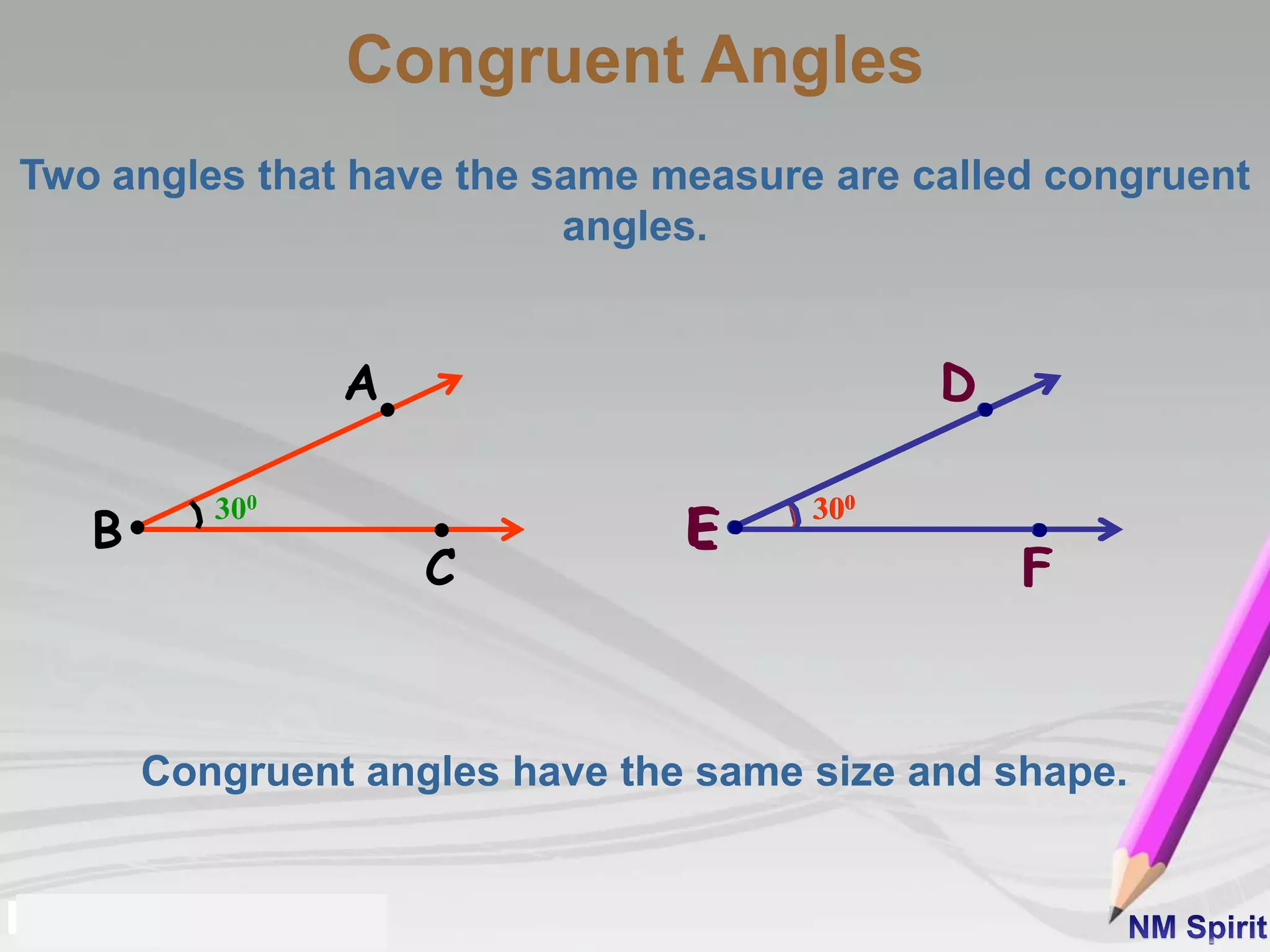
This document defines and explains various geometric terms related to lines and angles: - A line is a straight path extending indefinitely in both directions without endpoints. A line segment is a part of a line with two endpoints. A ray is a line segment extending indefinitely in one direction from an endpoint. - An angle is formed by two rays with a common endpoint. The common endpoint is called the vertex. The rays are the arms of the angle. Angles can be acute, right, or obtuse depending on their measure. 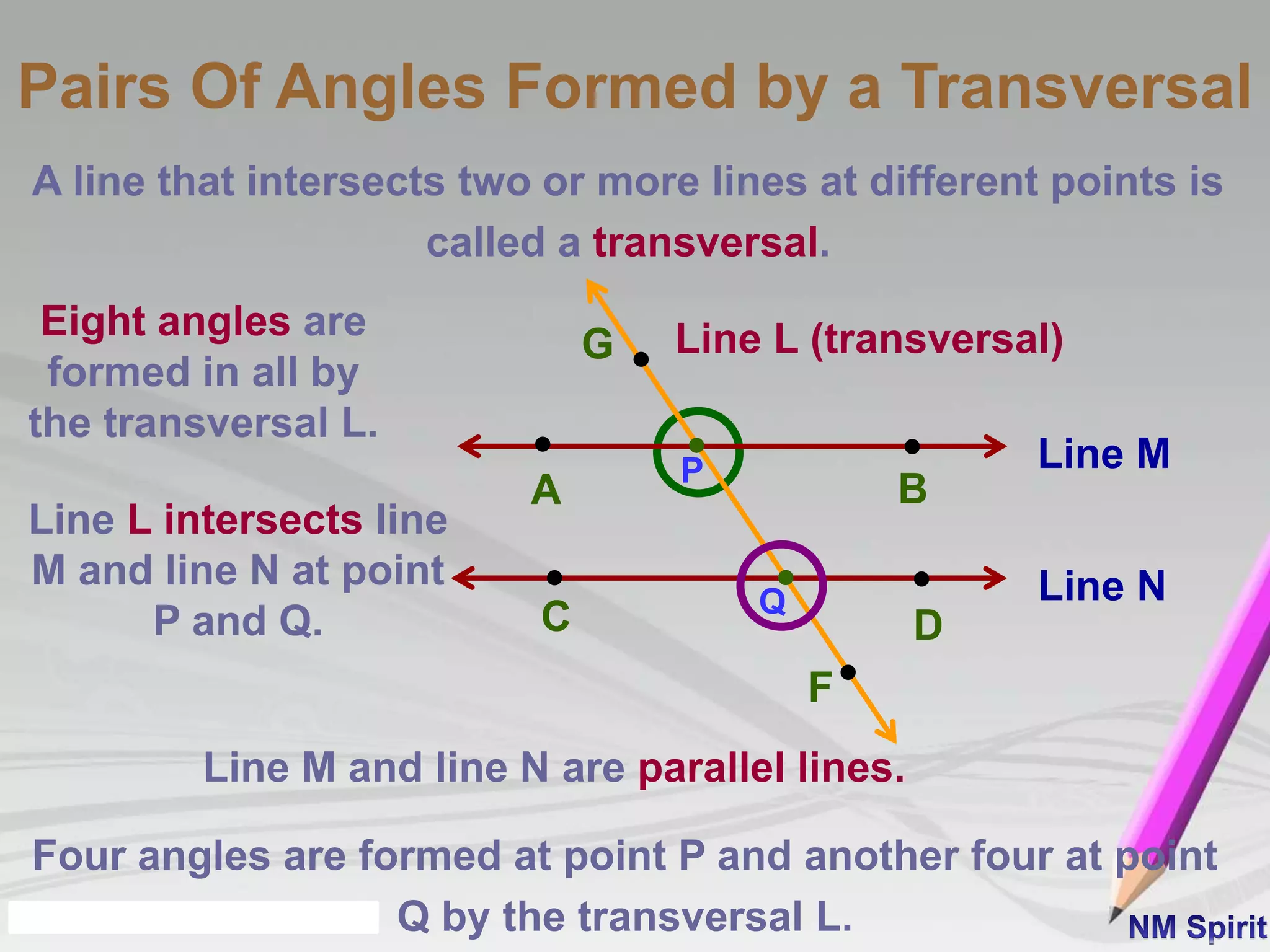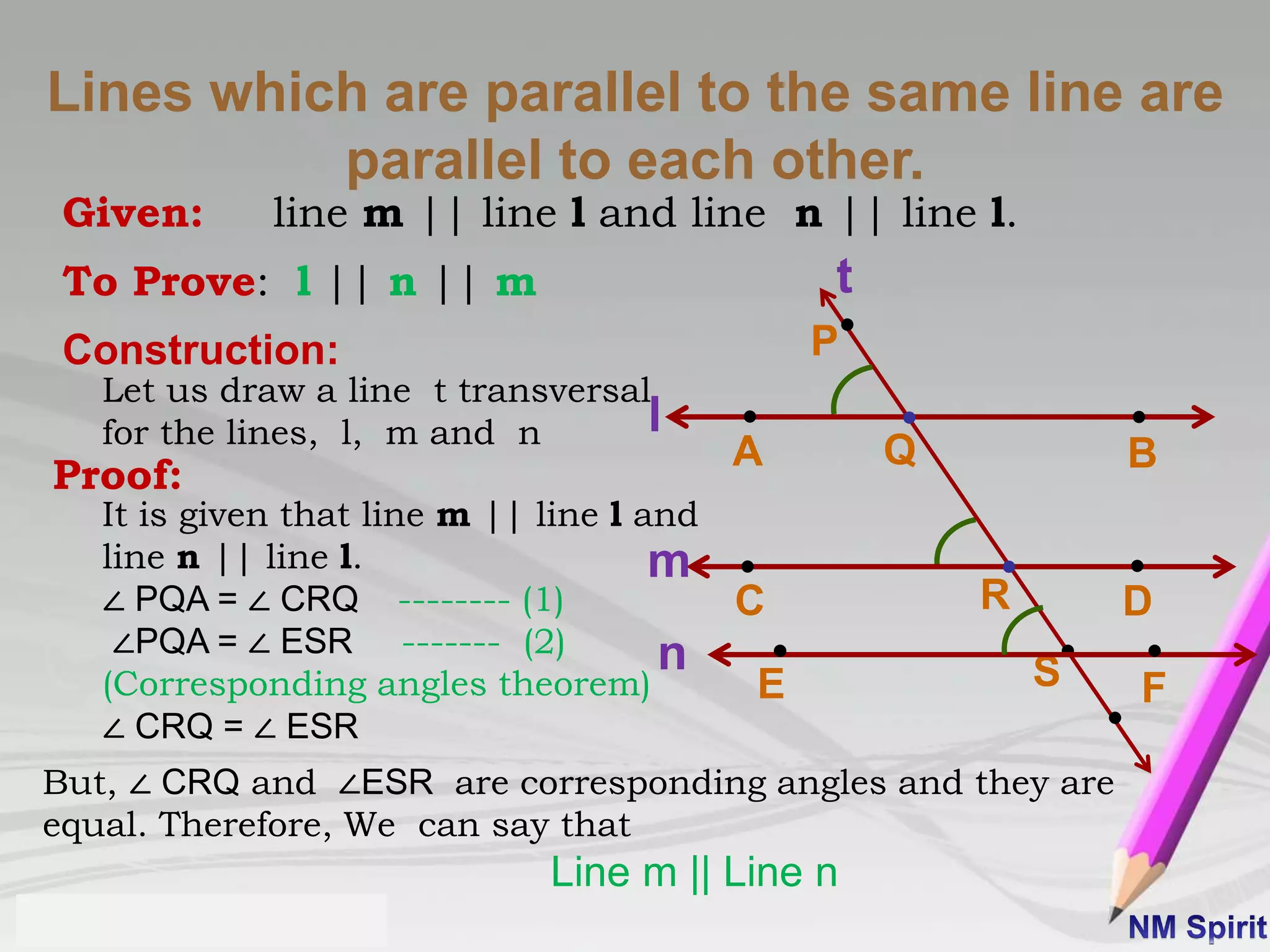- Pairs of angles include adjacent angles with a common vertex and ray, vertically opposite angles formed by intersecting lines, complementary angles with a sum of 90 degrees, and supplementary angles with a sum of 180

1. Line
s &Angle
s
By - NM Spirit
T- 901-568-0202
Email-
nm.sspirit@gmail.com

2. Point
An exact location on a plane is
called a point.
Line
Line
segment
Ray
A straight path on a plane,
extending in both directions
with no endpoints, is called a
line.
A part of a line that has two
endpoints and thus has a
definite length is called a line
segment.
A line segment extended
indefinitely in one direction
is called a ray.
Recap Geometrical Terms

4. RAY: A part of a line, with one endpoint, that continues
without end in one direction
LINE: A straight path extending in both directions with no
endpoints
LINE SEGMENT: A part of a line that includes two
points, called endpoints, and all the points between
them

5. INTERSECTING LINES: Lines that cross
PARALLEL LINES: Lines that never cross and are always
the same distance apart

6. Common
endpoint
B C
B
A
Ray BC
Ray BA
Ray BA and BC are two non-collinear rays
When two non-collinear rays join with a common endpoint
(origin) an angle is formed.
What Is An Angle ?
Common endpoint is called the vertex of the angle. B is the
vertex of ABC.
Ray BA and ray BC are called the arms of ABC.

7. To name an angle, we name any point on one ray, then the
vertex, and then any point on the other ray.
For example: ABC or CBA
We may also name this angle only by the single letter of the
vertex, for example B.
A
B
C
Naming An Angle

8. An angle divides the points on the plane into three regions:
A
B
C
F
R
P
T
X
Interior And Exterior Of An Angle
• Points lying on the angle
(An angle)
• Points within the angle
(Its interior portion. )
• Points outside the angle
(Its exterior portion. )

9. Right Angle:
An angle that forms a
square corner
Acute Angle:
An angle less
than a right angle
Obtuse Angle:
An angle greater
than a right angle

10. Two angles that have the same measure are called congruent
angles.
Congruent angles have the same size and shape.
A
B
C
300
D
E
F
300
D
E
F
300
Congruent Angles

11. Pairs Of Angles : Types
• Adjacent angles
• Vertically opposite angles
• Complimentary angles
• Supplementary angles
• Linear pairs of angles

12. Adjacent Angles
Two angles that have a common vertex and a common ray
are called adjacent angles.
C
D
B
A
Common ray
Common vertex
Adjacent Angles ABD and DBC
Adjacent angles do not overlap each other.
D
E
F
A
B
C
ABC and DEF are not adjacent angles

13. Vertically Opposite Angles
Vertically opposite angles are pairs of angles formed by two
lines intersecting at a point.
APC = BPD
APB = CPD
A
DB
C
P
Four angles are formed at the point of intersection.
Point of intersection ‘P’ is the common vertex of the four
angles.
Vertically opposite angles are congruent.

14. If the sum of two angles is 900, then they are called
complimentary angles.
600
A
B
C
300
D
E
F
ABC and DEF are complimentary because
600 + 300 = 900
ABC + DEF
Complimentary Angles

15. If the sum of two angles is 1800 then they are called
supplementary angles.
PQR and ABC are supplementary, because
1000 + 800 = 1800
RQ
P
A
B
C
1000
800
PQR + ABC
Supplementary Angles

16. Two adjacent supplementary angles are called linear pair
of angles.
A
600 1200
PC D
600 + 1200 = 1800
APC + APD
Linear Pair Of Angles

17. A line that intersects two or more lines at different points is
called a transversal.
Line L (transversal)
BA
Line M
Line N
DC
P
Q
G
F
Pairs Of Angles Formed by a Transversal
Line M and line N are parallel lines.
Line L intersects line
M and line N at point
P and Q.
Four angles are formed at point P and another four at point
Q by the transversal L.
Eight angles are
formed in all by
the transversal L.

18. Pairs Of Angles Formed by a Transversal
• Corresponding angles
• Alternate angles
• Interior angles

19. Corresponding Angles
When two parallel lines are cut by a transversal, pairs of
corresponding angles are formed.
Four pairs of corresponding angles are formed.
Corresponding pairs of angles are congruent.
GPB = PQE
GPA = PQD
BPQ = EQF
APQ = DQF
Line M
BA
Line N
D E
L
P
Q
G
F
Line L

20. Alternate Angles
Alternate angles are formed on opposite sides of the
transversal and at different intersecting points.
Line M
BA
Line N
D E
L
P
Q
G
F
Line L
BPQ = DQP
APQ = EQP
Pairs of alternate angles are congruent.
Two pairs of alternate angles are formed.

21. The angles that lie in the area between the two parallel lines
that are cut by a transversal, are called interior angles.
A pair of interior angles lie on the same side of the
transversal.
The measures of interior angles in each pair add up to 1800.
Interior Angles
Line M
BA
Line N
D E
L
P
Q
G
F
Line L
600
1200
1200
600
BPQ + EQP = 1800
APQ + DQP = 1800

22. Theorems of
Lines and
Angles

23. If a ray stands on a line, then the sum of the
adjacent angles so formed is 180°.
PX Y
QGiven: The ray PQ stands on the line XY.
To Prove: ∠QPX + ∠YPQ = 1800
Construction: Draw PE perpendicular to XY.
Proof: ∠QPX = ∠QPE + ∠EPX
= ∠QPE + 90° ………………….. (i)
∠YPQ = ∠YPE − ∠QPE
= 90° − ∠QPE …………………. (ii)
(i) + (ii)
⇒ ∠QPX + ∠YPQ = (∠QPE + 90°) + (90° − ∠QPE)
∠QPX + ∠YPQ = 1800
Thus the theorem is proved
E

24. Vertically opposite angles are equal in
measure
To Prove :  =  C and B = D
A +  B = 1800 ………………. Straight line ‘l’
 B + C = 1800 ……………… Straight line ‘m’
  +  =  B + C
 A = C
Similarly B =
D
A
B
C
D
l
m
Proof:
Given: ‘l’ and ‘m’ be two lines intersecting at O as.
They lead to two pairs of vertically
opposite angles, namely,
(i) ∠ A and ∠ C (ii) ∠ B and ∠ D.

25. If a transversal intersects two lines such that a pair of
corresponding angles is equal, then the two lines are
parallel to each other.
Given: Transversal PS intersects parallel lines
AB and CD at points Q and R respectively.
To Prove:
∠ BQR = ∠ QRC and ∠ AQR = ∠ QRD
Proof :
∠ PQA = ∠ QRC ------------- (1) Corresponding angles
∠ PQA = ∠ BQR -------------- (2) Vertically opposite angles
from (1) and (2)
∠ BQR = ∠ QRC
Similarly, ∠ AQR = ∠ QRD. Hence the theorem is proved
BA
C D
p
S
Q
R

26. If a transversal intersects two lines such that a pair of
alternate interior angles is equal, then the two lines are
parallel.
Given: The transversal PS intersects lines AB and CD
at points Q and R respectively
where ∠ BQR = ∠ QRC.
To Prove: AB || CD
Proof:
∠ BQR = ∠ PQA --------- (1)
Vertically opposite angles
But, ∠ BQR = ∠ QRC ---------------- (2) Given
from (1) and (2),
∠ PQA = ∠ QRC
But they are corresponding angles.
So, AB || CD
BA
C D
P
S
Q
R

27. Lines which are parallel to the same line are
parallel to each other.
Given: line m || line l and line n || line l.
To Prove: l || n || m
Construction:
BA
C D
P
S
R
l
n
m
E F
Let us draw a line t transversal
for the lines, l, m and n
t
Proof:
It is given that line m || line l and
line n || line l.
∠ PQA = ∠ CRQ -------- (1)
∠PQA = ∠ ESR ------- (2)
(Corresponding angles theorem)
∠ CRQ = ∠ ESR
Q
But, ∠ CRQ and ∠ESR are corresponding angles and they are
equal. Therefore, We can say that
Line m || Line n

28. Call us for more information
91-901-568-0202