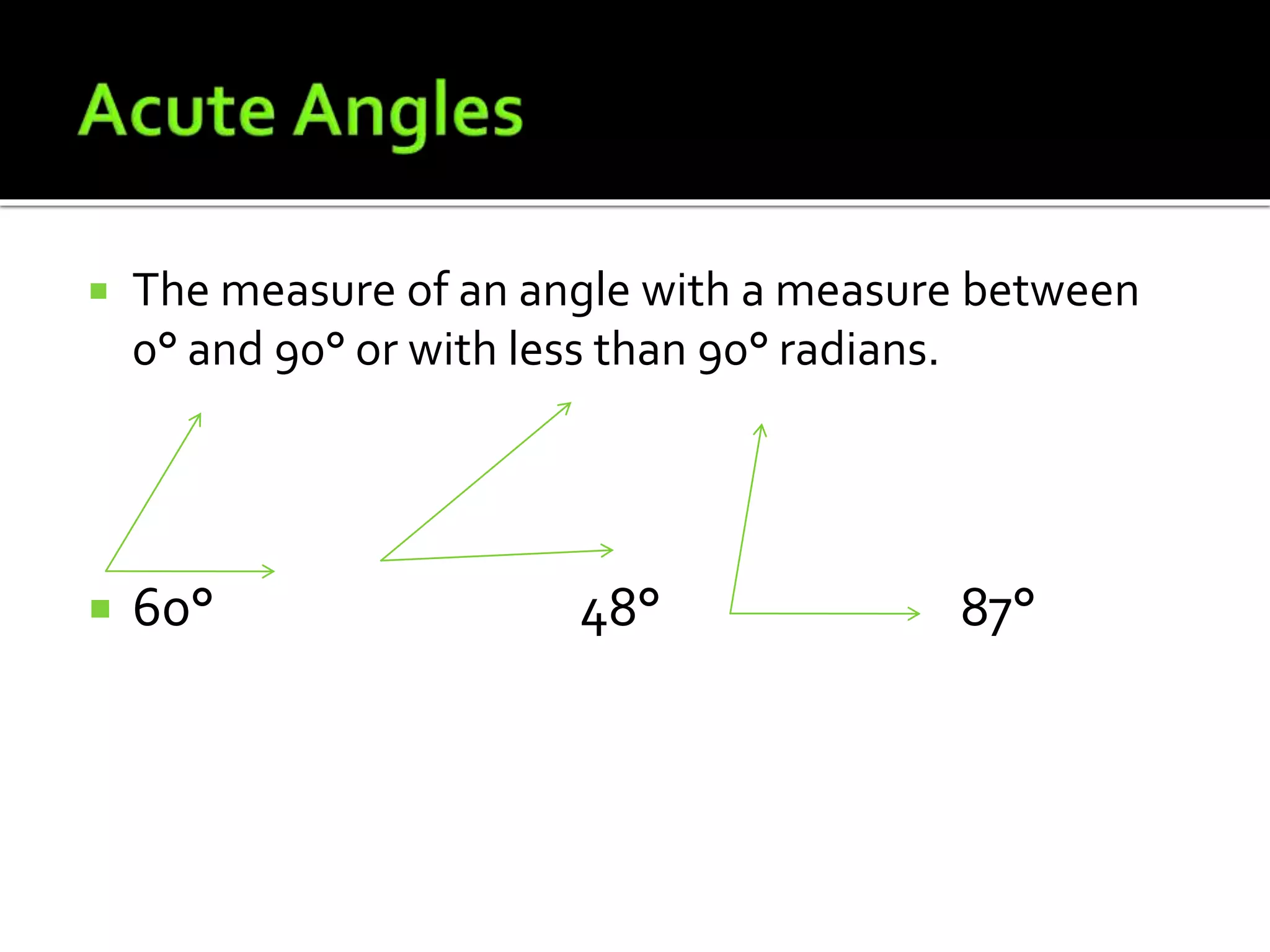
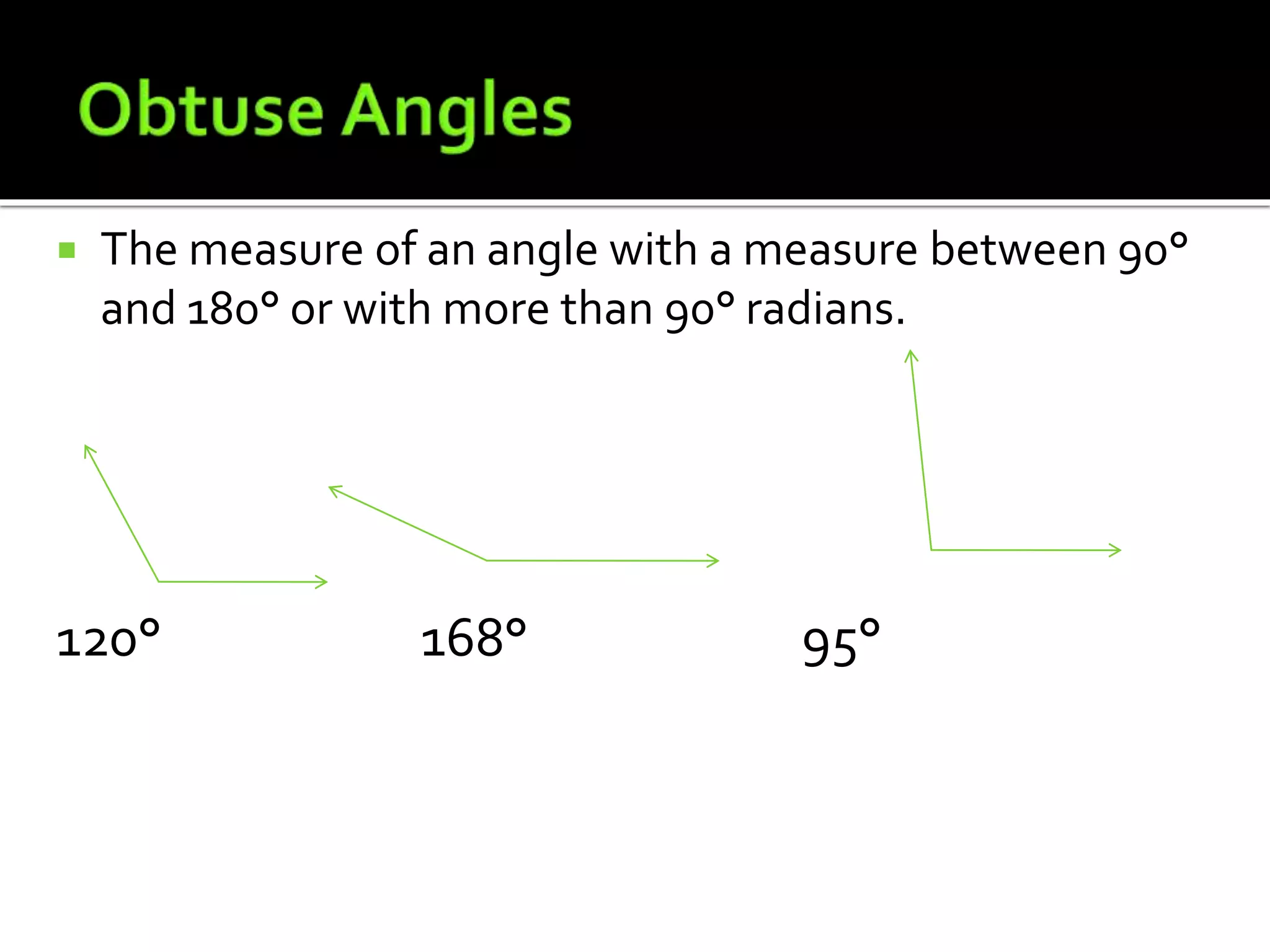
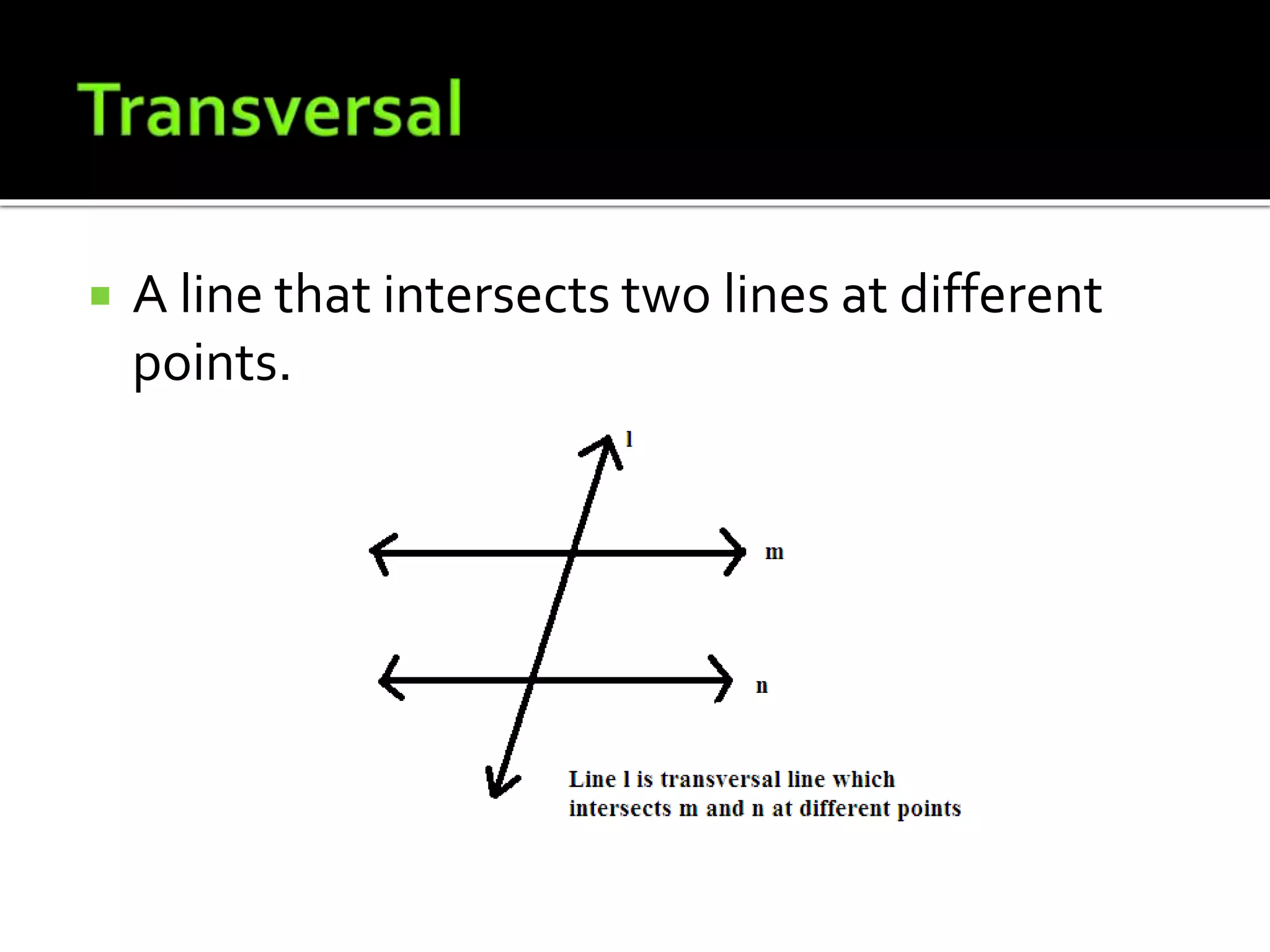
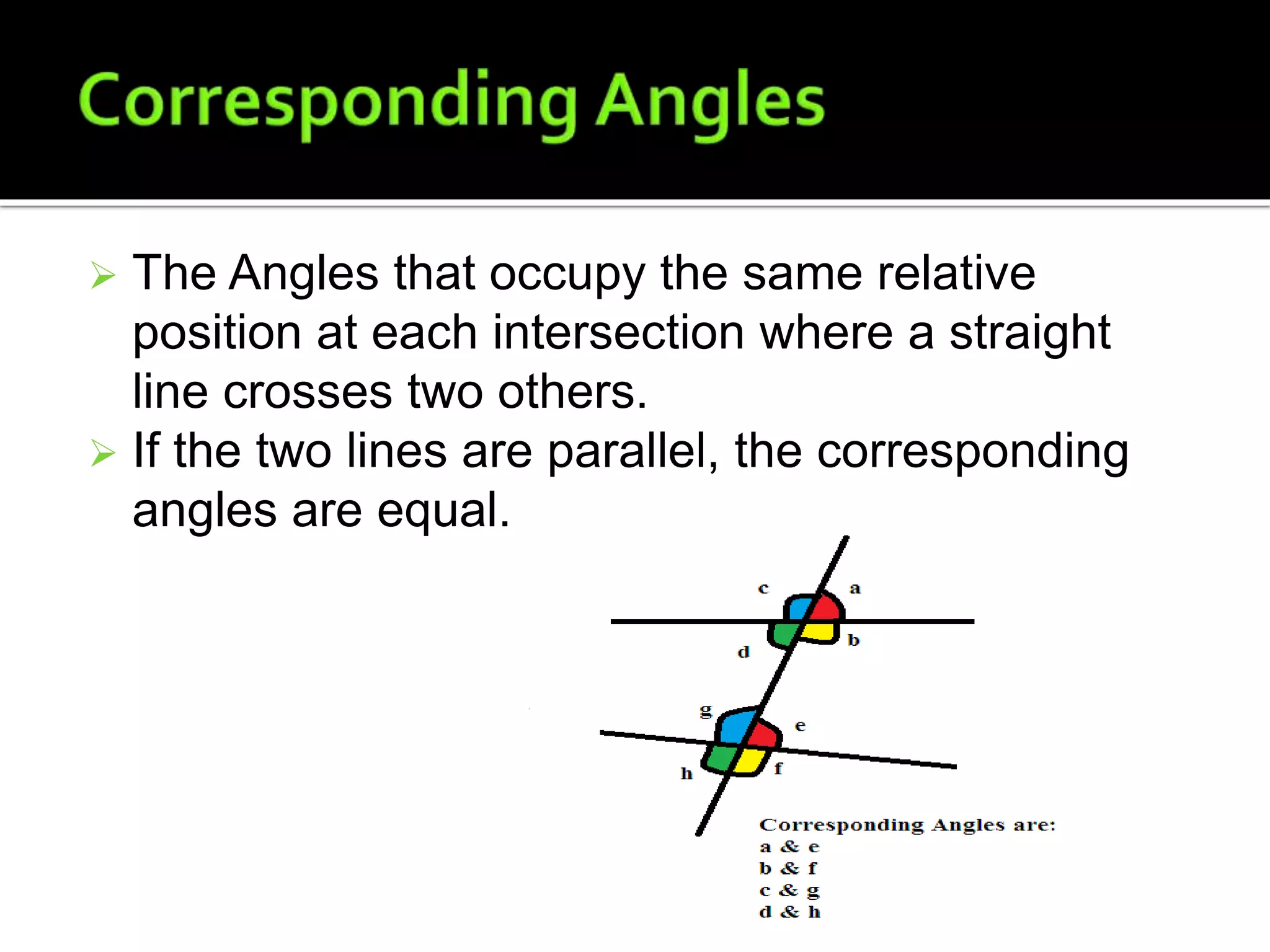
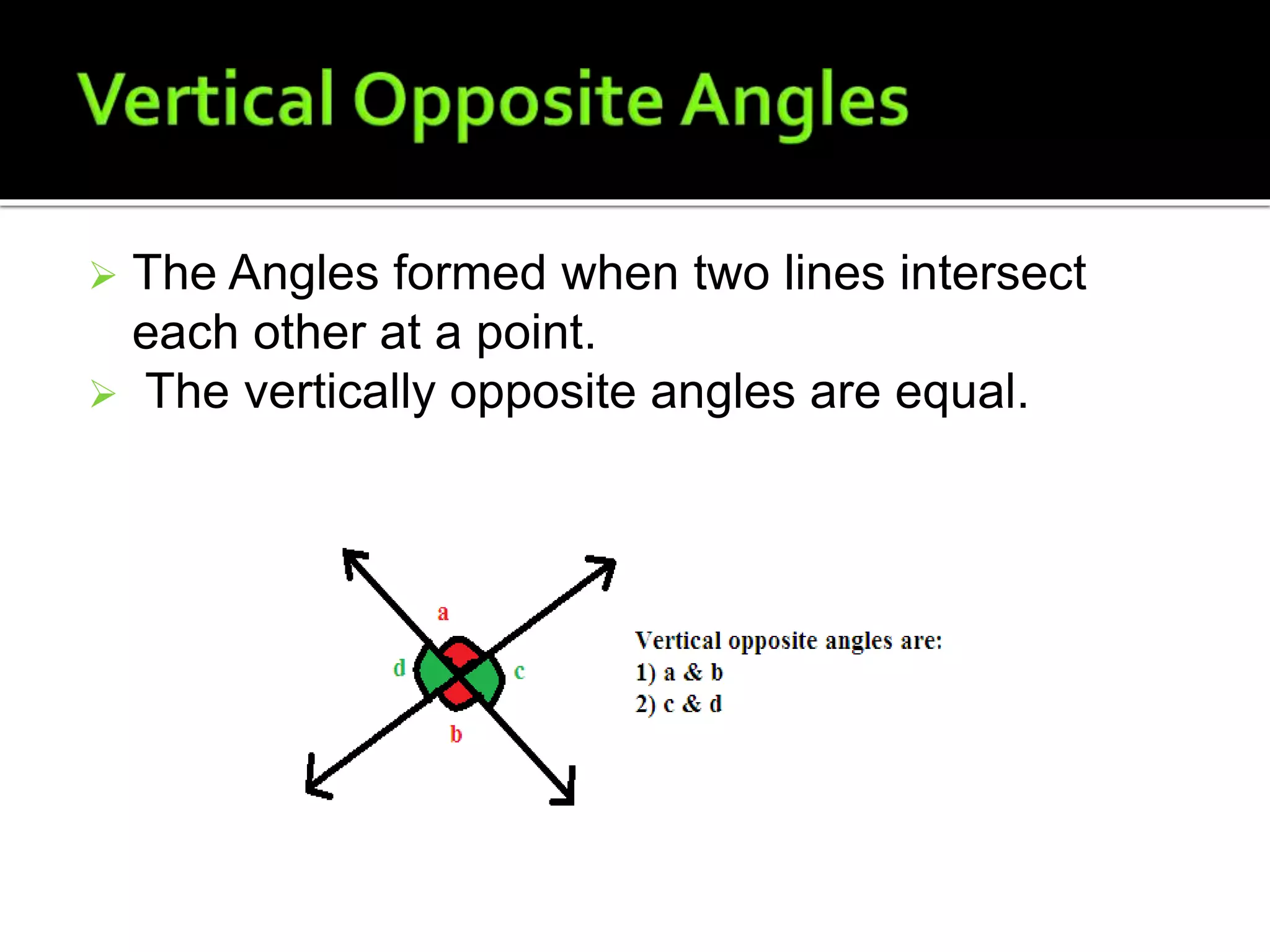
This document defines and provides examples of lines, angles, and the relationships between them. It explains that two points are needed to draw a line, which can be a line segment or ray. Lines can intersect or be parallel. Angles are formed by two rays with a common endpoint, and types of angles include acute, obtuse, right, straight, and reflex. The document also defines complementary angles, supplementary angles, adjacent angles, corresponding angles, vertical opposite angles, alternate interior angles, and alternate exterior angles.

2.  Introduction
 Lines
 Type of Lines
 Example of Lines
 Angles
 Type of Angles
 Example of Angles

3.  Lines andAngles are used in our daily life
 Lines andAngles are linked with each other
 Angles have different properties depends on
how the two lines are intersecting with each
other

4.  We require minimumTwo Points to draw a
Line
 Line can be extended through both the ends
 Line withTwo End Points is called Line-
Segment
 Line with One End Point is called Ray
 Line has No thickness and has only Length
 Three or more points lie on the same line are
calledCollinear Points

5.  There are two types of Lines :
Intersecting Lines
Non-Intersecting Lines [Parallel Lines]

6. The Lines which intersect each other at a point are
called Intersecting Lines.
Intersecting lines forms angles at their intersecting
point.
Example :
a) Fig. 1 shows two line intersecting and forming an angle
b) Fig. 2 shows two lines intersecting and forming an RightAngle, these type
of lines are called Perpendicular Lines.

7. If the distance between the two lines at each point
is same, then those lines are called Parallel Lines
Example:
The distance between Points A & C and B & D are
same

8.  An Angle is formed when two rays originate
from same end point.
 The Rays making an angle are called the arms
of Angle and the end points are calledVertex
of the angle.

9.  AcuteAngle
 Obtuse Angle
 Right Angle
 Straight Angle
 Reflex Angle
 Complementary Angles
 Supplementary Angles/Linear Pair
 Adjacent Angles
 Corresponding Angles
 Vertical Opposite angles
 Alternate Interior angles
 Alternate exterior angles

10.  The measure of an angle with a measure between
0° and 90° or with less than 90° radians.
 60° 48° 87°

11.  The measure of an angle with a measure of exact
90° is called Right Angle
90°
 This angle is formed by the perpendicular
intersection of two straight lines.

12.  The measure of an angle with a measure between 90°
and 180° or with more than 90° radians.
120° 168° 95°

13.  The measure of an angle with a measure of exact
180° is called Straight Angle
180°
 It looks like a straight line. It measures 180°
(half a revolution, or two right angles)

15.  The measure of an angle with a measure between
180° and 360° or with less than 360° radians.

16.  When two angles whose sum is 90° are called
complementary Angles.
 Angle ‘a’ and Angle ‘b’ are complementary
angles

17.  When two angles whose sum is 180° are called
Supplementary Angles or Linear Pair of Angles.
 Angle ‘a’ and Angle ‘b’ are Supplementary angles
and also they form Linear Pair.

18.  AdjacentAngles are formed when two angles
have
A common vertex
A common arm
The non-common arms are on different sides of
common arm

19.  A line that intersects two lines at different
points.

20.  The Angles that occupy the same relative
position at each intersection where a straight
line crosses two others.
 If the two lines are parallel, the corresponding
angles are equal.

21.  The Angles formed when two lines intersect
each other at a point.
 The vertically opposite angles are equal.

22.  Two angles that lie between two lines on opposite
sides of the transversal are Alternate interior angles.
 If the two lines are parallel, then Alternate interior
angles are equal.

23.  Two angles that lie outside two lines on opposite
sides of the transversal are Alternate exterior
angles.
 If the two lines are parallel, then Alternate exterior
angles are equal.