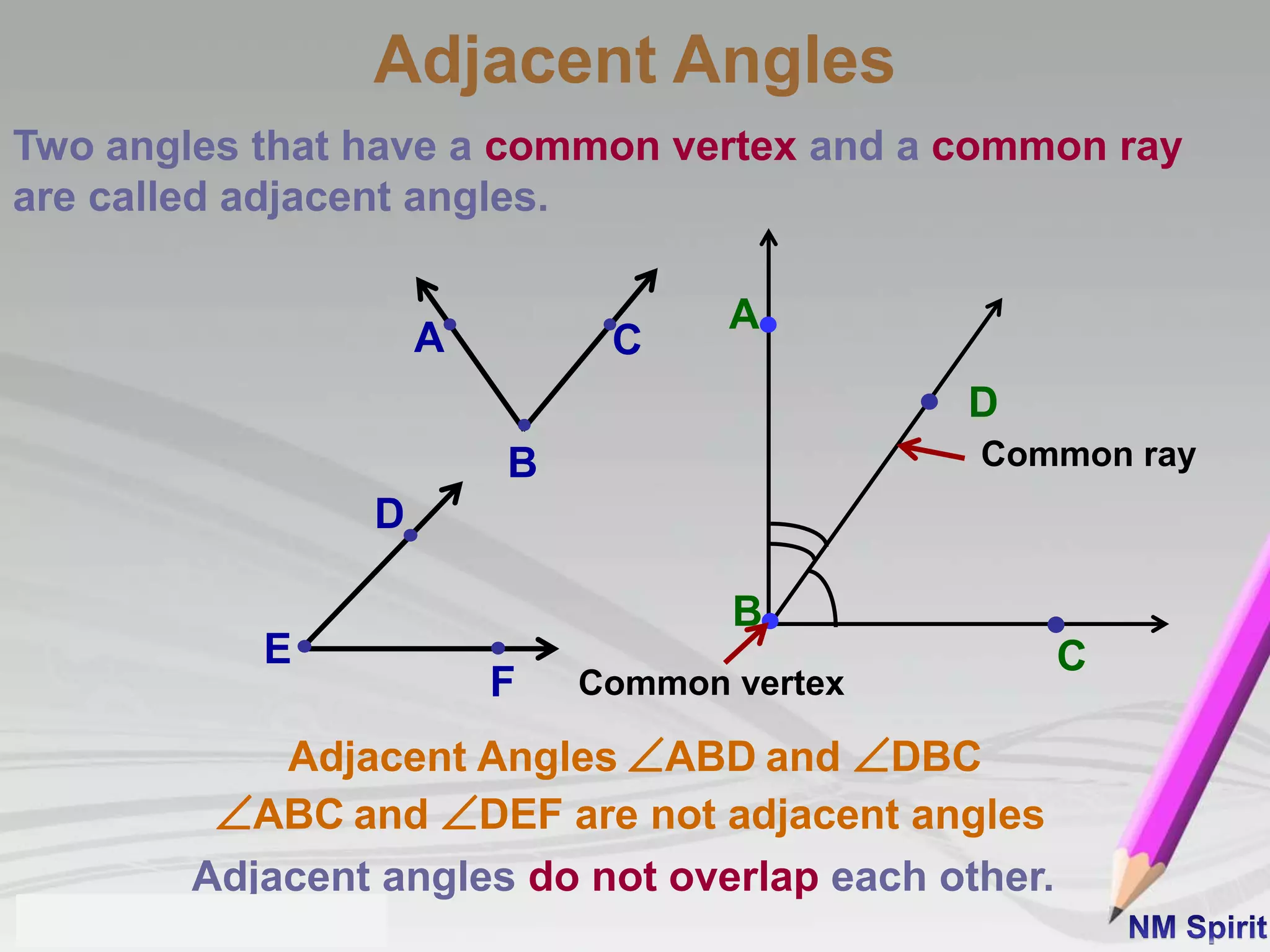
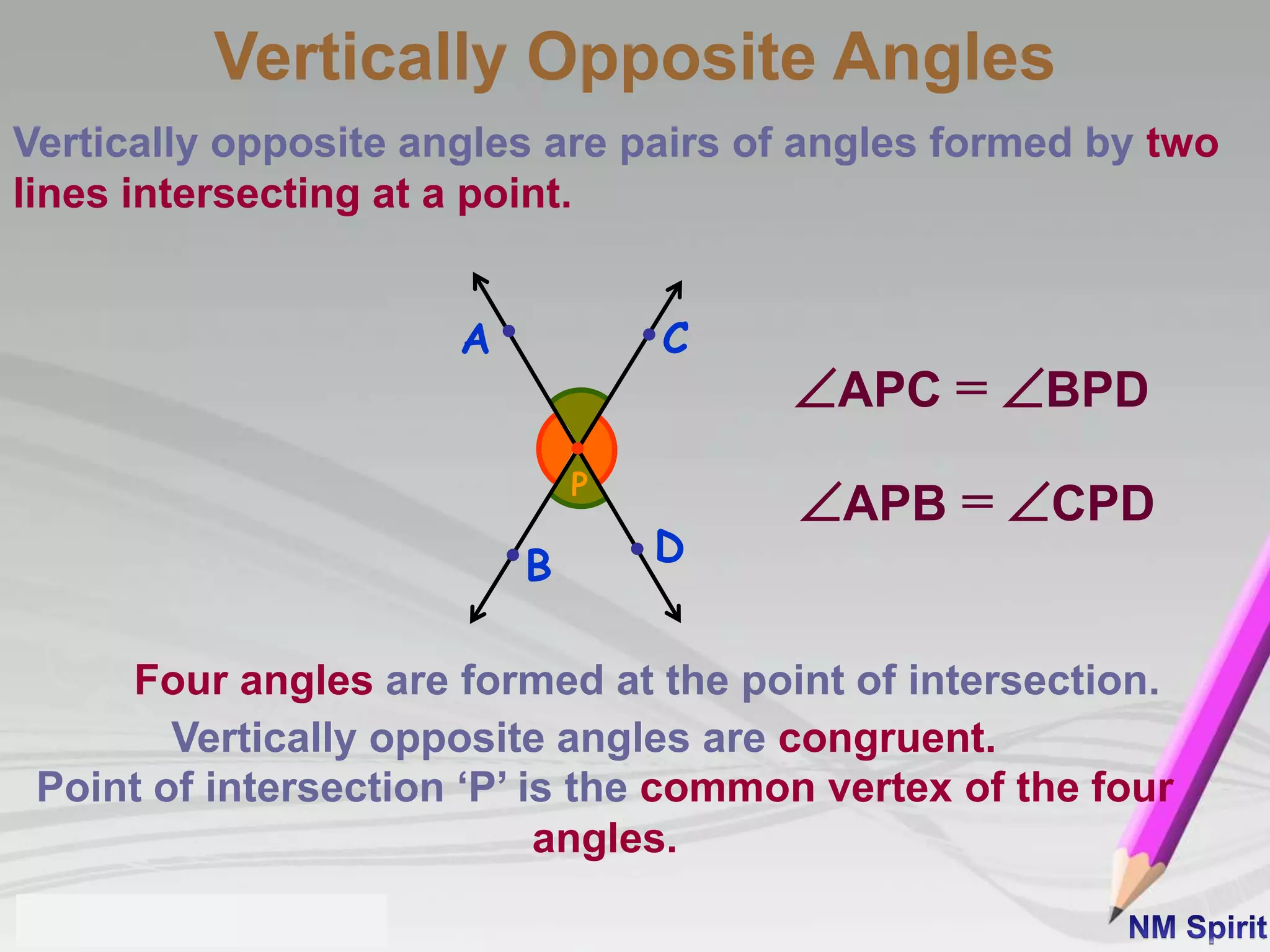
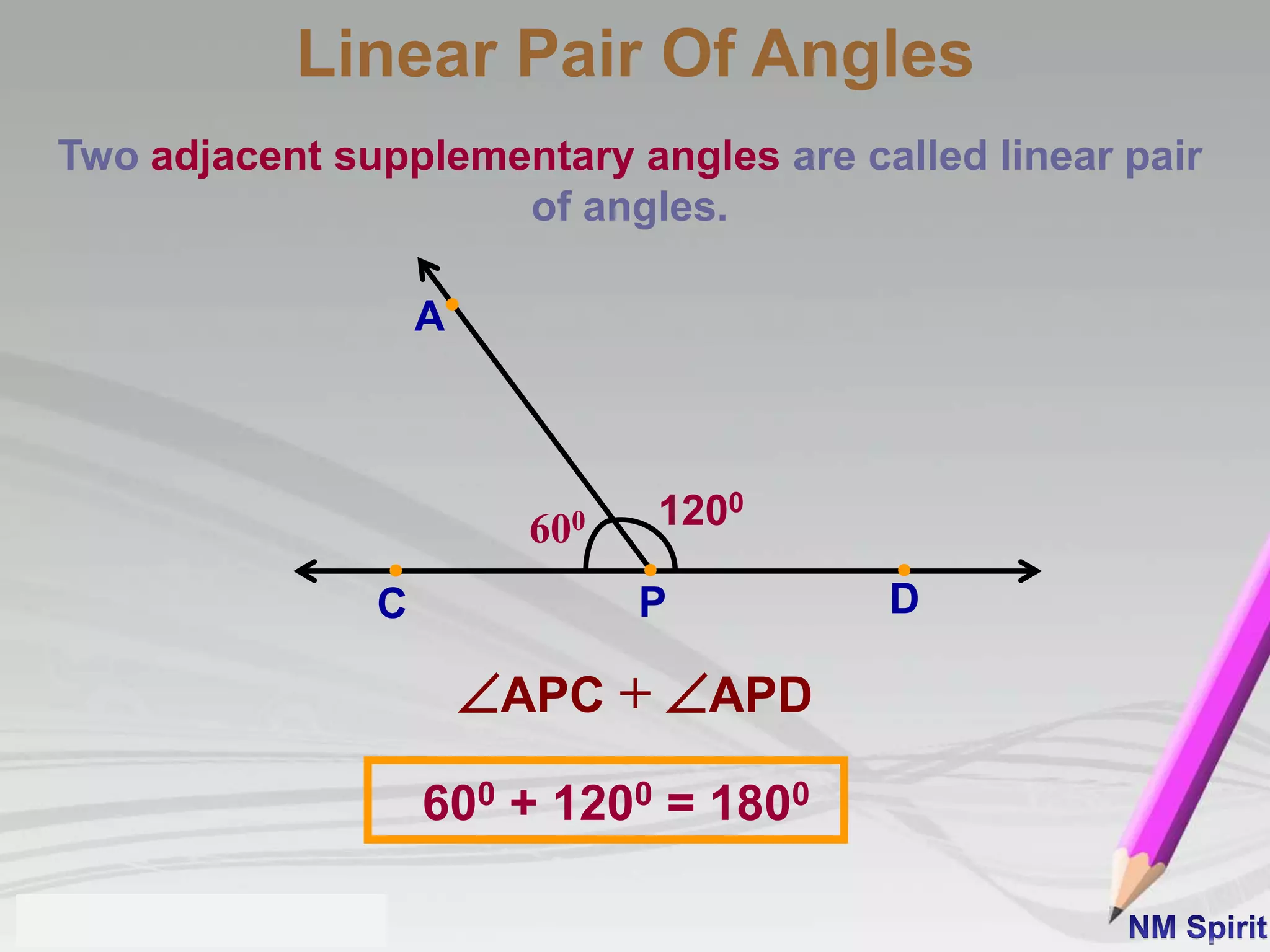
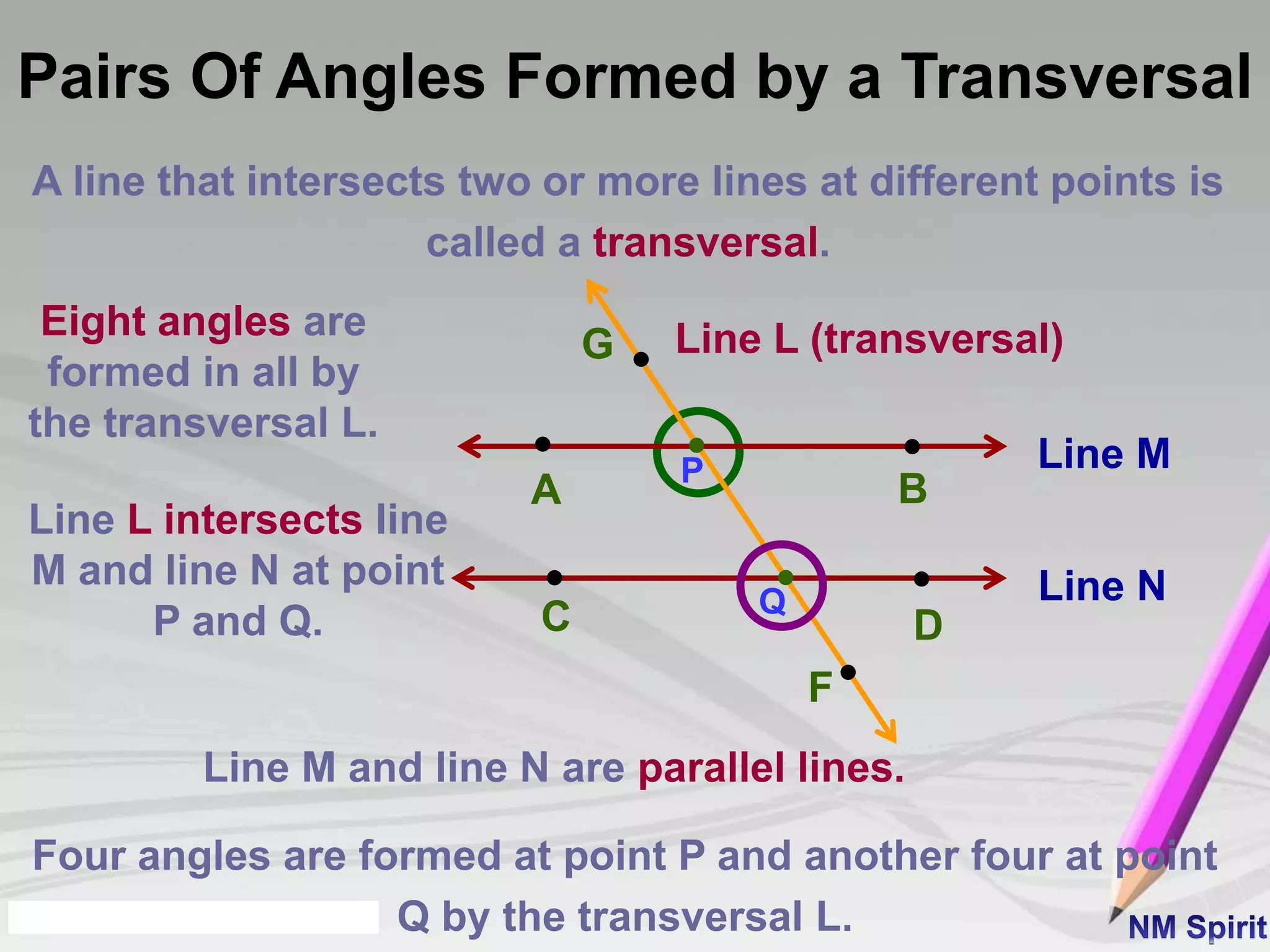
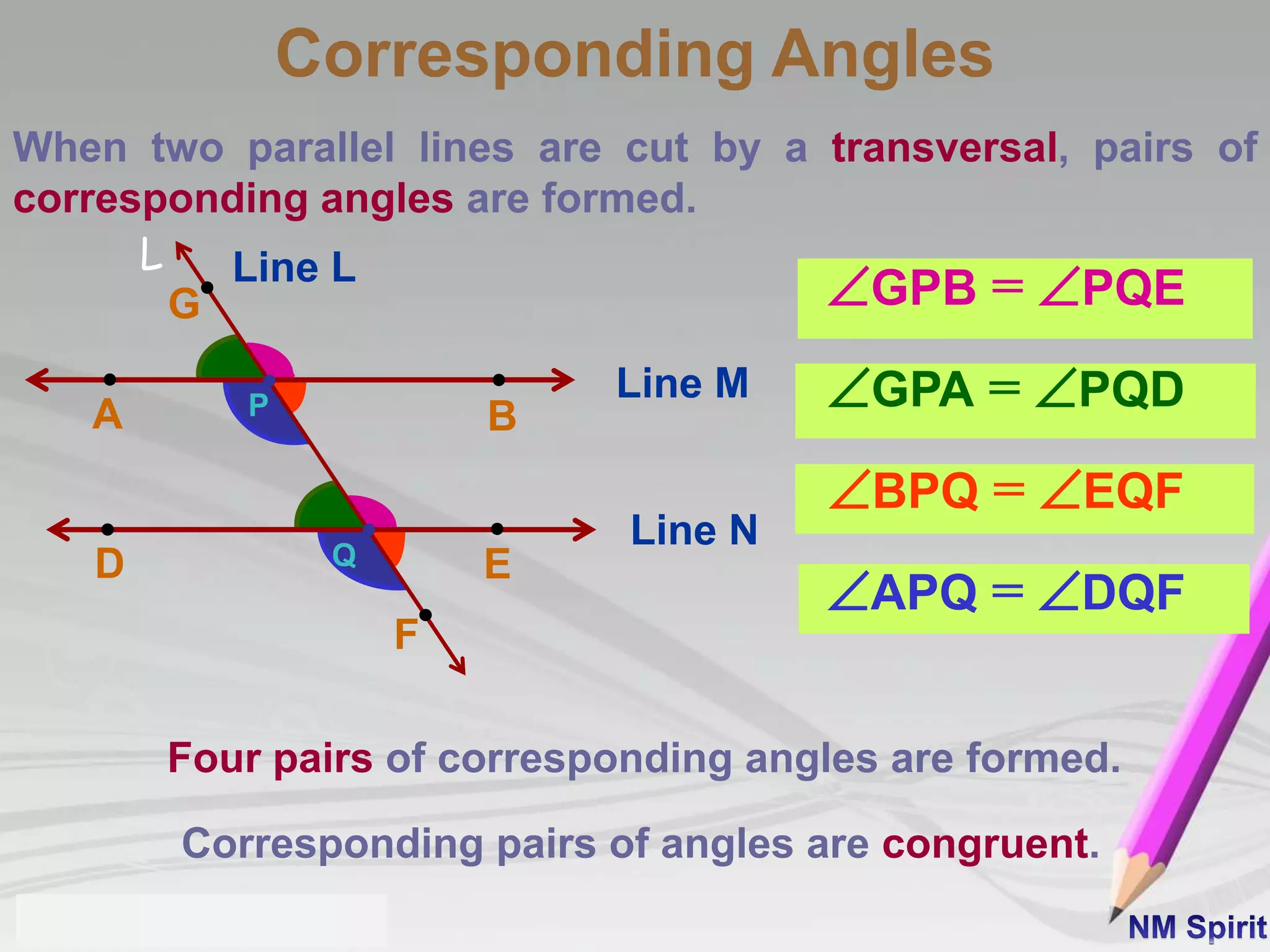
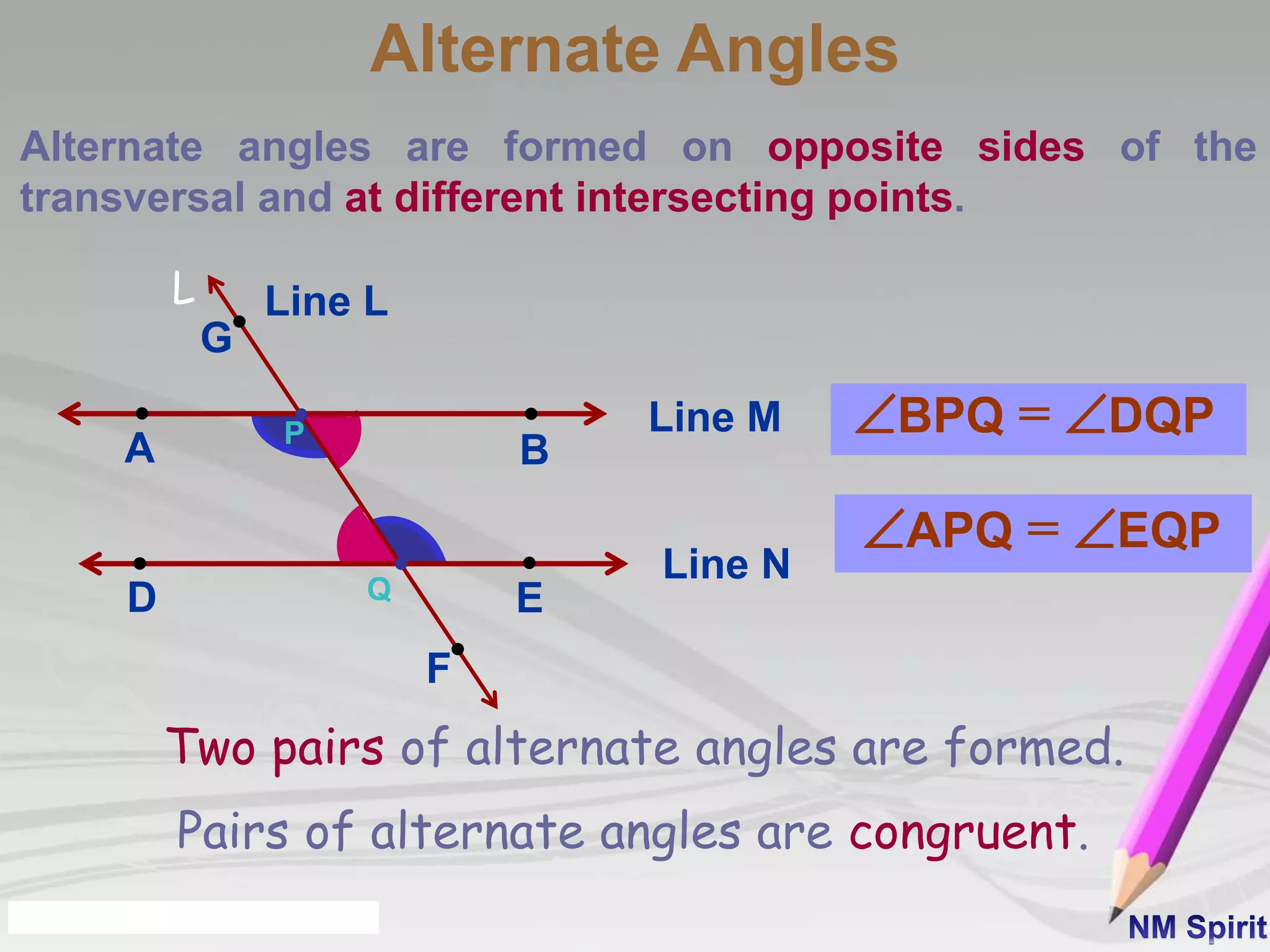
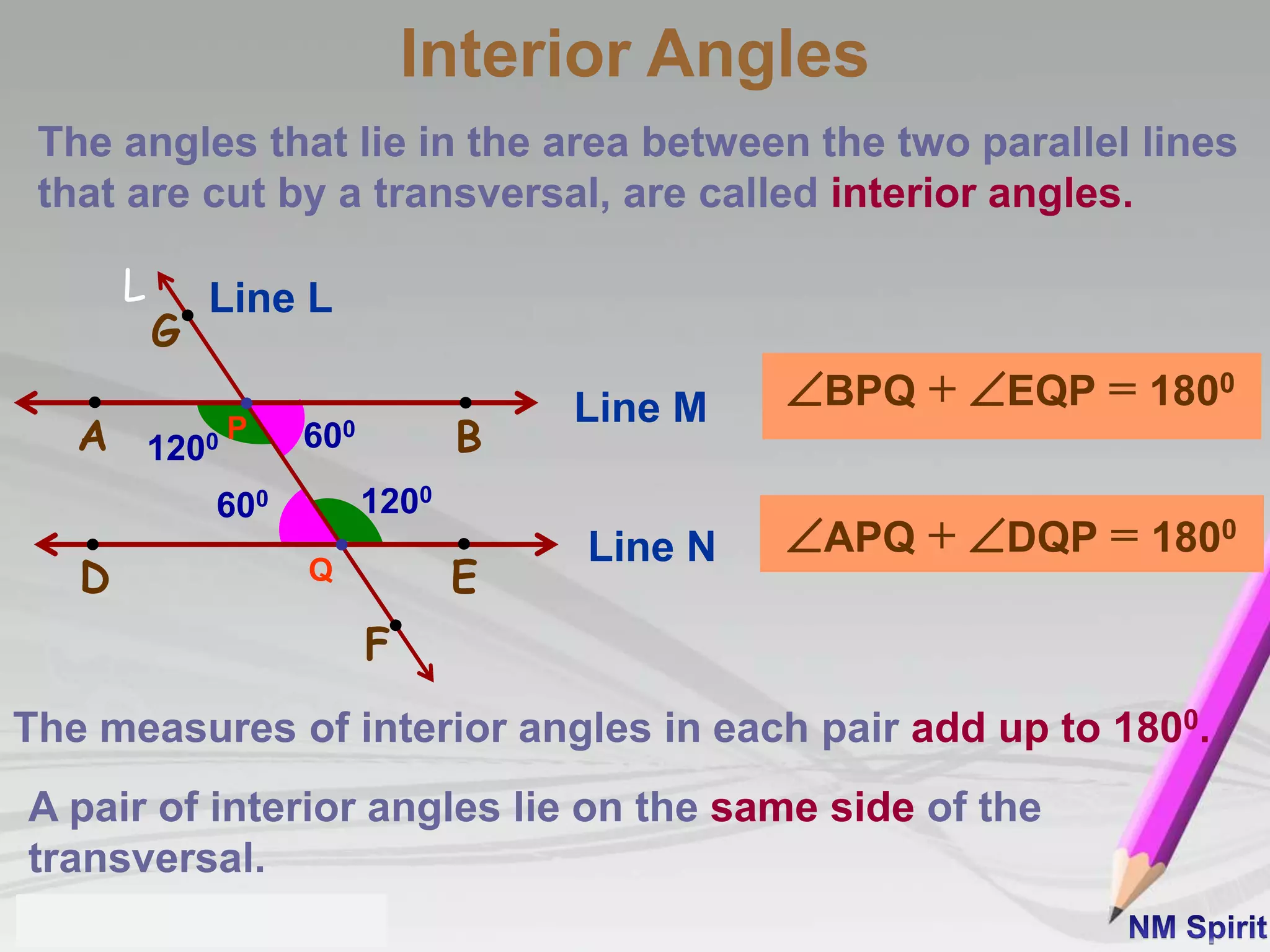
This document defines and describes different types of angles: 1) Adjacent angles share a common vertex and side. Vertically opposite angles are formed when two lines intersect and are equal. 2) Complementary angles have a sum of 90 degrees. Supplementary angles have a sum of 180 degrees. 3) A linear pair is two adjacent supplementary angles. 4) A transversal intersects two or more lines. It forms corresponding, alternate, and interior angles that follow specific properties.

1. Pairs of Angles :
Types• Adjacent angles
• Vertically opposite angles
• Complementary angles
• Supplementary angles
• Linear pairs of angles

2. Adjacent Angles
Two angles that have a common vertex and a common ray
are called adjacent angles.
C
D
B
A
Common ray
Common vertex
Adjacent Angles ABD and DBC
Adjacent angles do not overlap each other.
D
E
F
A
B
C
ABC and DEF are not adjacent angles

3. Vertically Opposite Angles
Vertically opposite angles are pairs of angles formed by two
lines intersecting at a point.
APC = BPD
APB = CPD
A
DB
C
P
Four angles are formed at the point of intersection.
Point of intersection ‘P’ is the common vertex of the four
angles.
Vertically opposite angles are congruent.

4. If the sum of two angles is 900, then they are called
complementary angles.
600
A
B
C
300
D
E
F
ABC and DEF are complementary because
600 + 300 = 900
ABC + DEF
Complementary Angles

5. If the sum of two angles is 1800 then they are called
supplementary angles.
PQR and ABC are supplementary, because
1000 + 800 = 1800
RQ
P
A
B
C
1000
800
PQR + ABC
Supplementary Angles

6. Two adjacent supplementary angles are called linear pair
of angles.
A
600 1200
PC D
600 + 1200 = 1800
APC + APD
Linear Pair Of Angles

7. A line that intersects two or more lines at different points is
called a transversal.
Line L (transversal)
BA
Line M
Line N
DC
P
Q
G
F
Pairs Of Angles Formed by a Transversal
Line M and line N are parallel lines.
Line L intersects line
M and line N at point
P and Q.
Four angles are formed at point P and another four at point
Q by the transversal L.
Eight angles are
formed in all by
the transversal L.

8. Pairs Of Angles Formed by a Transversal
• Corresponding angles
• Alternate angles
• Interior angles

9. Corresponding Angles
When two parallel lines are cut by a transversal, pairs of
corresponding angles are formed.
Four pairs of corresponding angles are formed.
Corresponding pairs of angles are congruent.
GPB = PQE
GPA = PQD
BPQ = EQF
APQ = DQF
Line M
BA
Line N
D E
L
P
Q
G
F
Line L

10. Alternate Angles
Alternate angles are formed on opposite sides of the
transversal and at different intersecting points.
Line M
BA
Line N
D E
L
P
Q
G
F
Line L
BPQ = DQP
APQ = EQP
Pairs of alternate angles are congruent.
Two pairs of alternate angles are formed.

11. The angles that lie in the area between the two parallel lines
that are cut by a transversal, are called interior angles.
A pair of interior angles lie on the same side of the
transversal.
The measures of interior angles in each pair add up to 1800.
Interior Angles
Line M
BA
Line N
D E
L
P
Q
G
F
Line L
600
1200
1200
600
BPQ + EQP = 1800
APQ + DQP = 1800