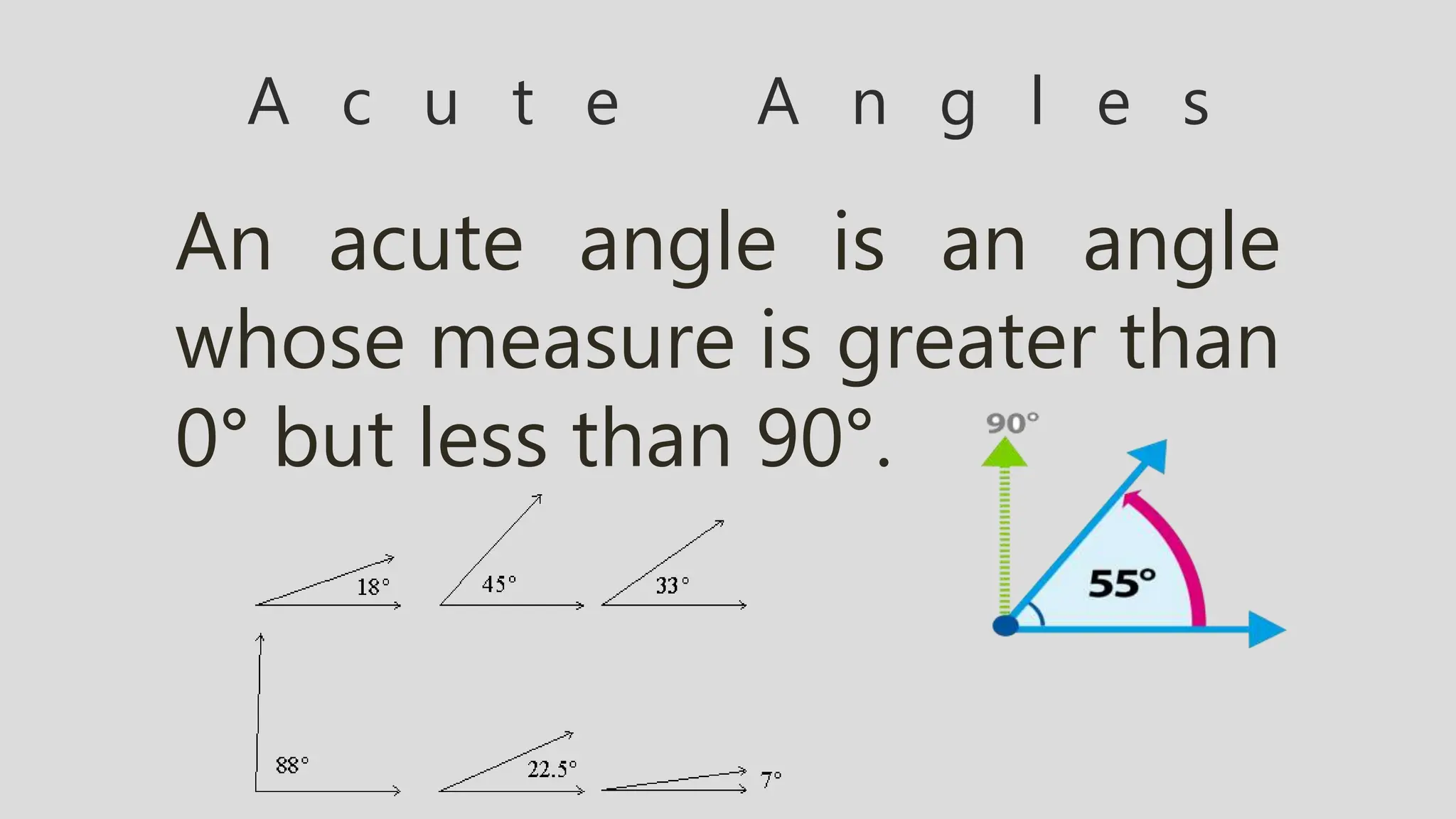
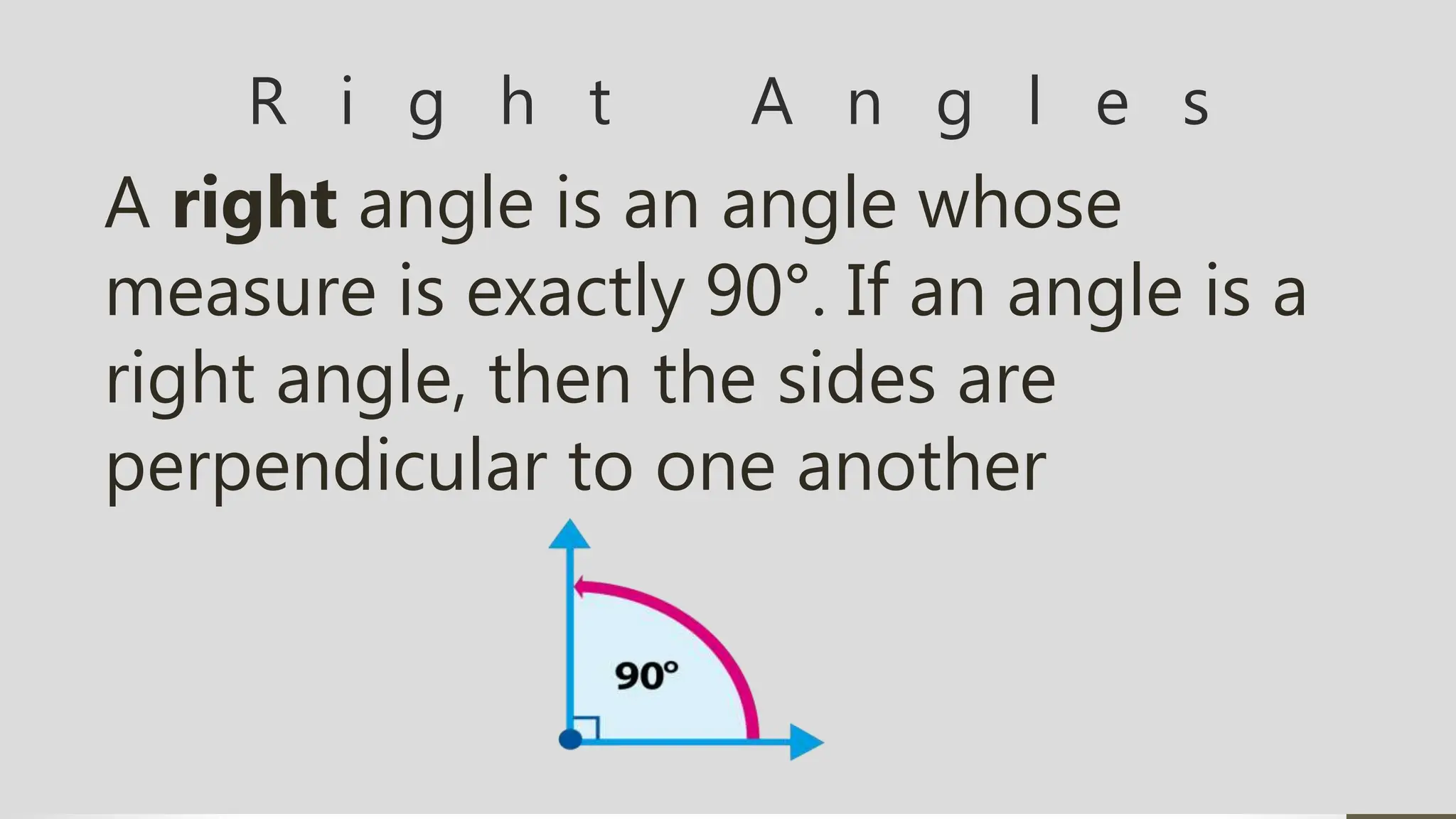
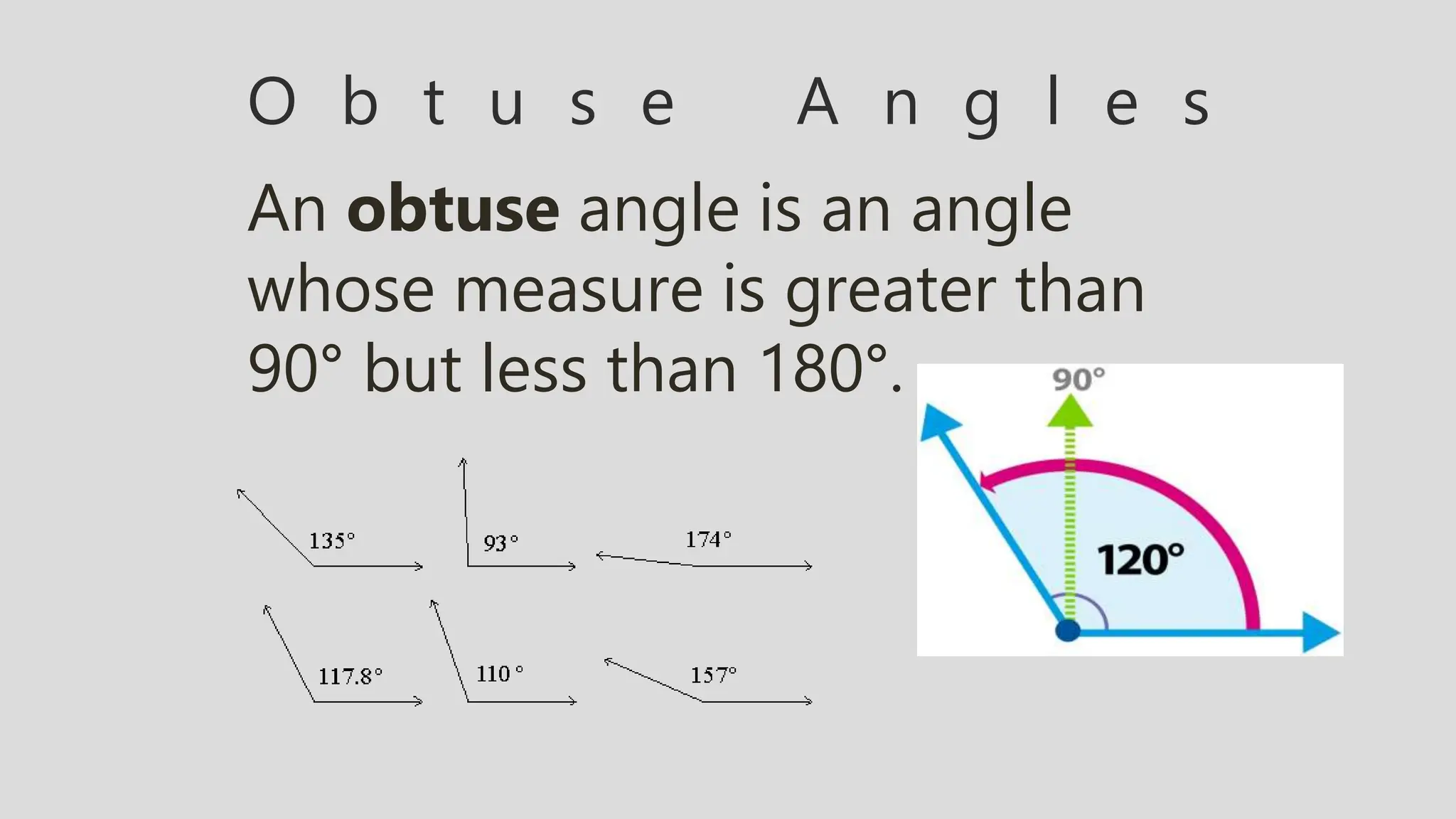
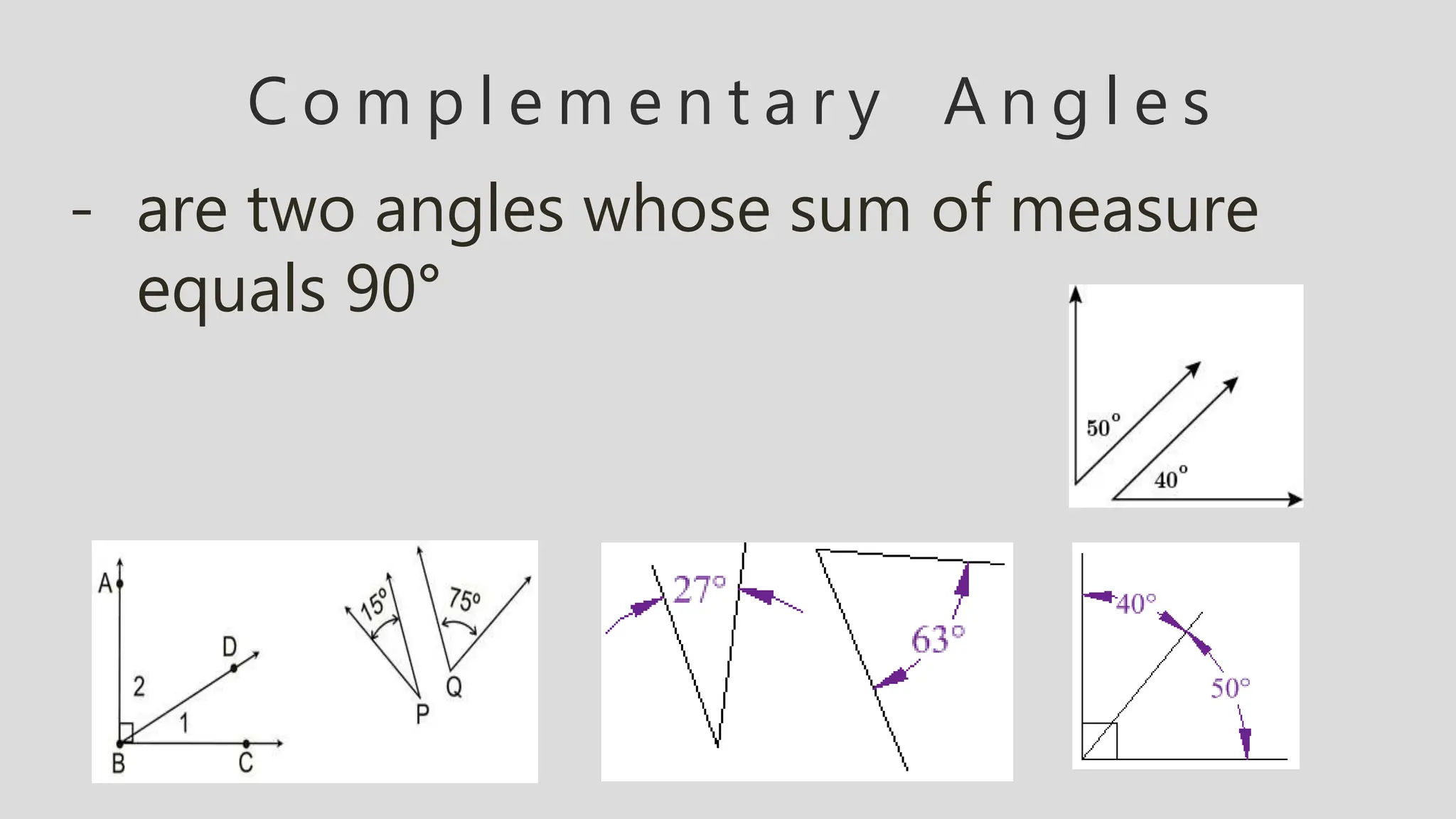
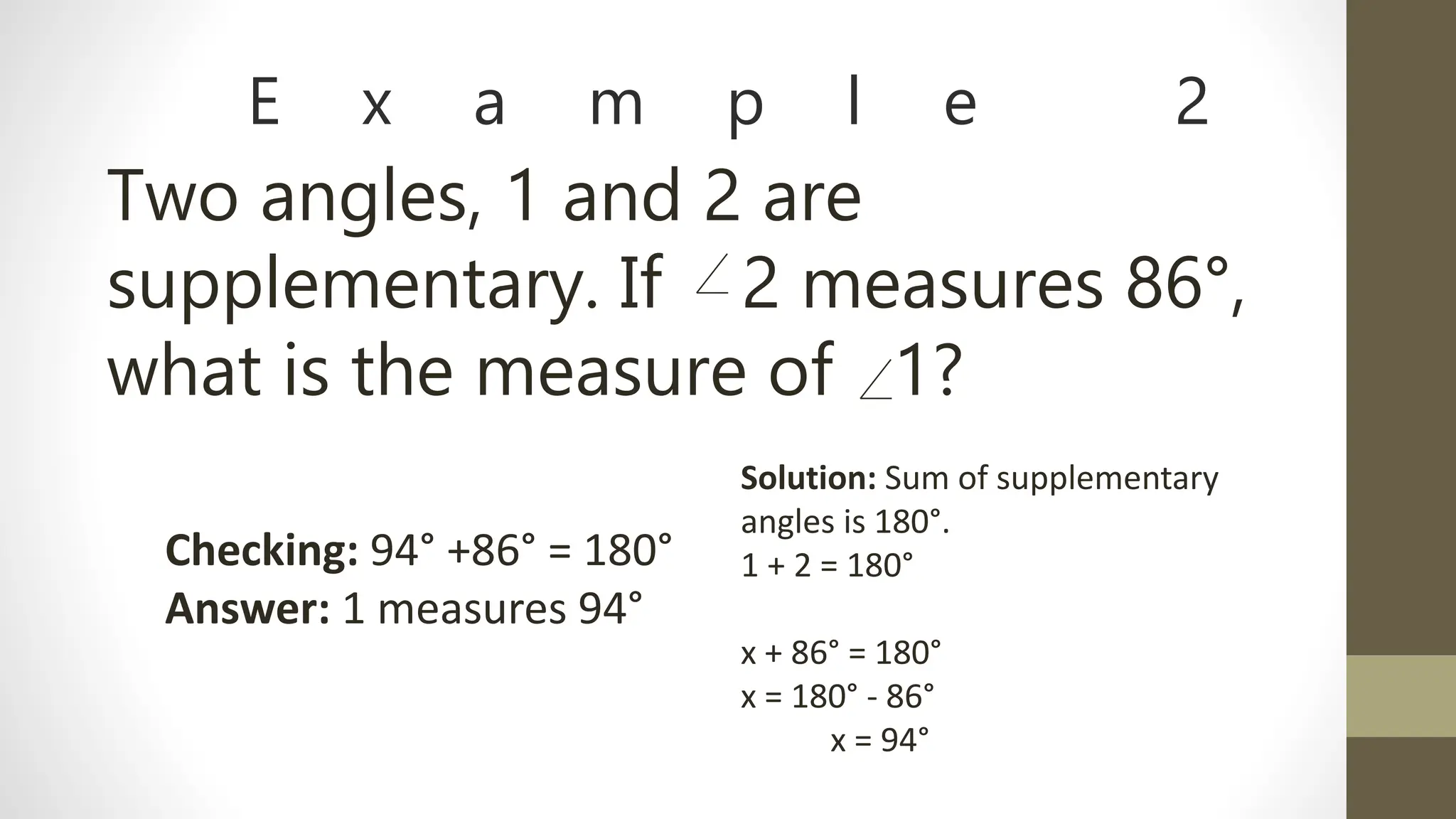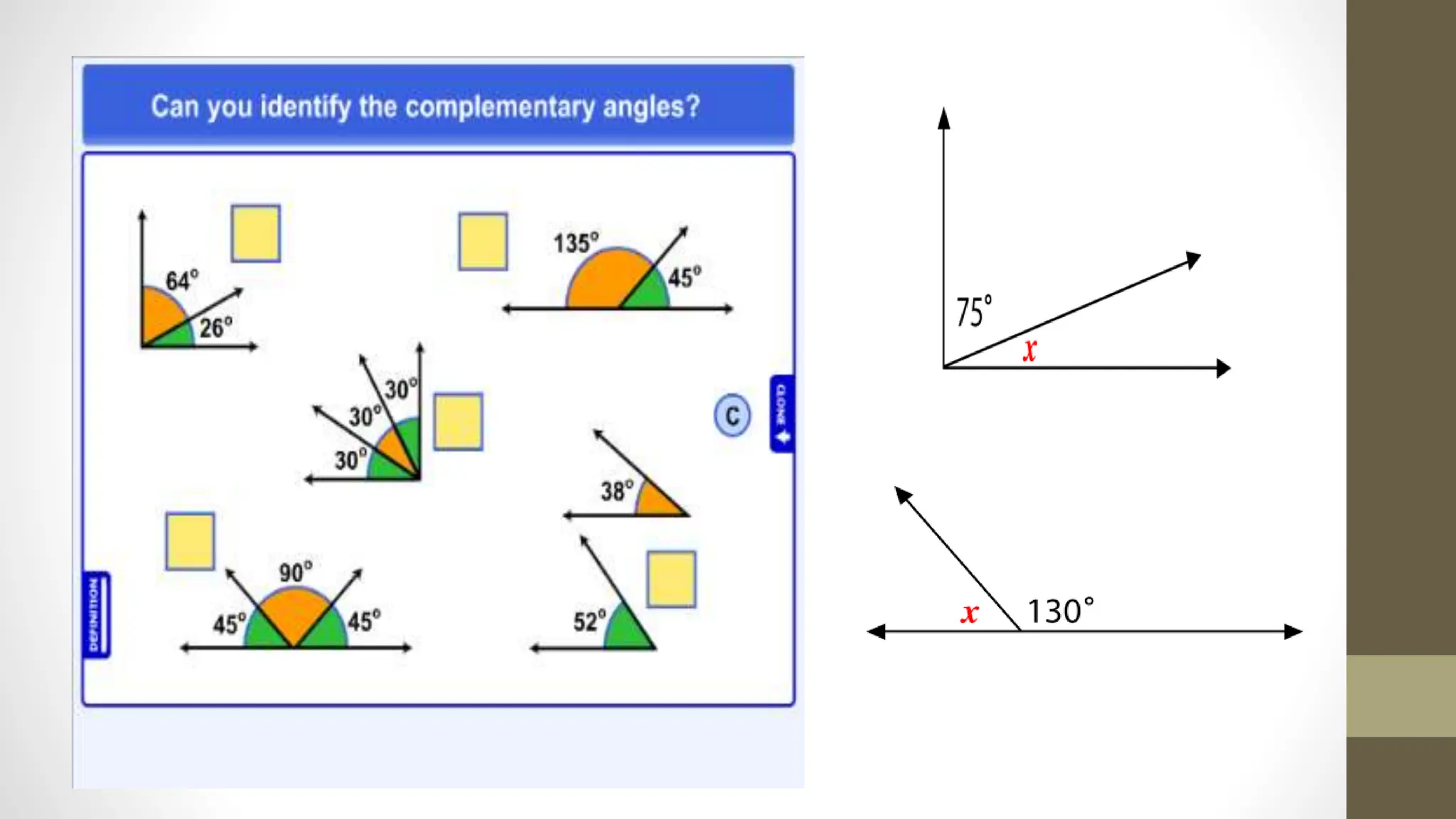
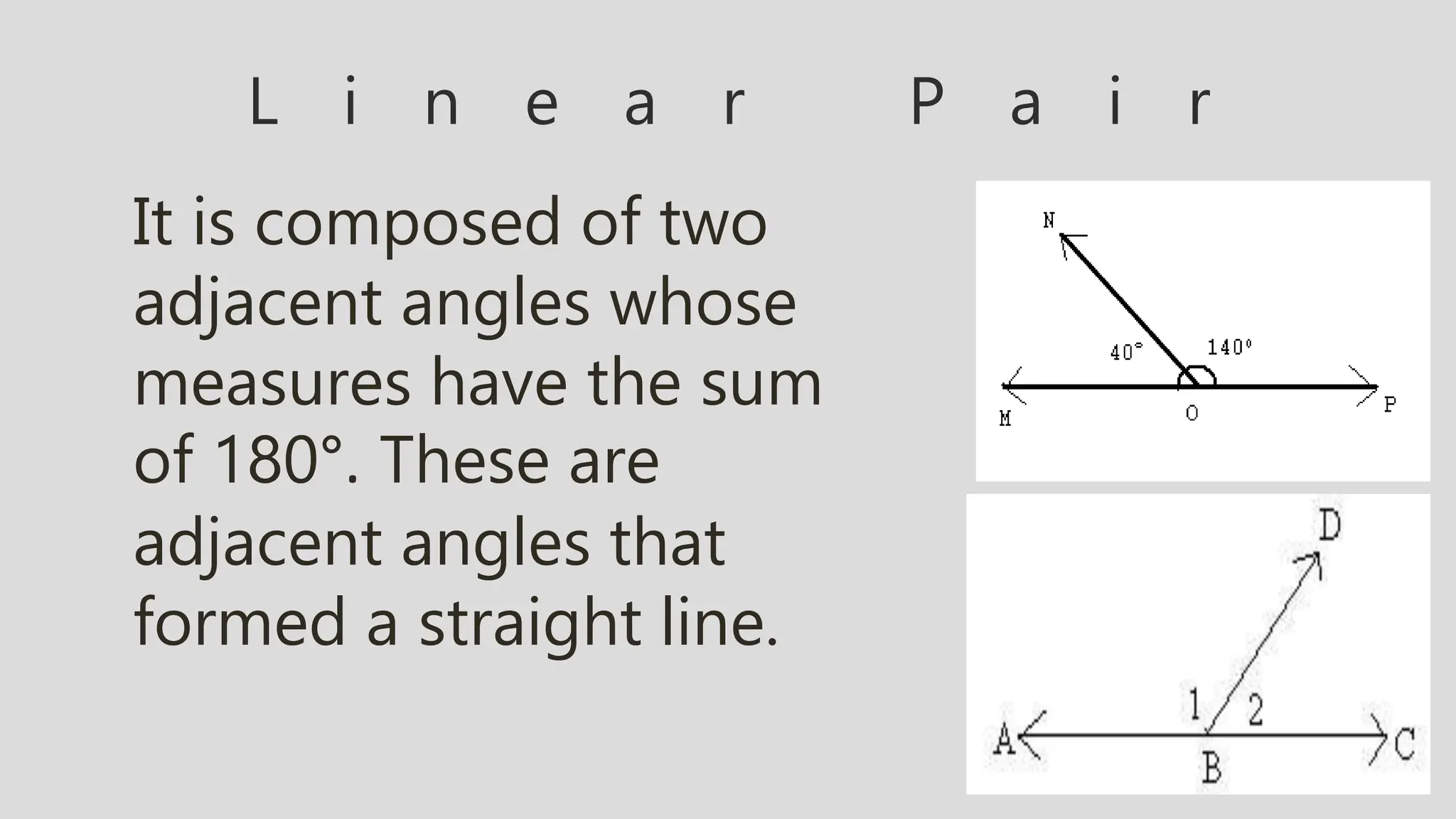
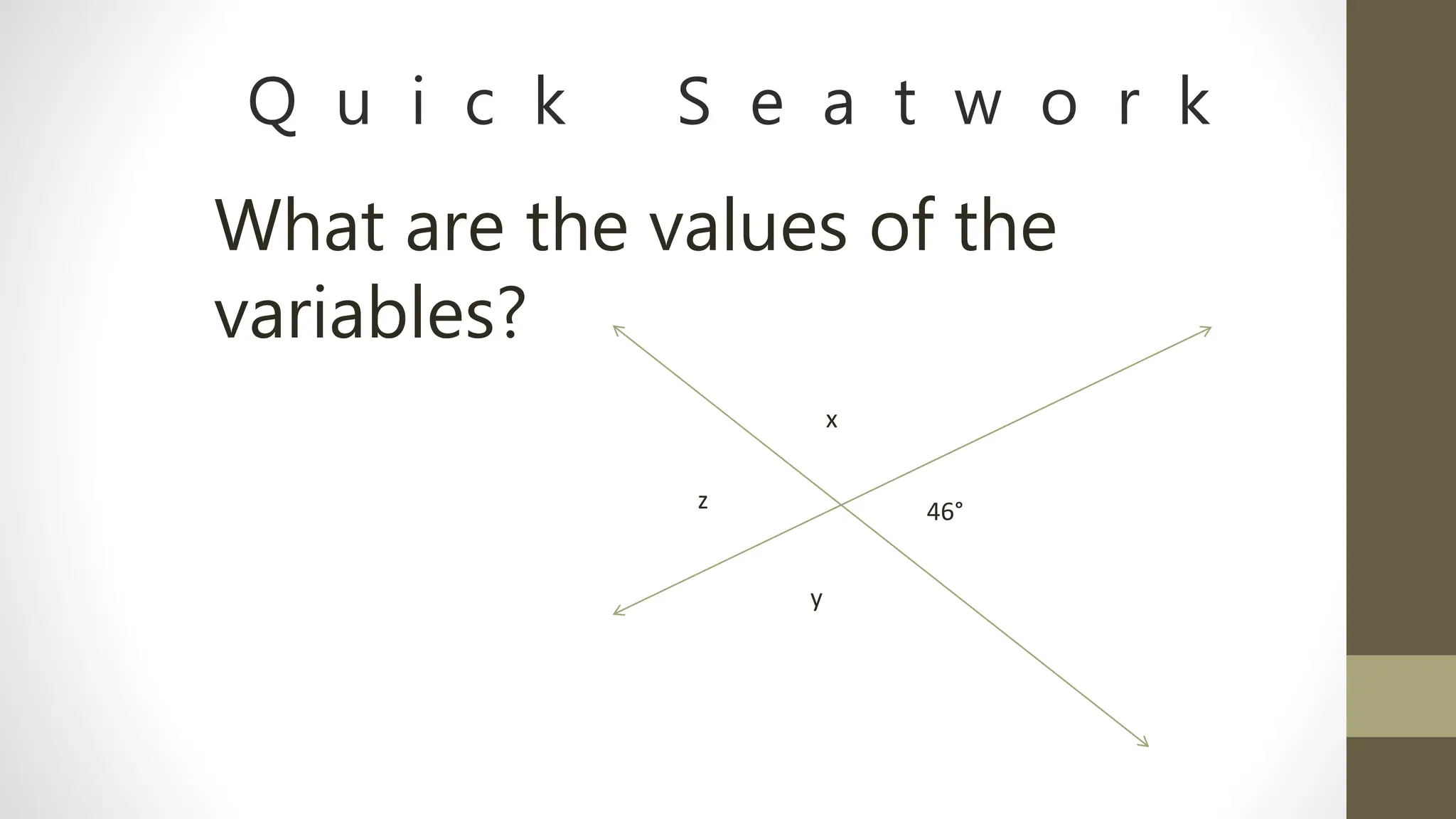
The document defines and describes different types of angles: - Acute angles are between 0 and 90 degrees. Right angles are exactly 90 degrees. Obtuse angles are between 90 and 180 degrees. - Angles are also defined based on their relationship to each other, such as complementary (sum to 90 degrees), supplementary (sum to 180 degrees), adjacent, vertical, and corresponding angles formed by parallel lines cut by a transversal. - Examples are provided to demonstrate calculating unknown angle measures using relationships like complementary and supplementary angles. Protractors are used to measure angles in degrees.

1. A N G L E S

2. A n g l e s
It is figured formed by two rays
with a common endpoint, and
which are not on the same line.
The two rays are the sides of the
angle and the common endpoint
is called the vertex.

3. A n g l e s
An angle is named using a number, vertex
or a vertex and points on each side.
• If three letters are used to name an
angle, the middle letter should be the
vertex.
• If one letter is used, it should be the
vertex.

4. A n g l e s
Angles are measured using a
protractor and the unit of
measurement is degrees (°).

5. A n g l e s
Types of Angles

6. ACUTE ANGLE
OBTUSE ANGLE
RIGHT ANGLE
STRAIGHT ANGLE

7. A c u t e A n g l e s
An acute angle is an angle
whose measure is greater than
0° but less than 90°.

8. R i g h t A n g l e s
A right angle is an angle whose
measure is exactly 90°. If an angle is a
right angle, then the sides are
perpendicular to one another

9. O b t u s e A n g l e s
An obtuse angle is an angle
whose measure is greater than
90° but less than 180°.

10. Relationships Between Angles
Adjacent angles are two distinct
angles with common vertex and a
common side.

11. Complementary Angles
Supplementary Angles

12. C o m p l e m e n t a r y A n g l e s
- are two angles whose sum of measure
equals 90°

13. S u p p l e m e n t a r y A n g l e s
- are two angles whose
measures have the sum of
180°

14. E x a m p l e 1
Two angles are adjacent if they have
common vertex and a common side.
In the figure, are adjacent angles
since their vertex is at point 0 and
their common side is ray.

16. E x a m p l e 2
What must be the measure of
K to complement J?
72°
J
K
Solution: Sum of
complementary angles
is 90°.
J = 72° ; K = x°
J + K = 90°
72° + x° = 90°
x = 90° - 72°
x = 18°
Checking: 72° + 18° = 90°
Answer: Angle K measures 18°

17. E x a m p l e 2
Two angles, 1 and 2 are
supplementary. If 2 measures 86°,
what is the measure of 1?
Solution: Sum of supplementary
angles is 180°.
1 + 2 = 180°
x + 86° = 180°
x = 180° - 86°
x = 94°
Checking: 94° +86° = 180°
Answer: 1 measures 94°

18. L i n e a r P a i r
It is composed of two
adjacent angles whose
measures have the sum
of 180°. These are
adjacent angles that
formed a straight line.

19. V e r t i c a l A n g l e s
- are two nonadjacent angles
formed by two intersecting
lines. Vertical angles are
congruent.

20. Q u i c k S e a t w o r k
What are the values of the
variables?
z
y
x
46°

21. Parallel Cut by a Transversal
Given 𝑙1is parallel to 𝑙2 and 𝑙3
is a transversal line.
𝑙2
𝑙1
𝑙3
e
f g
h
b
a
c
d

22. Parallel Cut by a Transversal
Given that the parallel lines are cut
by a transversal, the following
relationships are true:
1. Alternate interior angles are
congruent.
2. Alternate exterior angles are
congruent.