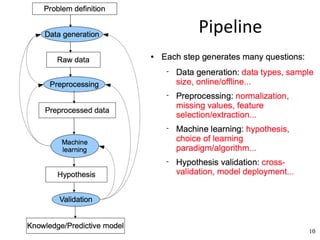
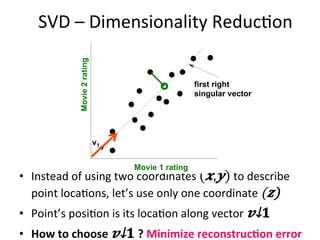
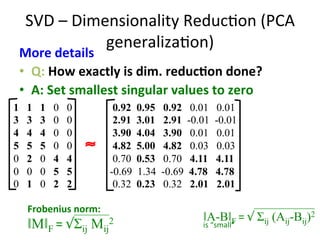
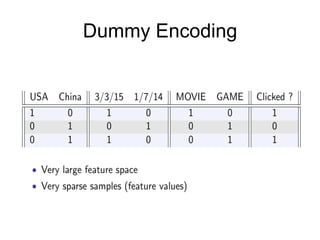
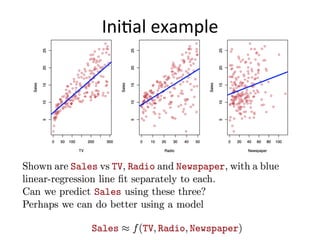
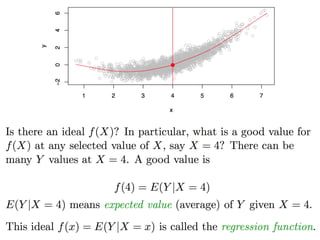
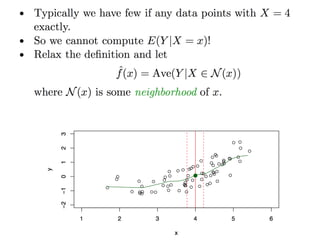
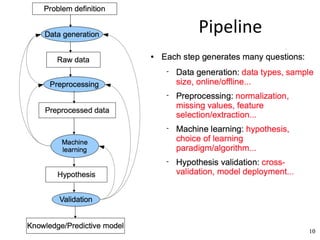
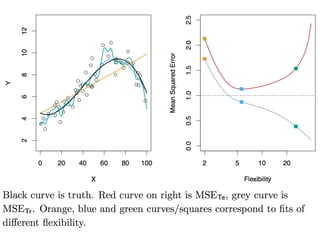
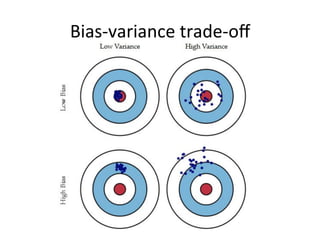
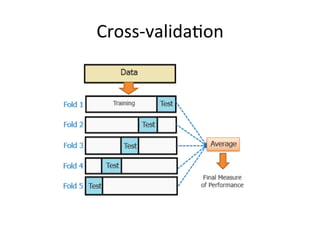
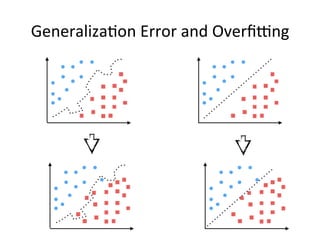
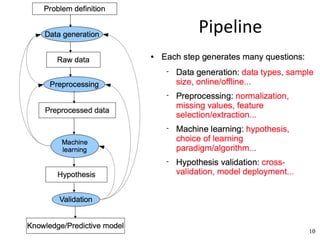
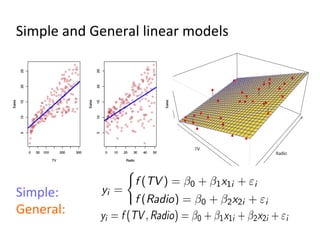
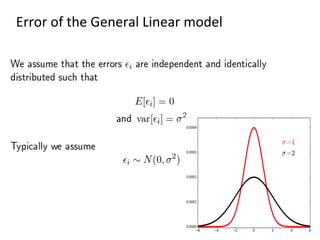
The document discusses supervised learning algorithms and their importance in the field of machine learning, highlighting key concepts like data collection methods, model evaluation, and dimensionality reduction. It covers generalized linear models for different types of data and addresses the challenges faced when selecting features due to high dimensionality. Additionally, it provides a summary of methodological insights and references for further reading.

1. Supervised
Learning
Algorithms
Analysis
of
Different
approaches
Evgeniy Marinov
ML Consultant
Philip Yankov
x8academy

2. ML DefiniCon
• There are plenty of definiCons...
• Informal: The field of study that gives
computers the ability to learn without being
explicitly programmed (Arthur Samuel, 1959)
• Formal: A computer program is said to learn
from experience E, with respect to some task
T, and some performance measure P, if its
performance on T as measured by P improves
with experience E (Tom Mitchell, 1998).

3. From Wikipedia
• Machine learning is:
– a subfield of computer science that evolved from
the study of paRern recogniCon and in AI in the
1980s (ML is a separate field flourishing from the
1990s, first benefited from staCsCcs and then
from the increasing availability of digiCzed
informaCon at that Cme).

4. Why ML?

5. Why ML?

6. Key factors enabling ML growth today
• Cloud Compu)ng
• Internet of Things
• Big Data (+ Unstructured Data)

7. Why Data is so important?

8. Why Data is so important?
• Google Photos
– Unlimited storage
• Google voice
– OK, Google

10. Nowadays
• It is so easy to get data you need and to use
an API or service of some company to
experiment with them

11. Methods for collecCng data

12. Methods for collecCng data
• Download
– Spreadsheet
– Text
• API
• Crawling / scraping

13. Supervised Learning

14. Task Description

15. Pipeline

16. IniCal example

17. NotaCon

19. • Asdasd
• Asdasd
• Asdasd
• Asdasd
The regression funcCon f(x)

20. • as
• as
• as

21. How to evaluate our model?

22. Pipeline

23. Assessing the Model Accuracy

25. Bias-variance trade-off

26. Bias-variance trade-off

27. Cross-validaCon

28. GeneralizaCon Error and Overfi`ng

29. Choosing a Model by data types of
response

30. Pipeline

31. Data types and Generalized Linear
model
• Simple and General linear models
• RestricCons of the linear model
• Data type of the response Y
1) (General) Linear model R, Y ~ Gaussian(µ, σ^2) -- conCnuous
2) LogisCc regression {0, 1}, Y ~ Bernoulli(p) -- binary data
3) Poisson regression {0, 1,...}, Y ~ Poisson(µ) -- counCng data

32. Simple and General linear models
Simple:
General:

33. Error of the General Linear model
Click to add Text

34. RestricCons of Linear models
Although the General linear model is a useful
framework, it is not appropriate in the following cases:
• The range of Y is restricted (e.g. binary, count,
posiCve/negaCve)
• Var[Y] depends on the mean E[Y] (for the Gaussian
they are independent)
Name Mean Variance
Bernoulli(p) p p(1 - p)
Binomial(p, n) np np(1 - p)
Poisson(p) p p

35. Binary response Y – {0, 1}
• The Bernoulli(p) is discrete r.v. with two possible outcomes:
• p and q = 1 – p
• The parameter p does not change over Cme
• Bernoulli is building block for other more complicated
distribuCons
• Examples:
• Coin flips {Heads, Tails} – if unbiased
• then p = 0.5
• Click on Ad, Fail/Success on Exam

36. Generalized Linear model - IntuiCon

37. ExponenCal Family

38. General linear model

39. Binary Data

40. Modeling CounCng / Poisson Data

41. Maximizing the Log-Likelihood and Parameters
esCmaCon

42. Preprocessing

43. Pipeline

44. Problems with feature types
• Big number of features -> Dimensionality
reducCon -> SVD, PCA
– Dimensionality reduc)on: “compress” the data
from a high-dimensional representaCon into a
lower-dimensional one (useful for visualizaCon or
as an internal transformaCon for other ML
algorithms)
• Sparse features -> Hashing

45. • Instead of using two coordinates ( 𝒙, 𝒚) to describe
point locaCons, let’s use only one coordinate (𝒛)
• Point’s posiCon is its locaCon along vector ​ 𝒗↓ 𝟏
• How to choose ​ 𝒗↓ 𝟏 ? Minimize reconstruc)on error
SVD – Dimensionality ReducCon
v1
first right
singular vector
Movie 1 rating
Movie2rating

46. SVD - Dimensionality ReducCon
More details
• Q: How exactly is dim. reduc)on done?
• A: Set smallest singular values to zero
46
0.56 0.59 0.56 0.09 0.09
0.12 -0.02 0.12 -0.69 -0.69
0.40 -0.80 0.40 0.09 0.09
x x
1 1 1 0 0
3 3 3 0 0
4 4 4 0 0
5 5 5 0 0
0 2 0 4 4
0 0 0 5 5
0 1 0 2 2
0.13 0.02 -0.01
0.41 0.07 -0.03
0.55 0.09 -0.04
0.68 0.11 -0.05
0.15 -0.59 0.65
0.07 -0.73 -0.67
0.07 -0.29 0.32
12.4 0 0
0 9.5 0
0 0 1.3
≈

47. SVD - Dimensionality ReducCon
More details
• Q: How exactly is dim. reduc)on done?
• A: Set smallest singular values to zero
47
x x
1 1 1 0 0
3 3 3 0 0
4 4 4 0 0
5 5 5 0 0
0 2 0 4 4
0 0 0 5 5
0 1 0 2 2
0.13 0.02 -0.01
0.41 0.07 -0.03
0.55 0.09 -0.04
0.68 0.11 -0.05
0.15 -0.59 0.65
0.07 -0.73 -0.67
0.07 -0.29 0.32
12.4 0 0
0 9.5 0
0 0 1.3
0.56 0.59 0.56 0.09 0.09
0.12 -0.02 0.12 -0.69 -0.69
0.40 -0.80 0.40 0.09 0.09
≈

48. SVD - Dimensionality ReducCon
More details
• Q: How exactly is dim. reduc)on done?
• A: Set smallest singular values to zero
≈ x x
1 1 1 0 0
3 3 3 0 0
4 4 4 0 0
5 5 5 0 0
0 2 0 4 4
0 0 0 5 5
0 1 0 2 2
0.13 0.02
0.41 0.07
0.55 0.09
0.68 0.11
0.15 -0.59
0.07 -0.73
0.07 -0.29
12.4 0
0 9.5
0.56 0.59 0.56 0.09 0.09
0.12 -0.02 0.12 -0.69 -0.69

49. ǁA-BǁF = √ Σij (Aij-Bij)2
is “small”
SVD – Dimensionality ReducCon (PCA
generalizaCon)
More details
• Q: How exactly is dim. reduc)on done?
• A: Set smallest singular values to zero
≈
1 1 1 0 0
3 3 3 0 0
4 4 4 0 0
5 5 5 0 0
0 2 0 4 4
0 0 0 5 5
0 1 0 2 2
0.92 0.95 0.92 0.01 0.01
2.91 3.01 2.91 -0.01 -0.01
3.90 4.04 3.90 0.01 0.01
4.82 5.00 4.82 0.03 0.03
0.70 0.53 0.70 4.11 4.11
-0.69 1.34 -0.69 4.78 4.78
0.32 0.23 0.32 2.01 2.01
Frobenius norm:
ǁMǁF = √Σij Mij
2

50. Feature selection - example

51. Dummy Encoding

52. (De)MoCvaCon

53. SoluCon to those problems with
features

54. Pipeline

55. Factorization Machine (degree 2)

56. General Applications of FMs

57. Summary Pipeline

58. Pipeline

59. From prototype to producCon
• Prototype vs ProducCon Cme? – model
(pipeline) should stay the same

60. Libraries

61. QuesCons?

62. Thank you!!!

63. References
• hRps://www.coursera.org/learn/machine-
learning
• hRp://www.cs.cmu.edu/~tom/
• hRp://scikit-learn.org/stable/
• hRp://www.scalanlp.org/
• hRp://www.algo.uni-konstanz.de/members/
rendle/pdf/Rendle2010FM.pdf
• hRps://securityintelligence.com/factorizaCon-
machines-a-new-way-of-looking-at-machine-
learning/

64. References
• An IntroducCon to Generalized Linear Models
– AnneRe Dobson, Adrian BarneR
• Applying Generalized Linear Models – James
Lindsey
• hRps://www.codementor.io/jadianes/
building-a-recommender-with-apache-spark-
python-example-app-part1-du1083qbw
• hRps://www.chrisstucchio.com/blog/
index.html