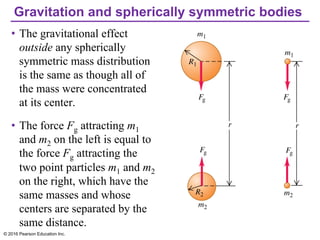
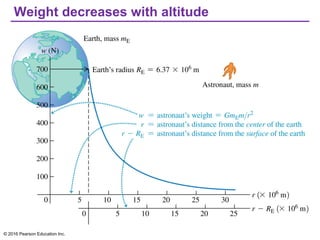
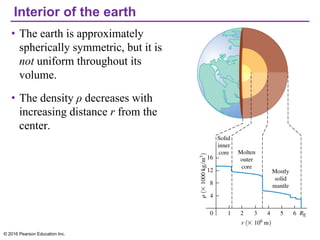
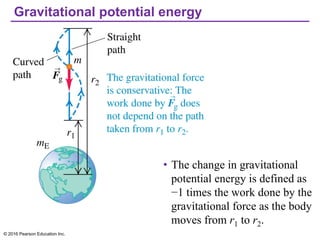
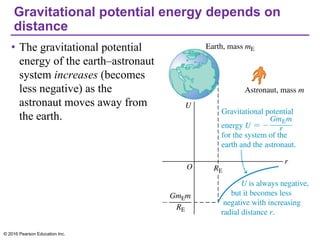
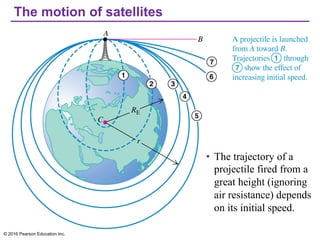
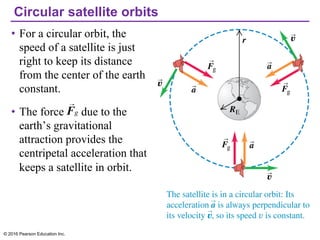
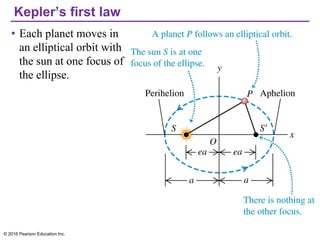
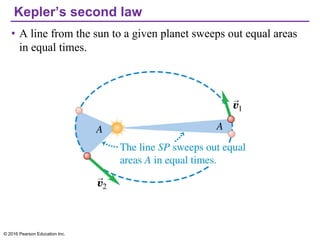
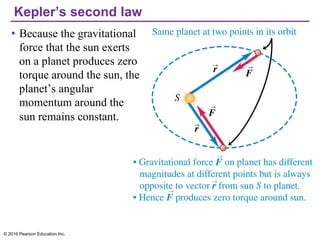
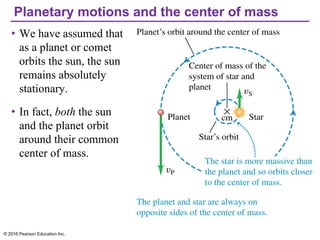
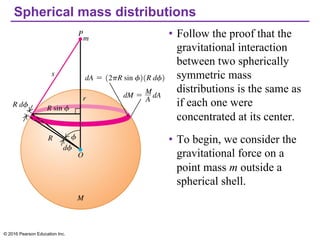
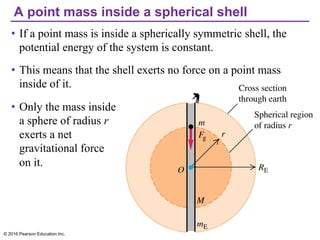
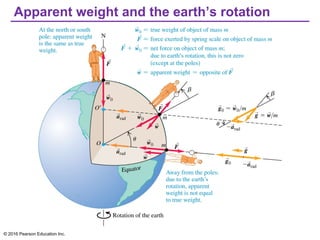
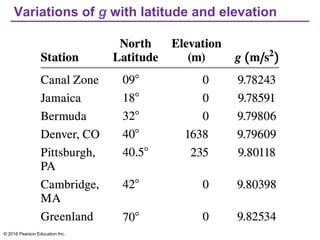
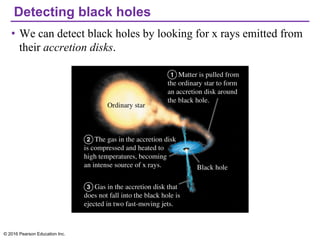
Chapter 13 discusses gravitation, focusing on how to calculate gravitational forces, weights, and the motion of satellites. It covers Newton's law of gravitation, Kepler's laws of planetary motion, and the nature of black holes, detailing their characteristics and detection methods. The chapter also addresses the effects of gravitational force in various contexts, including the behavior of objects on different celestial bodies.