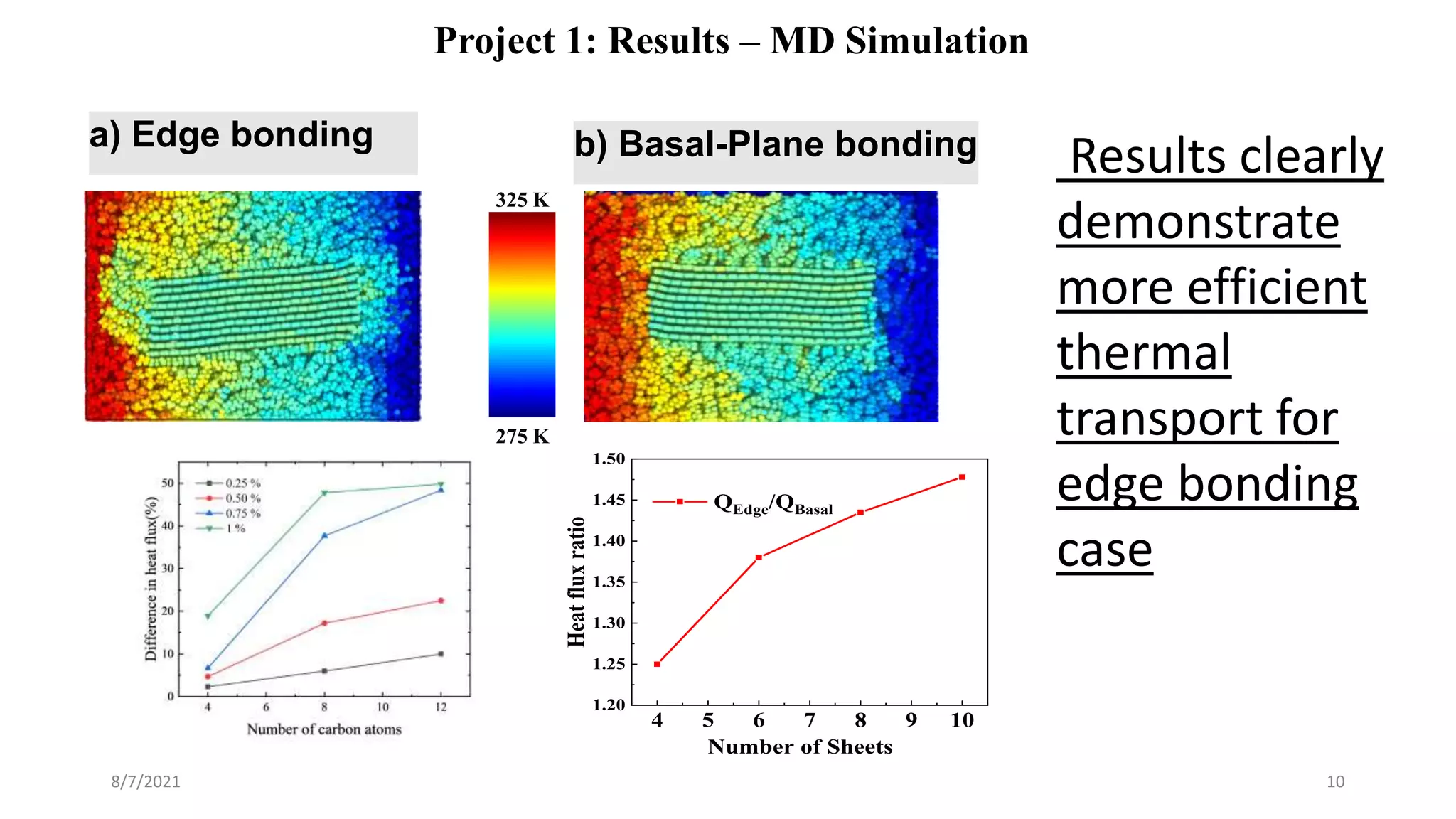
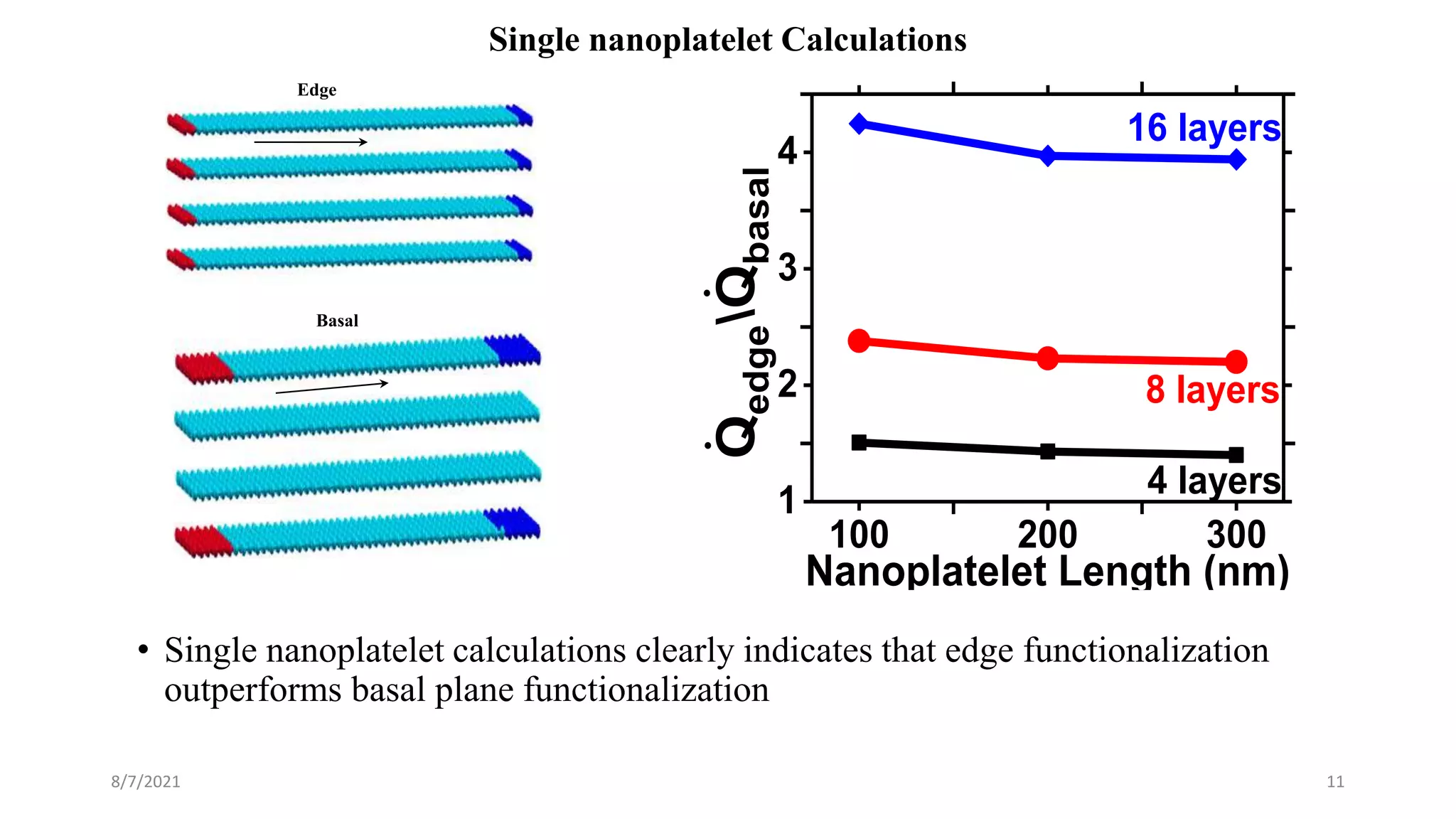
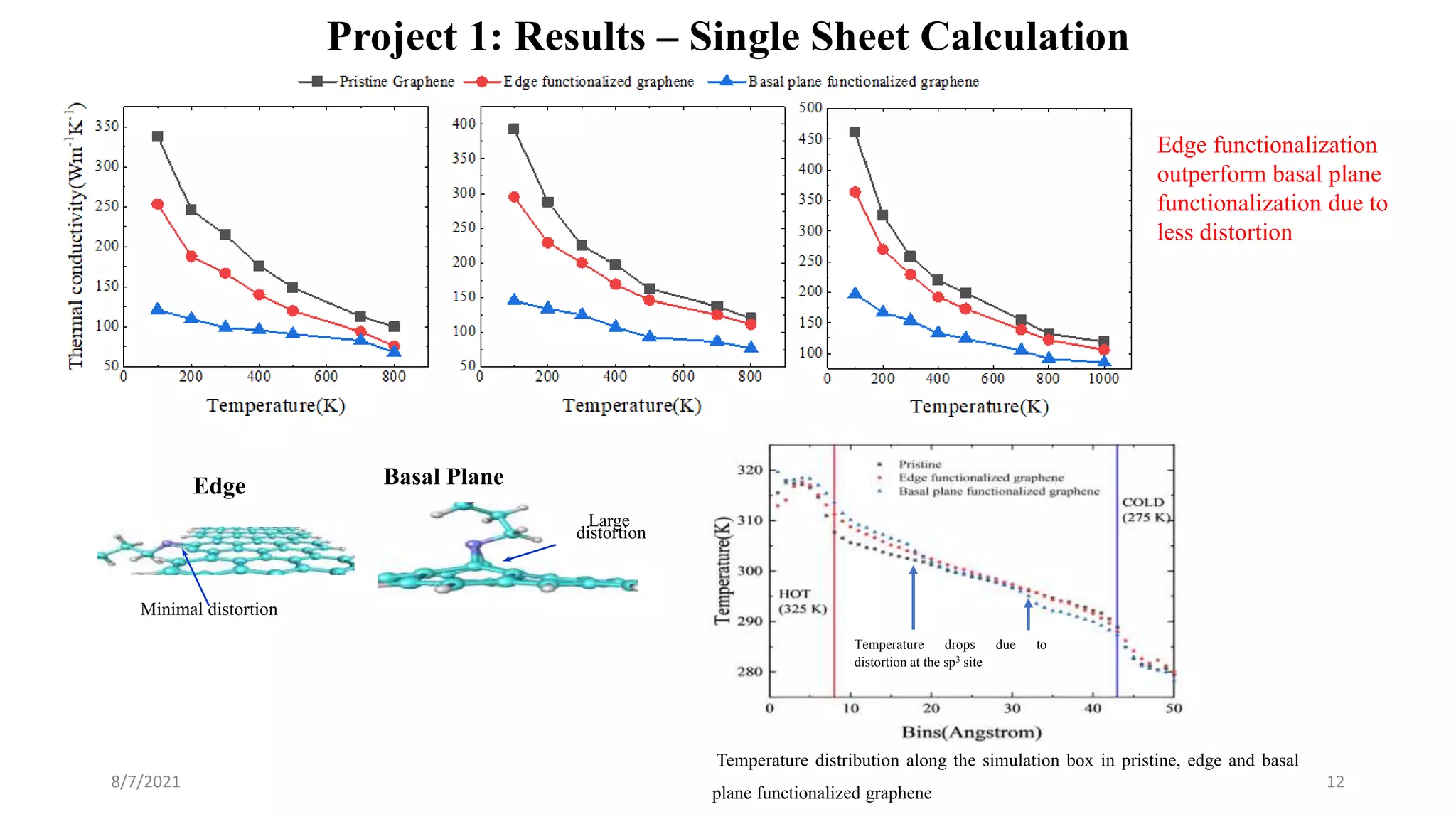
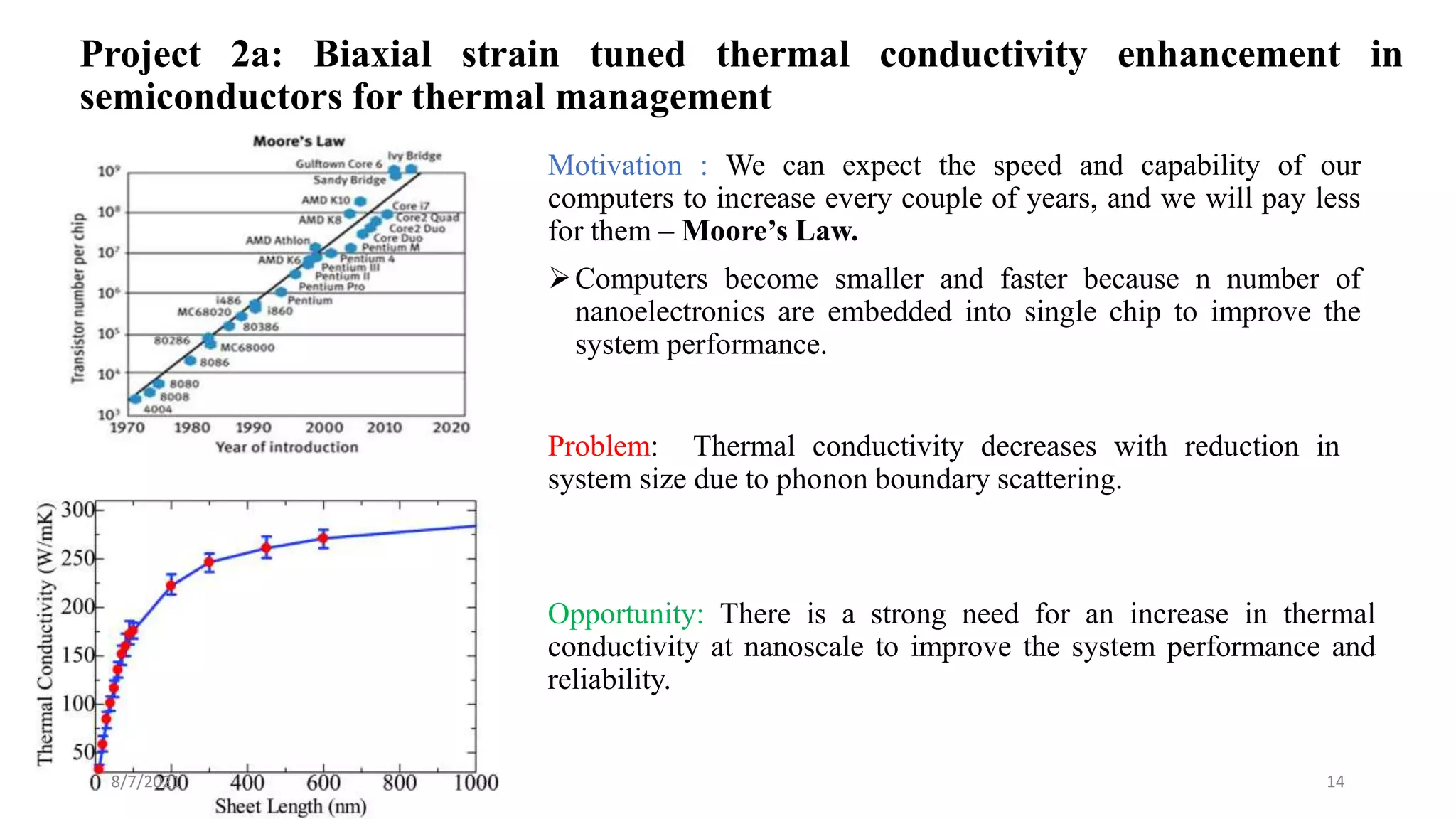
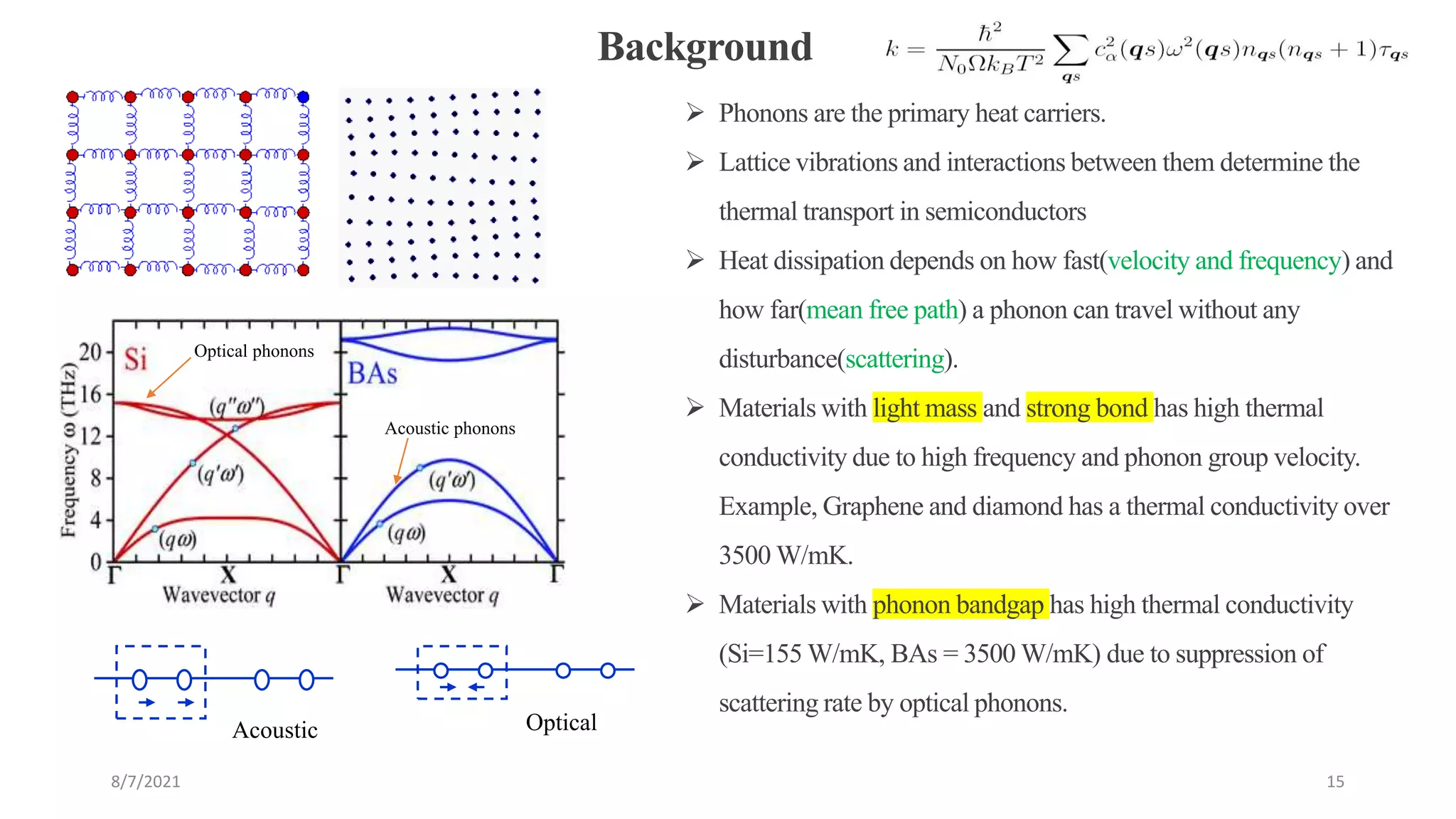
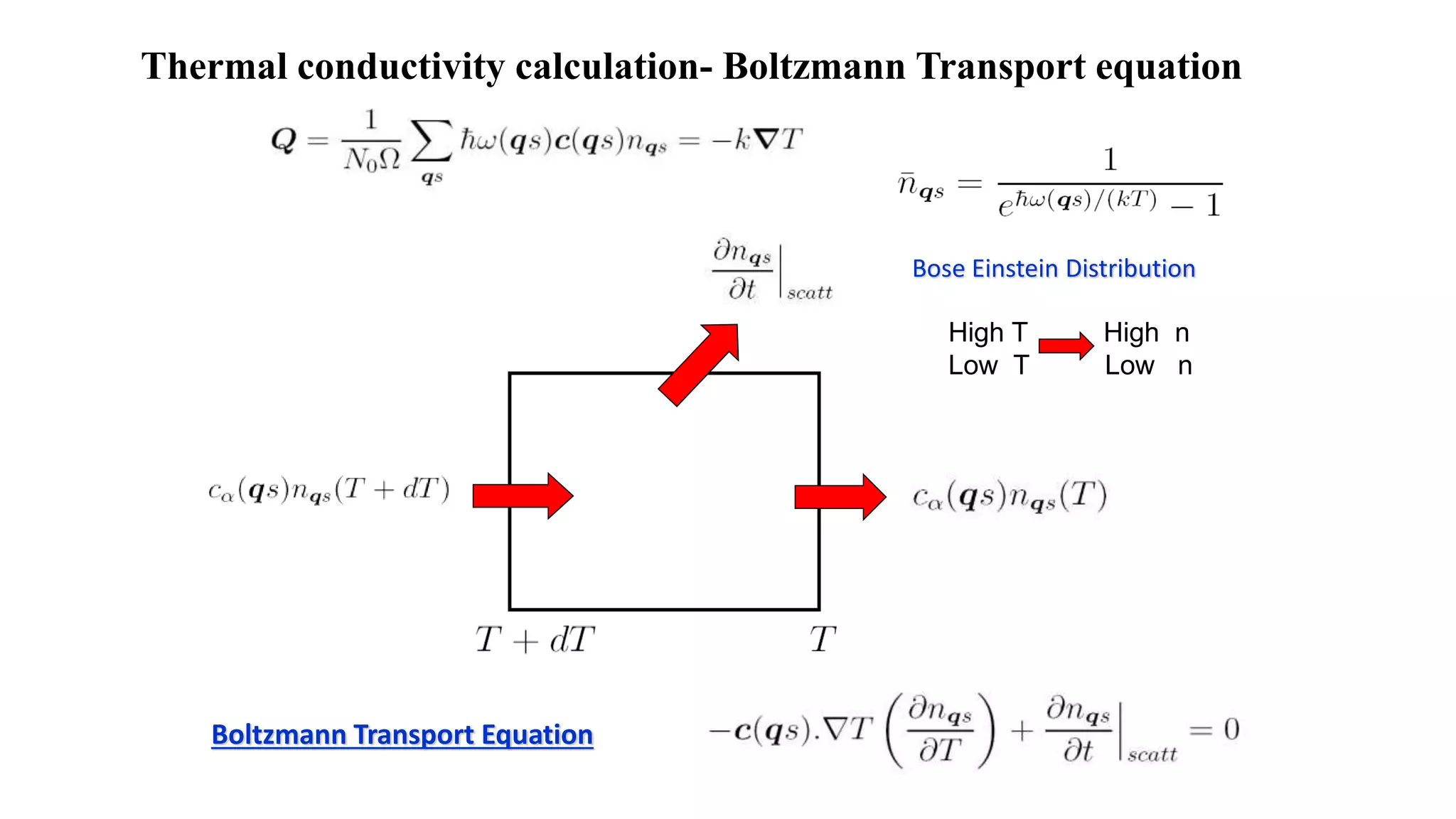
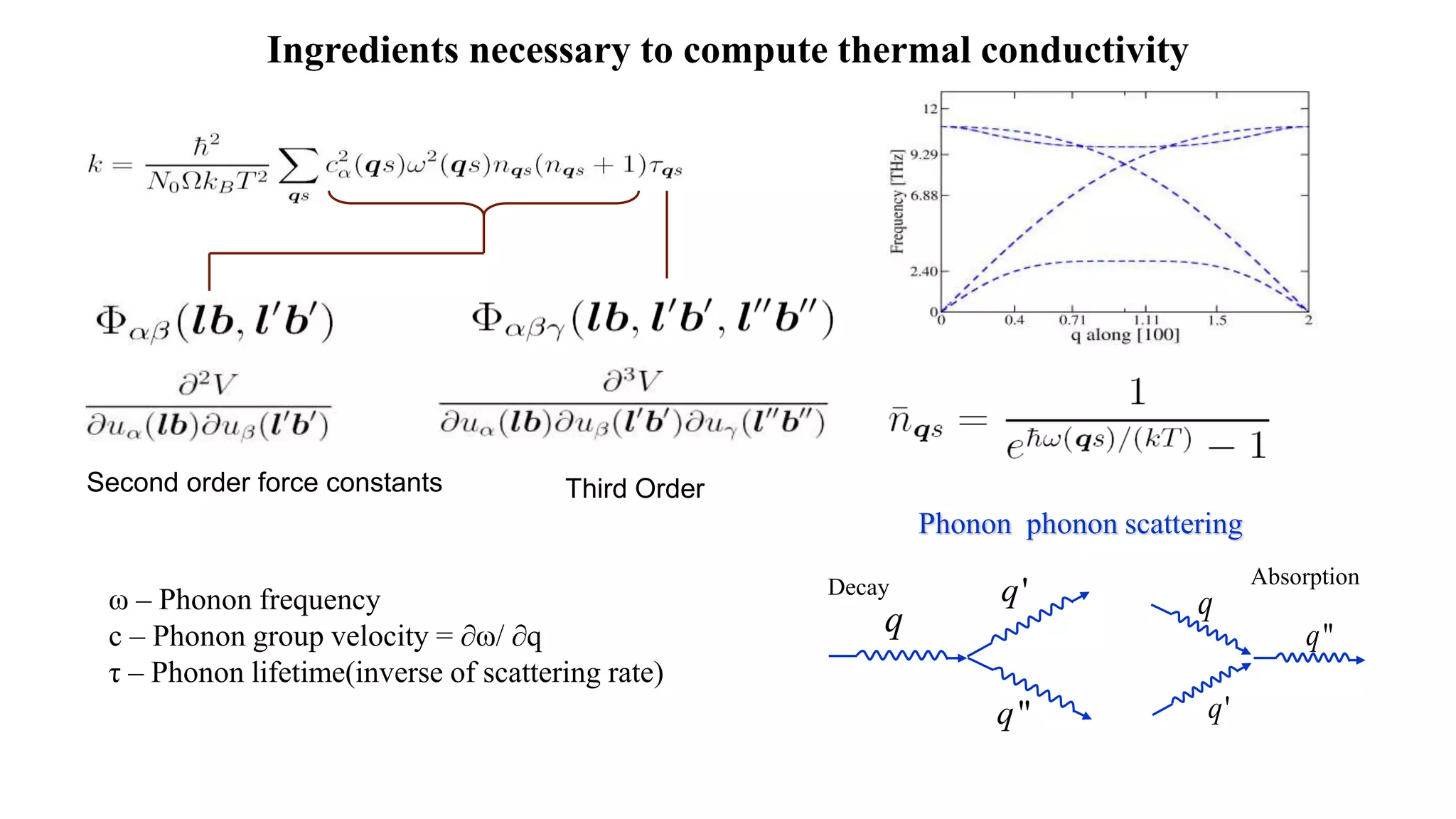
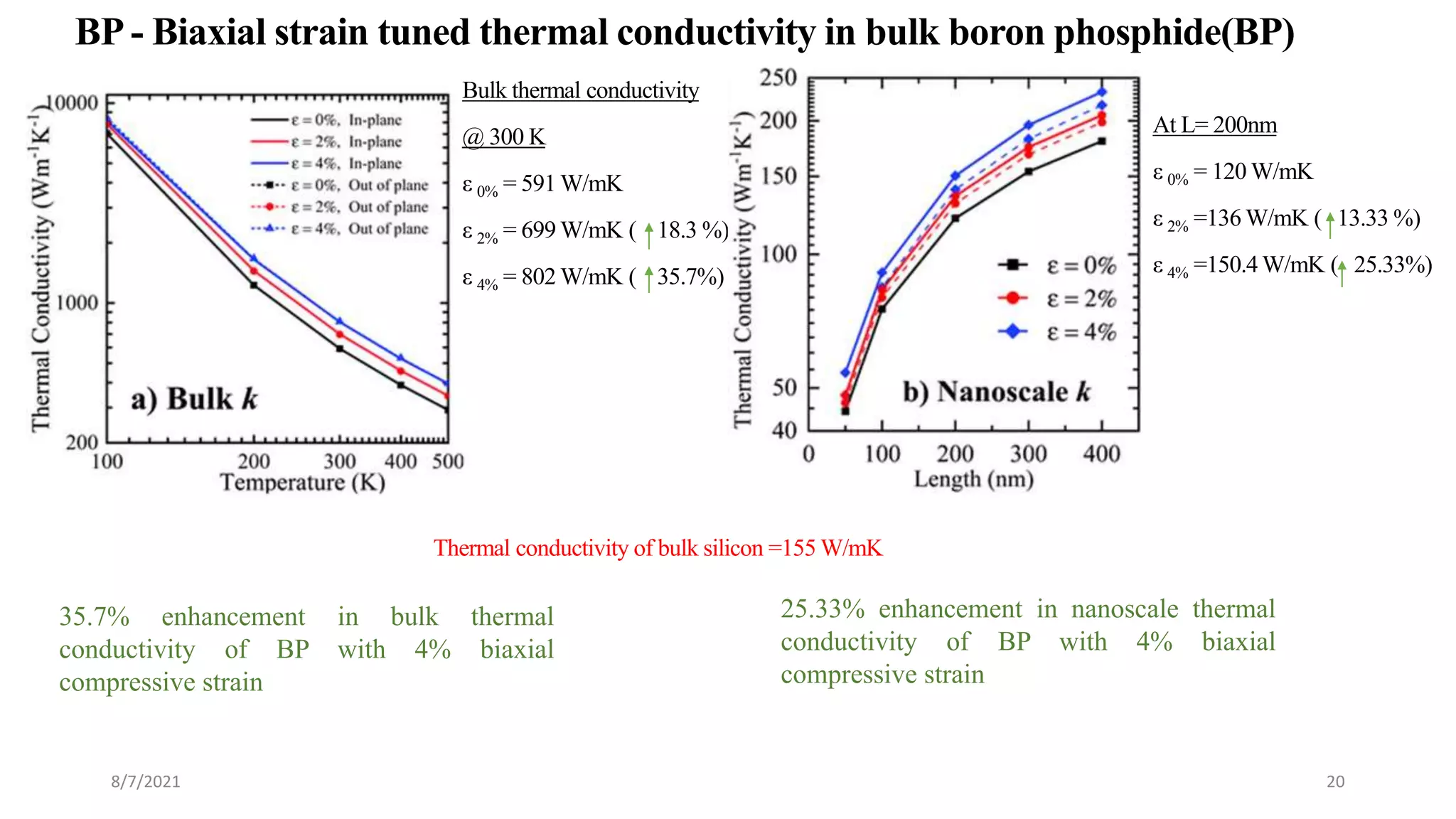
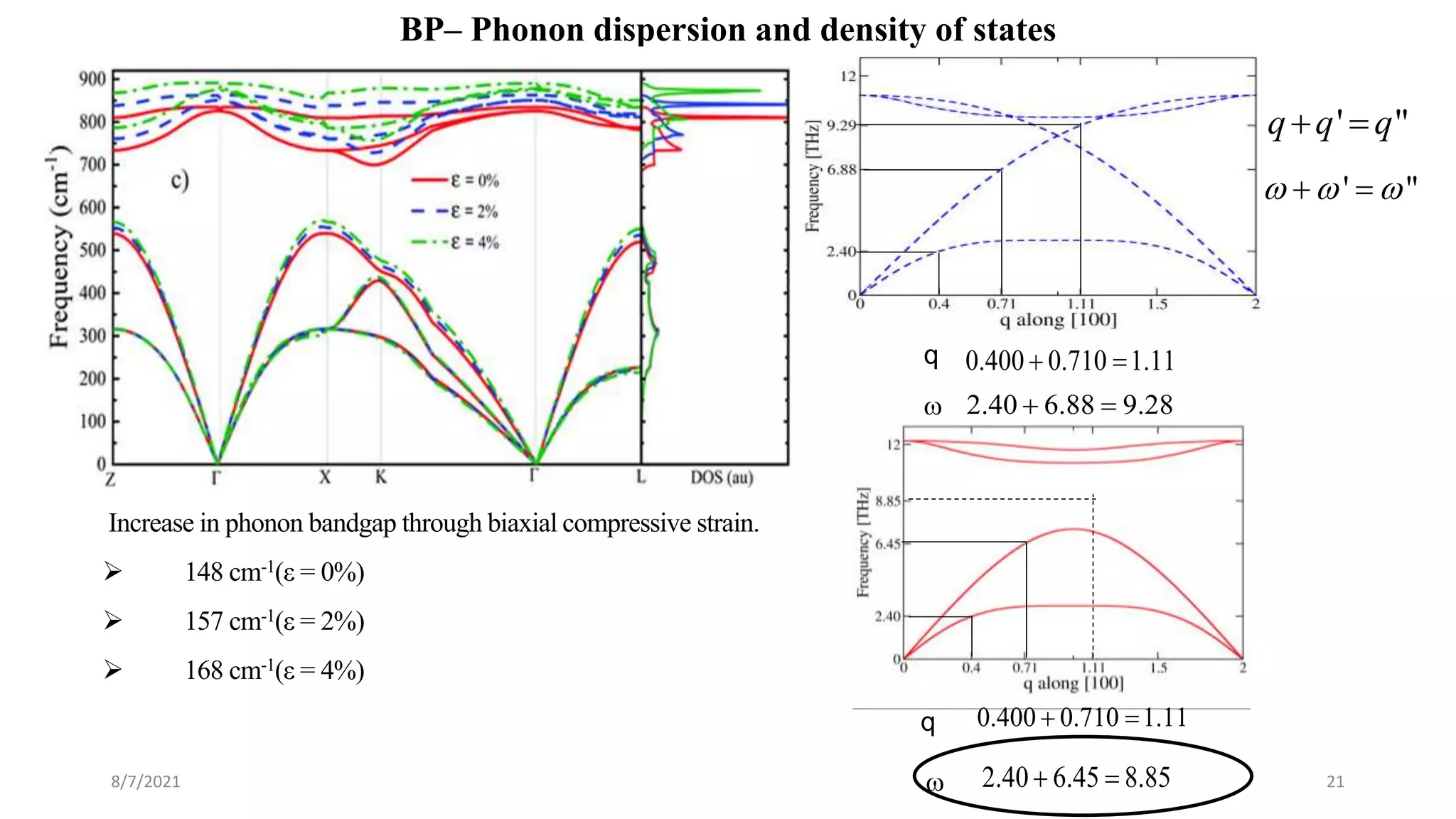
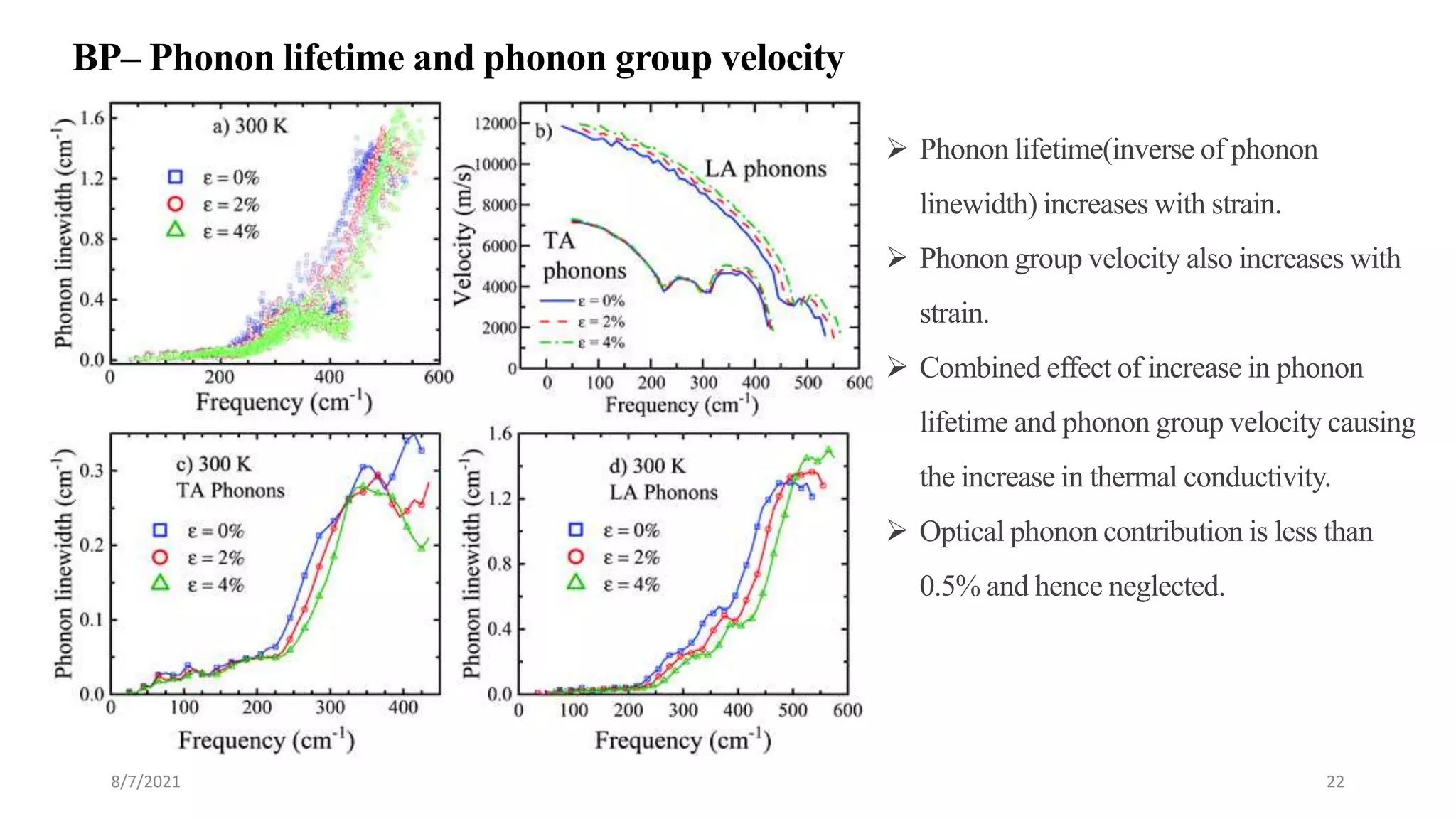
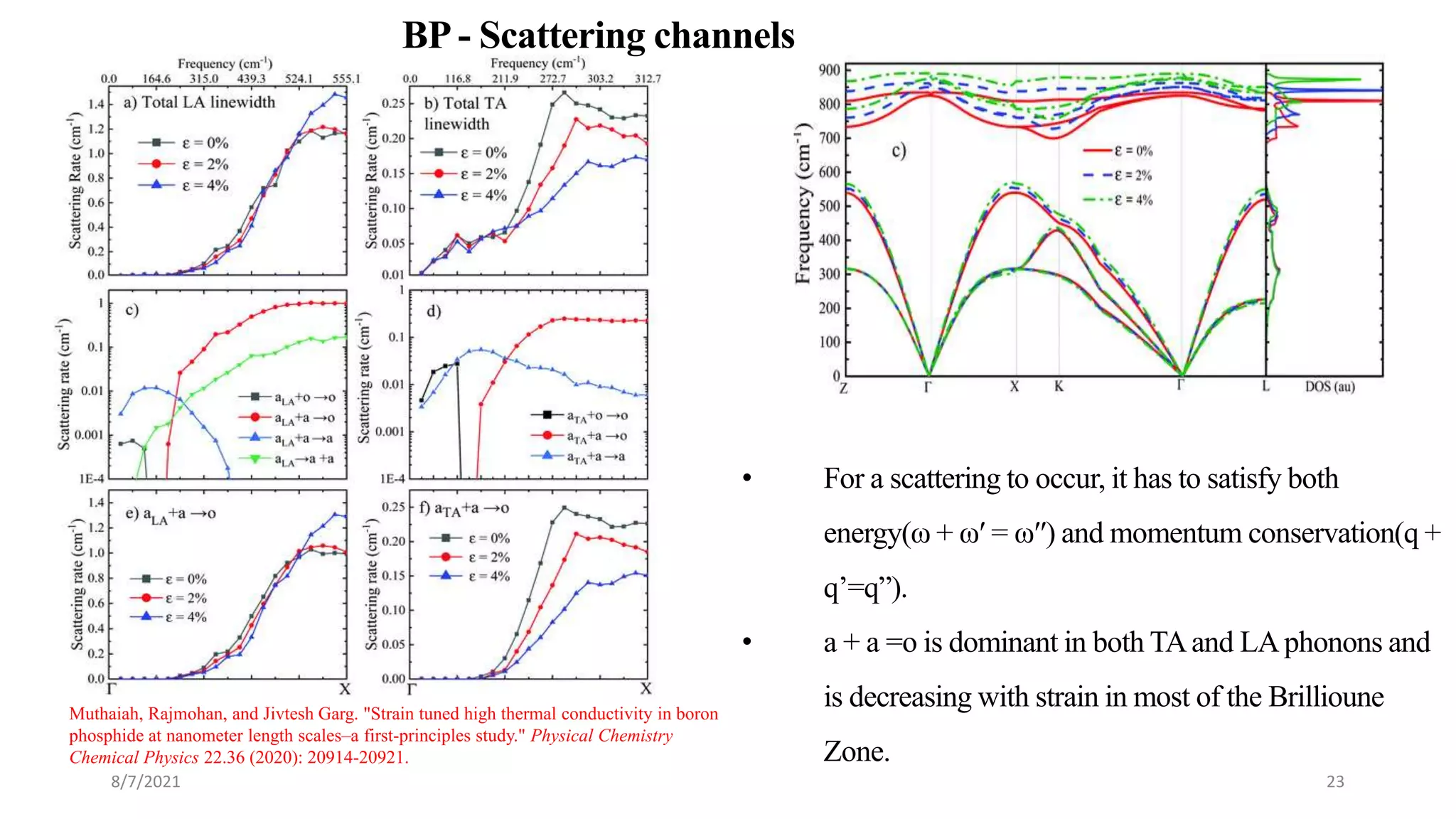
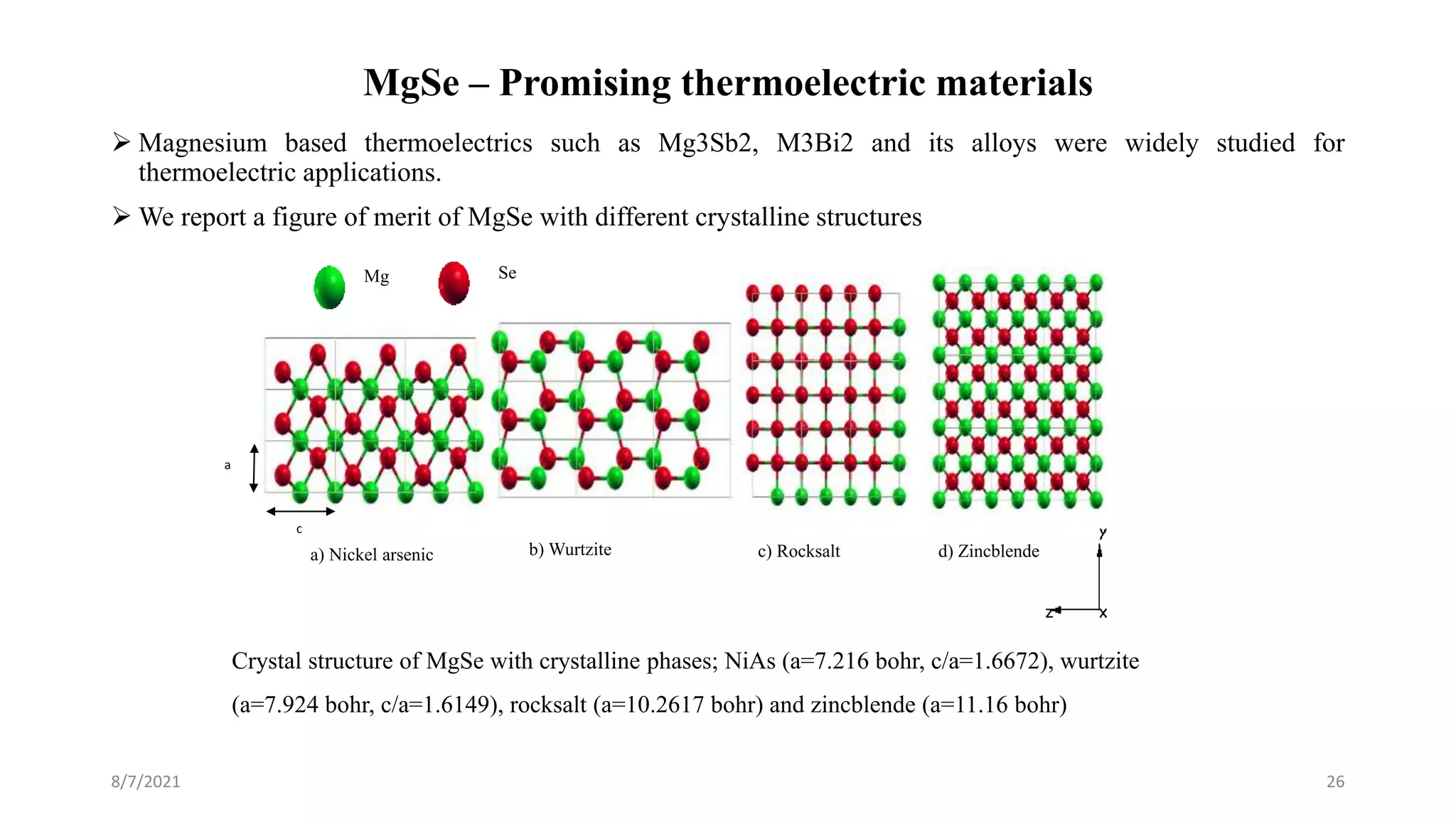
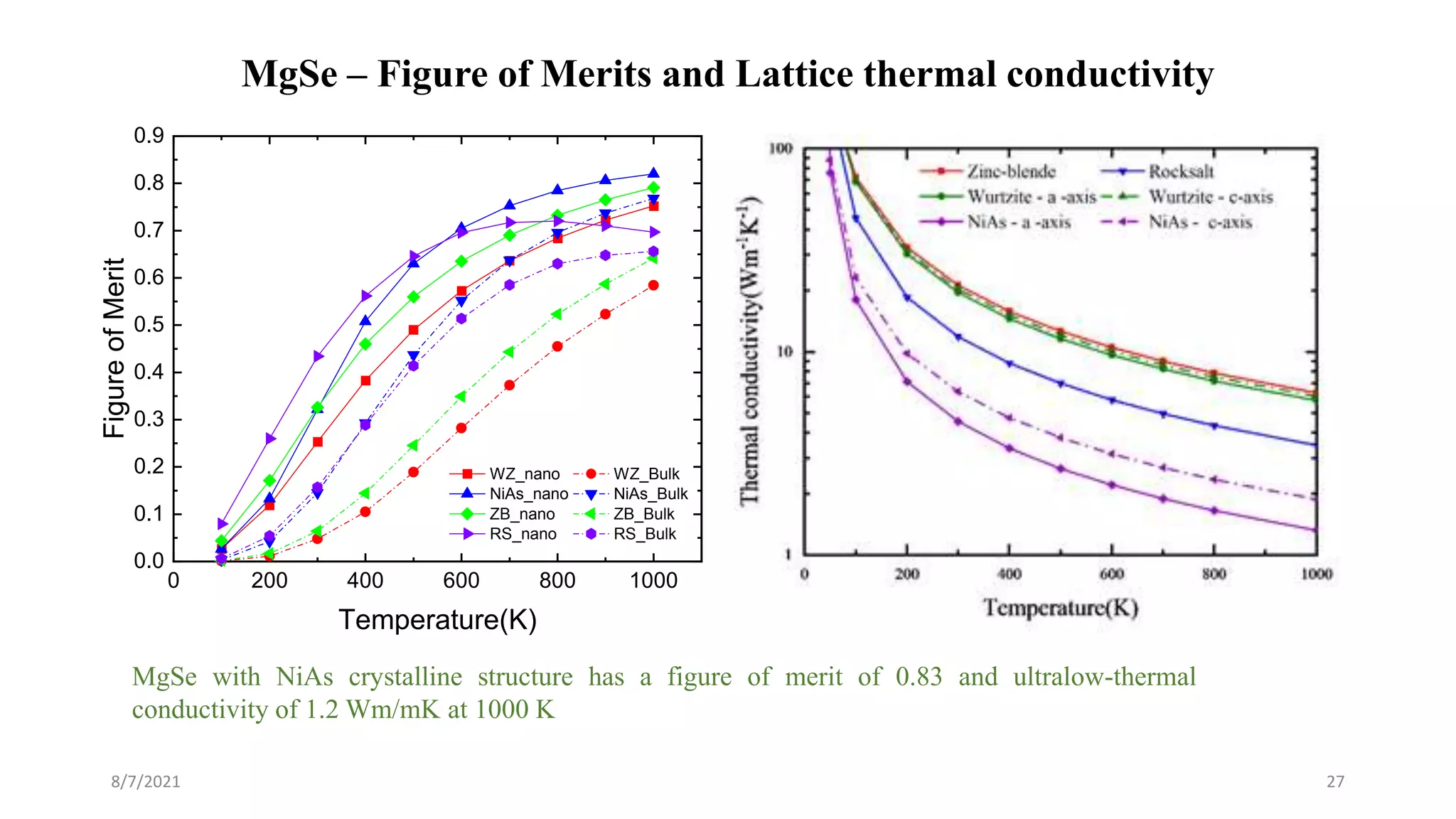
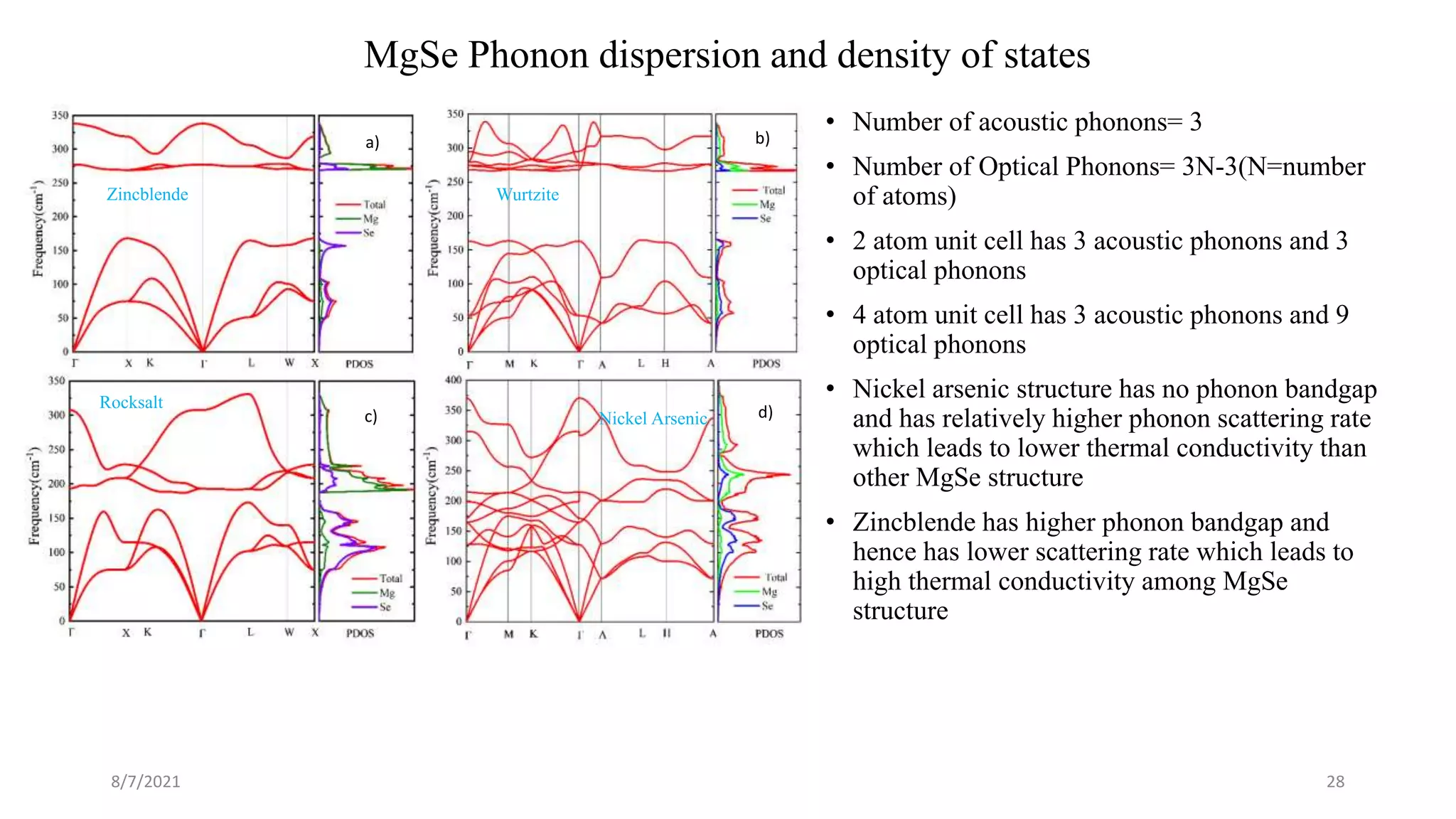
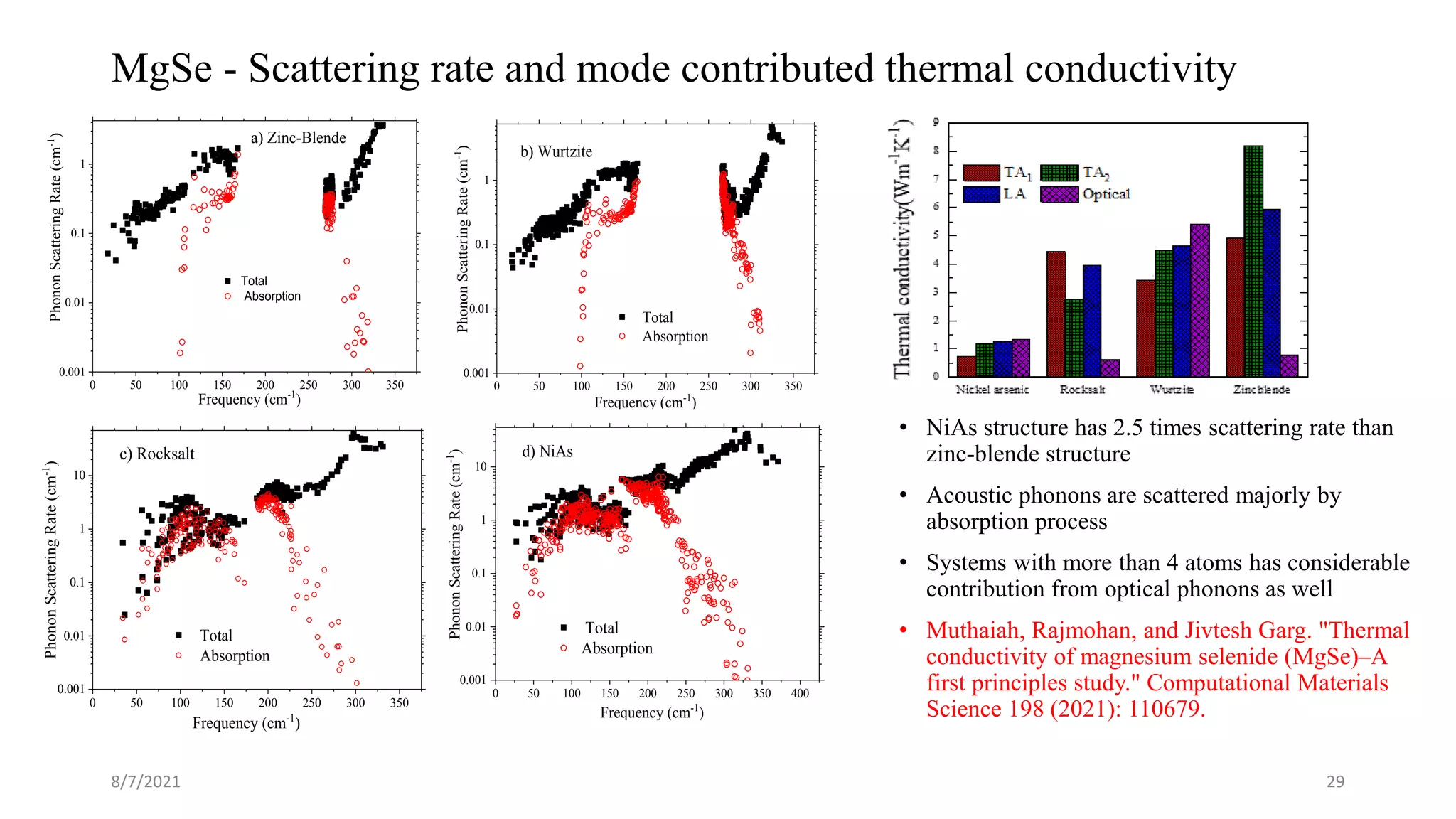
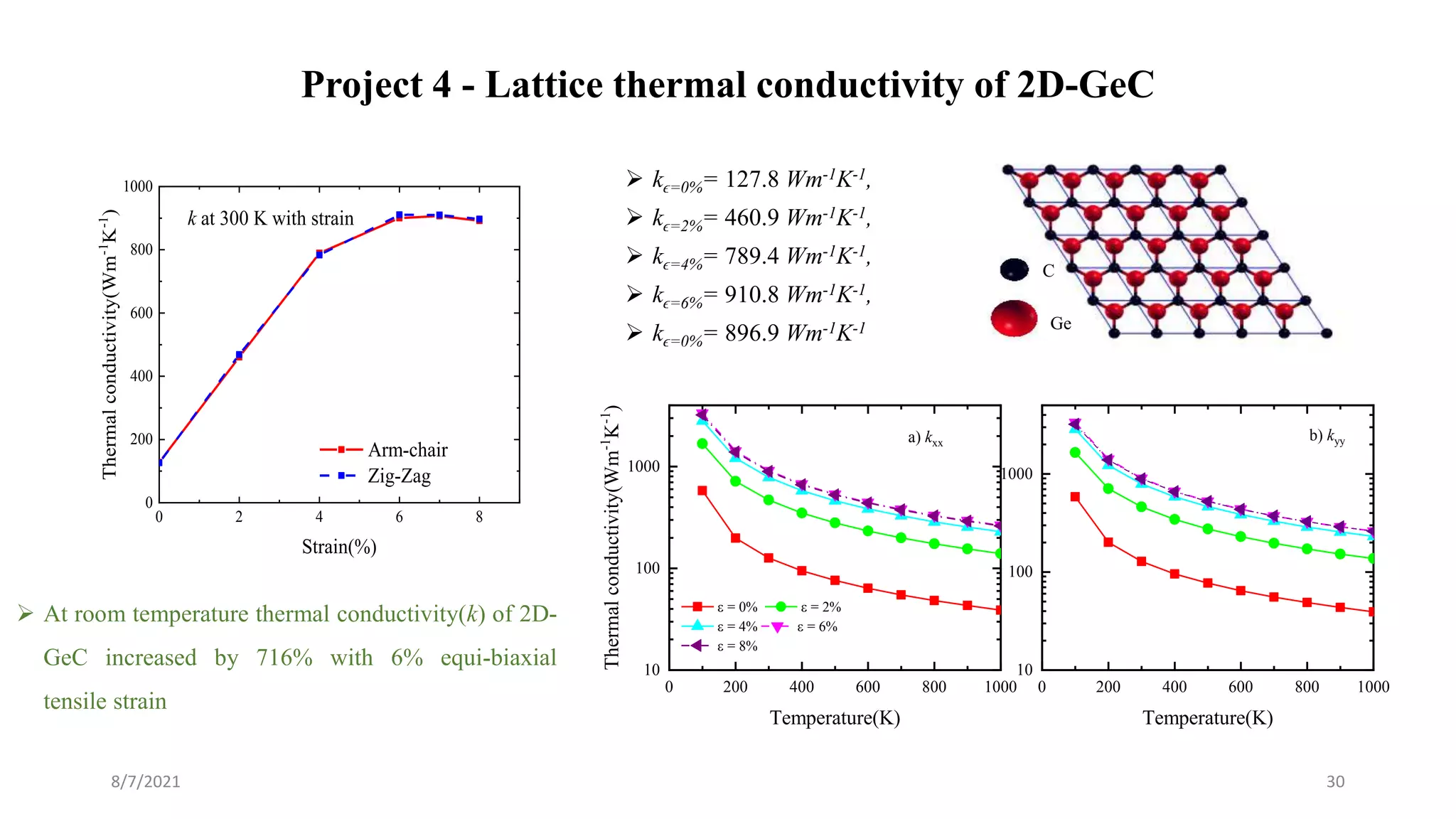
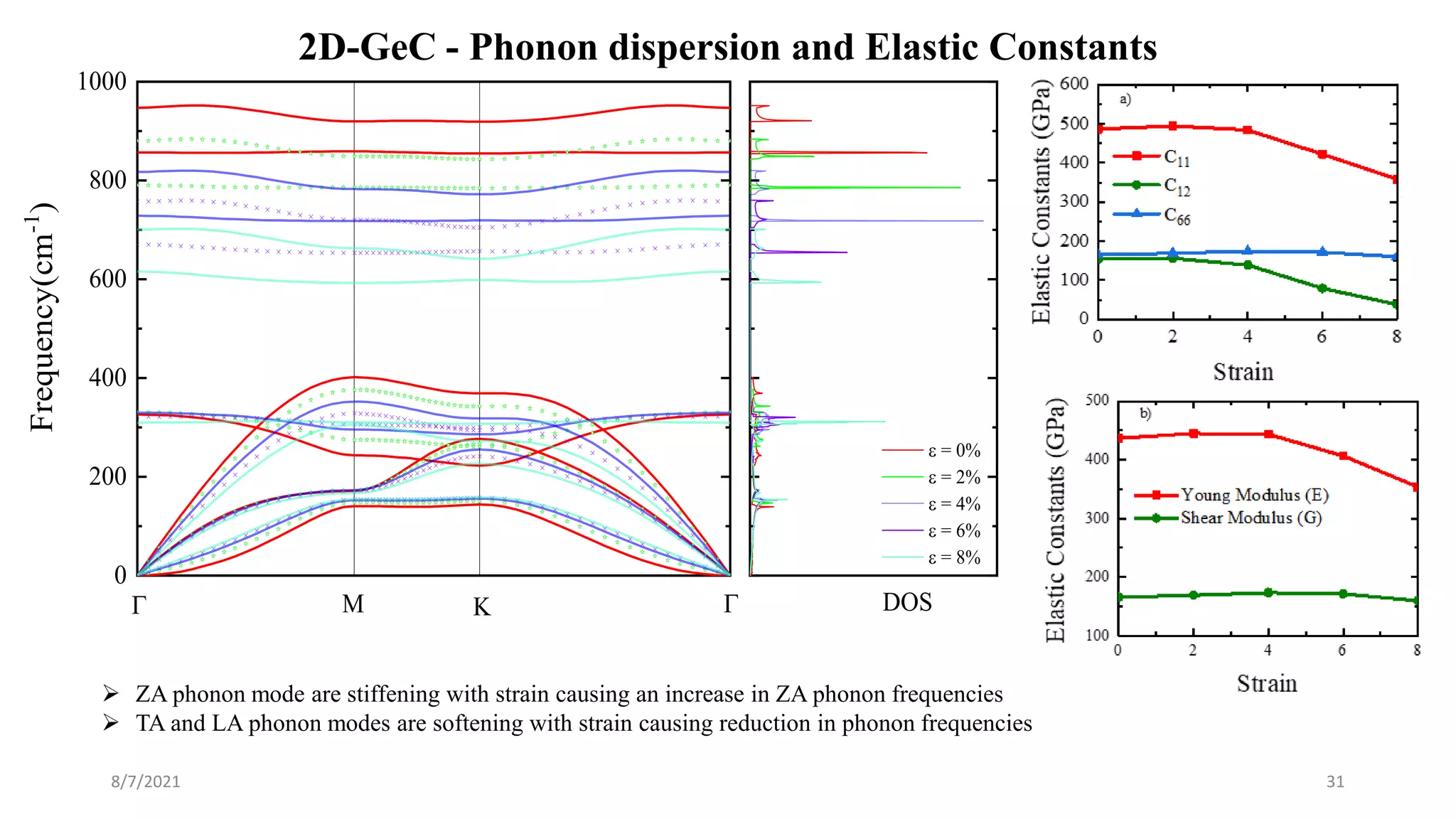
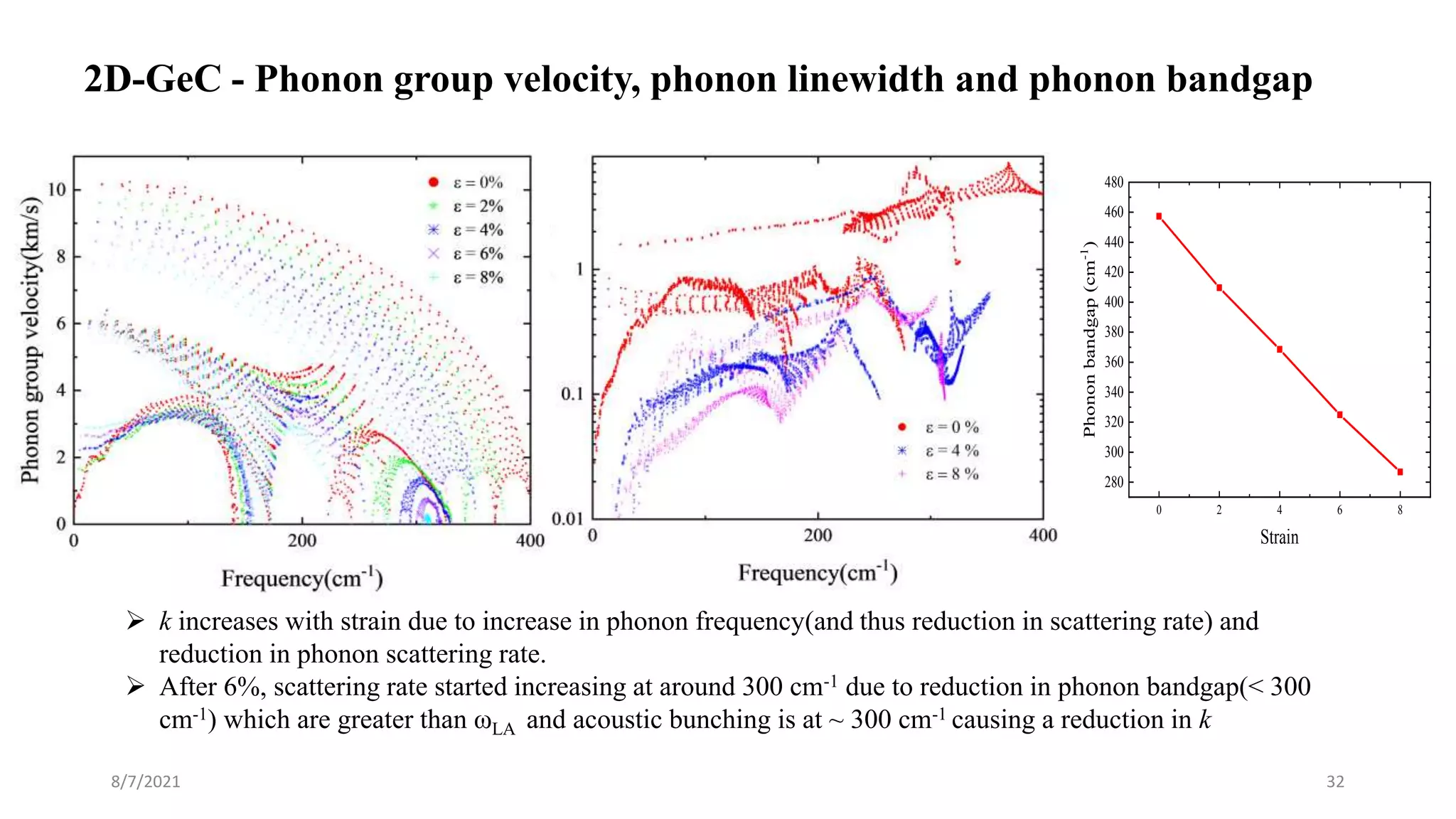
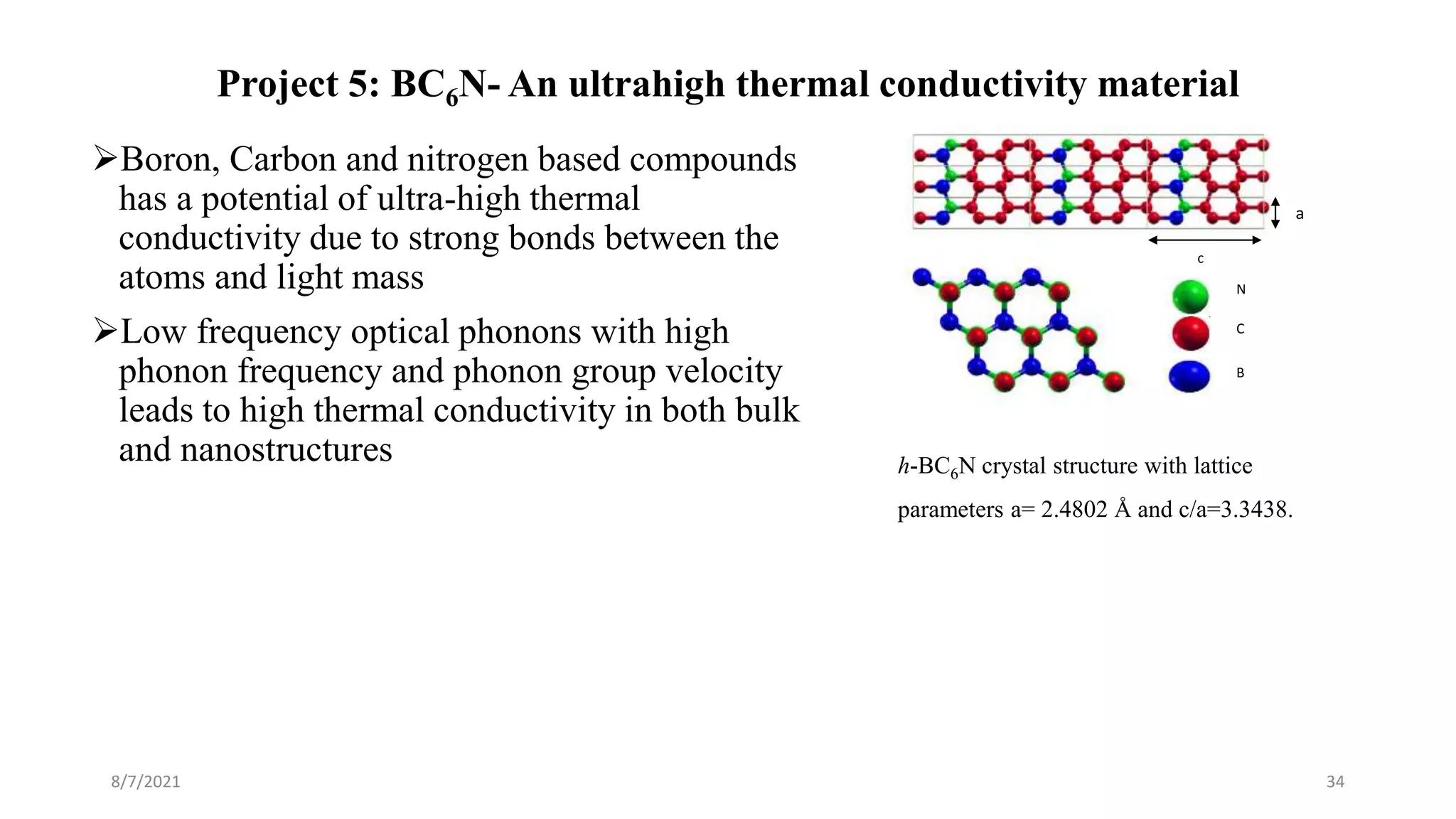
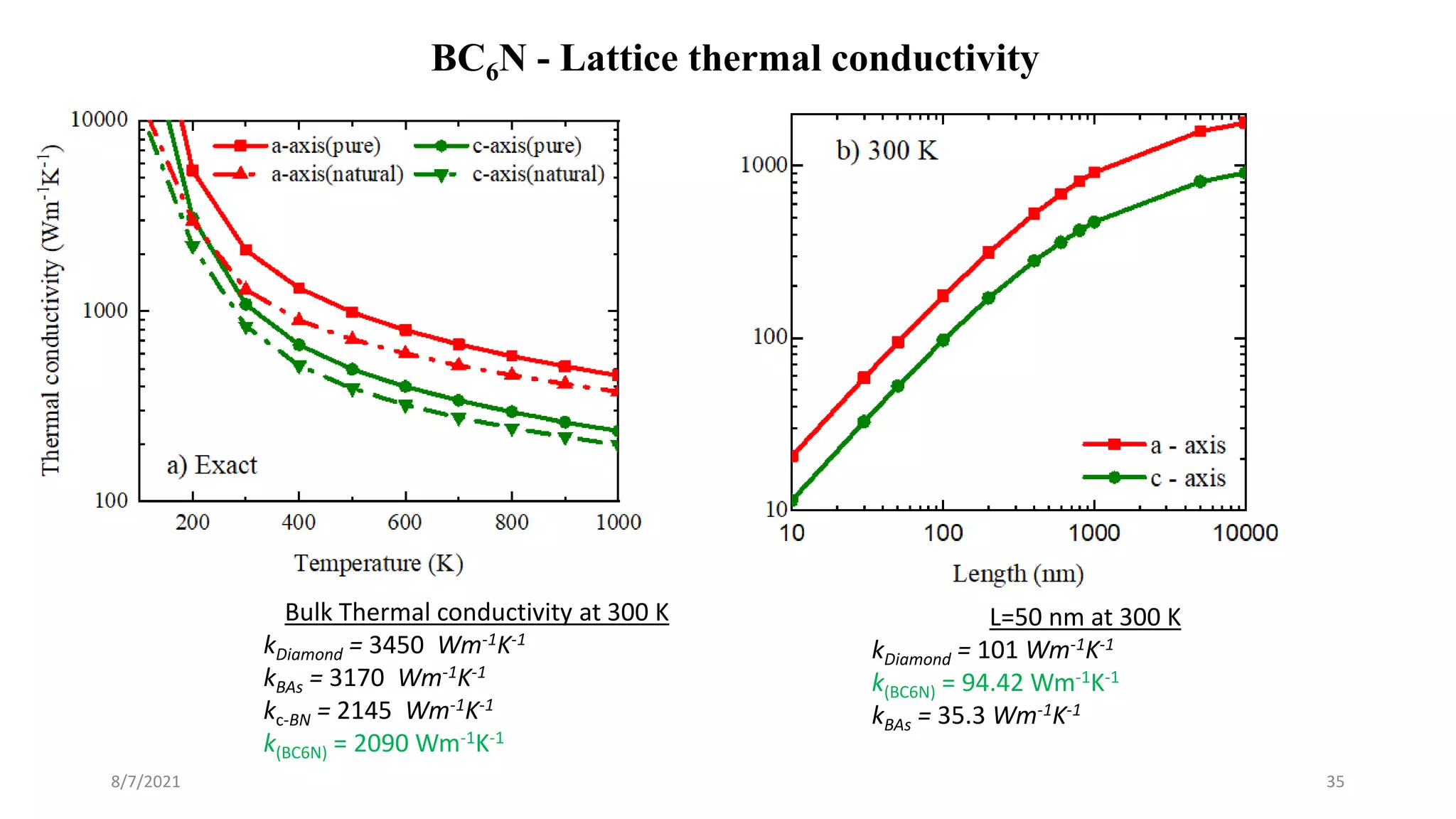
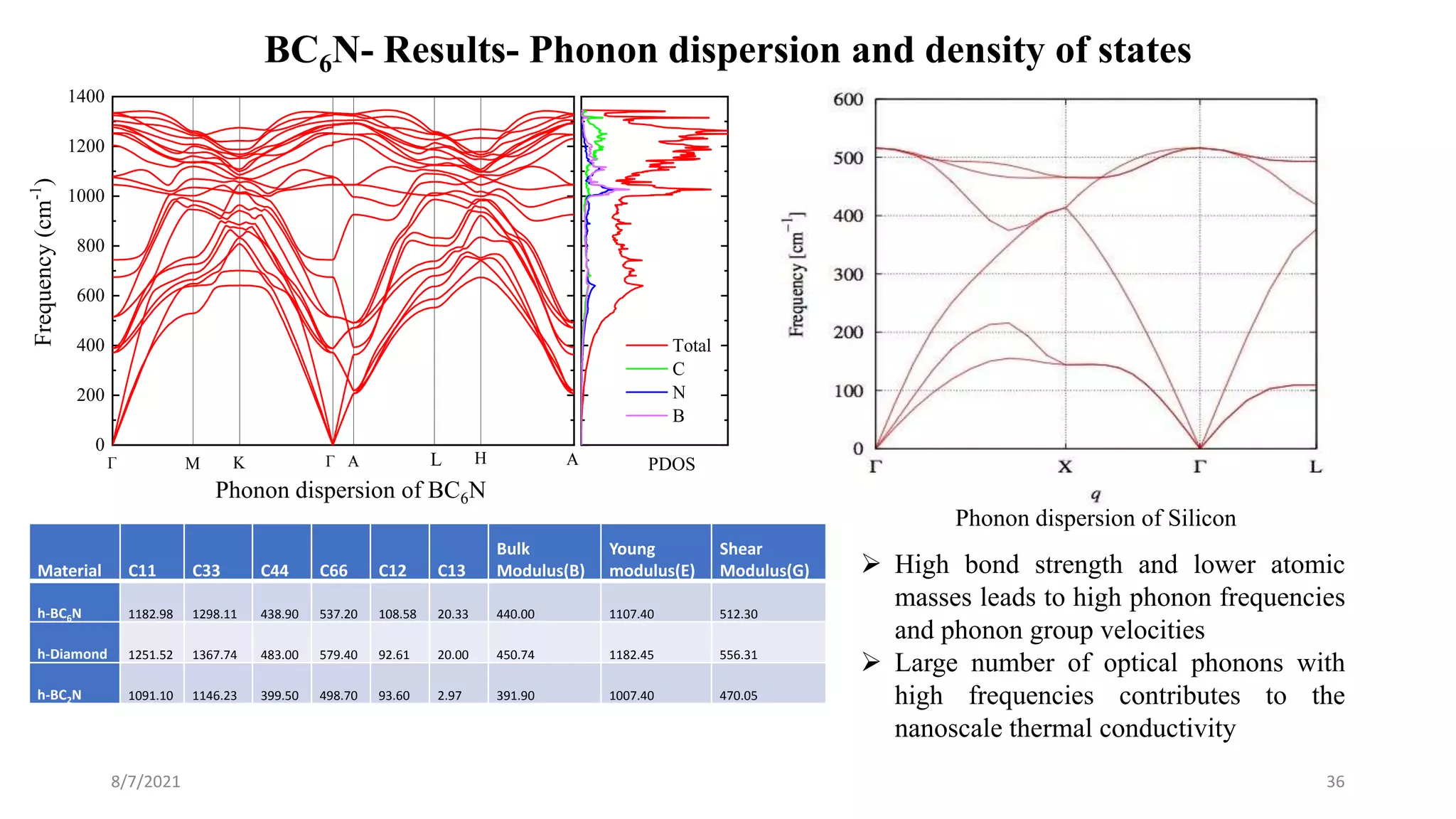
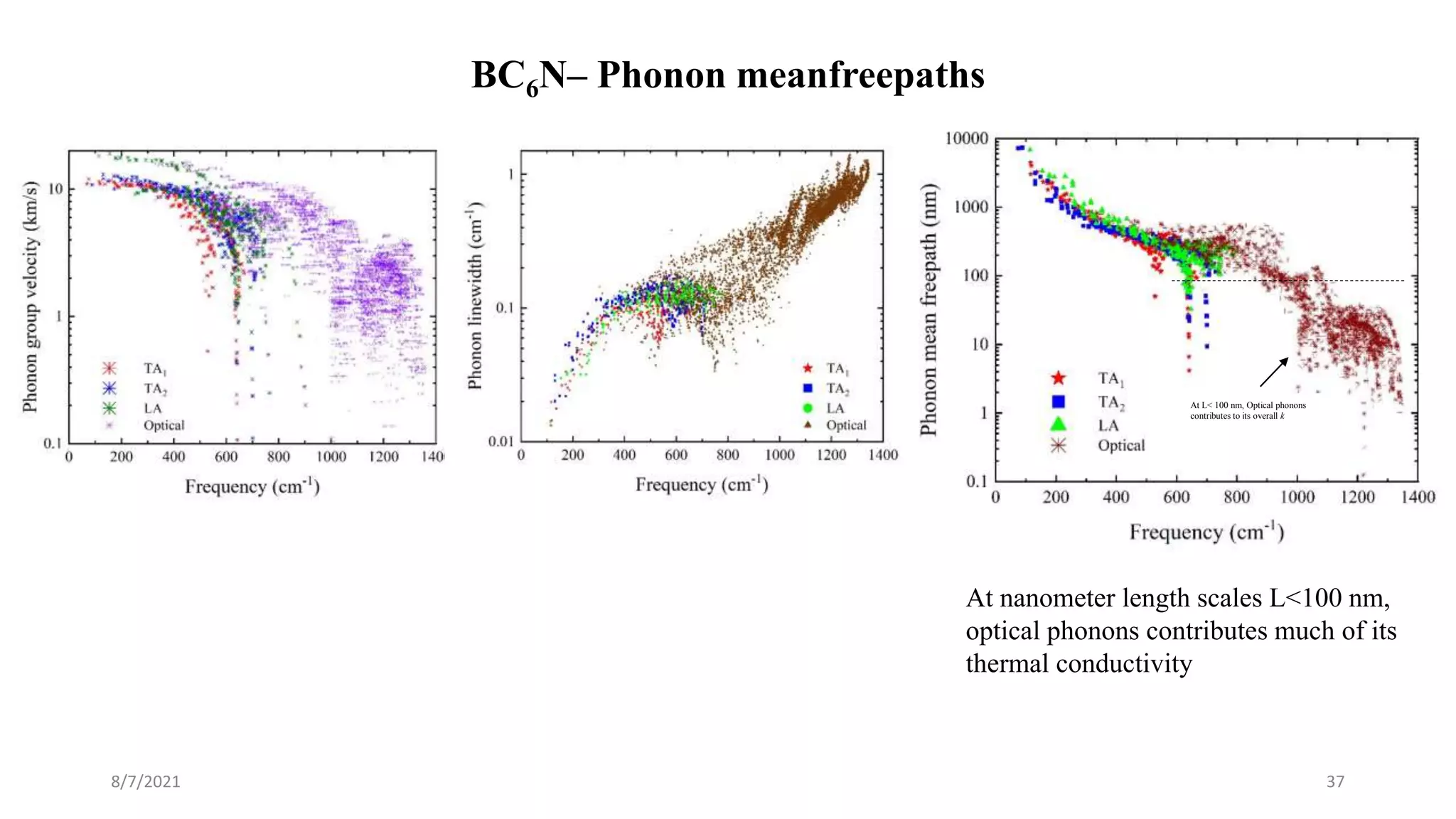
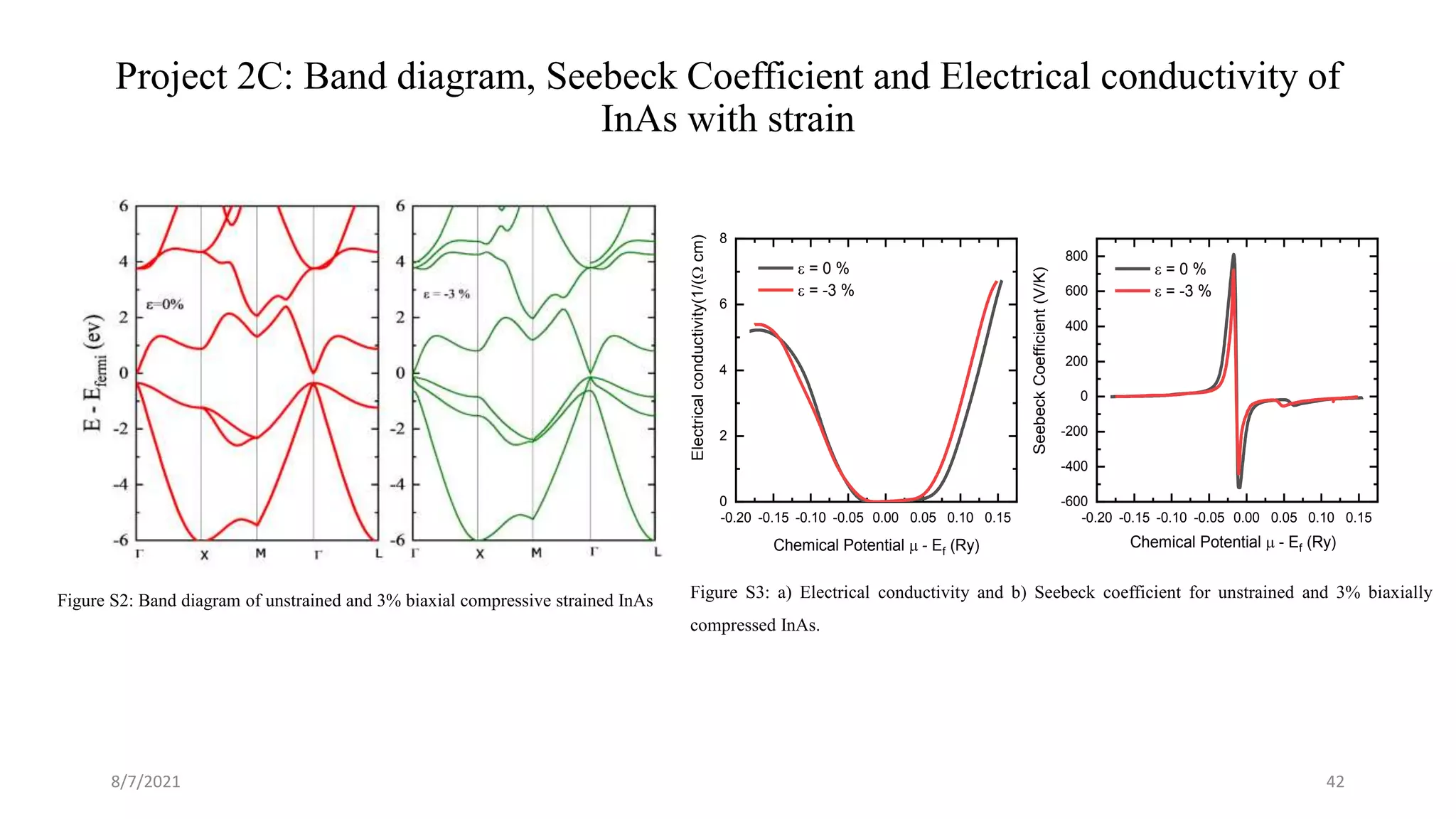
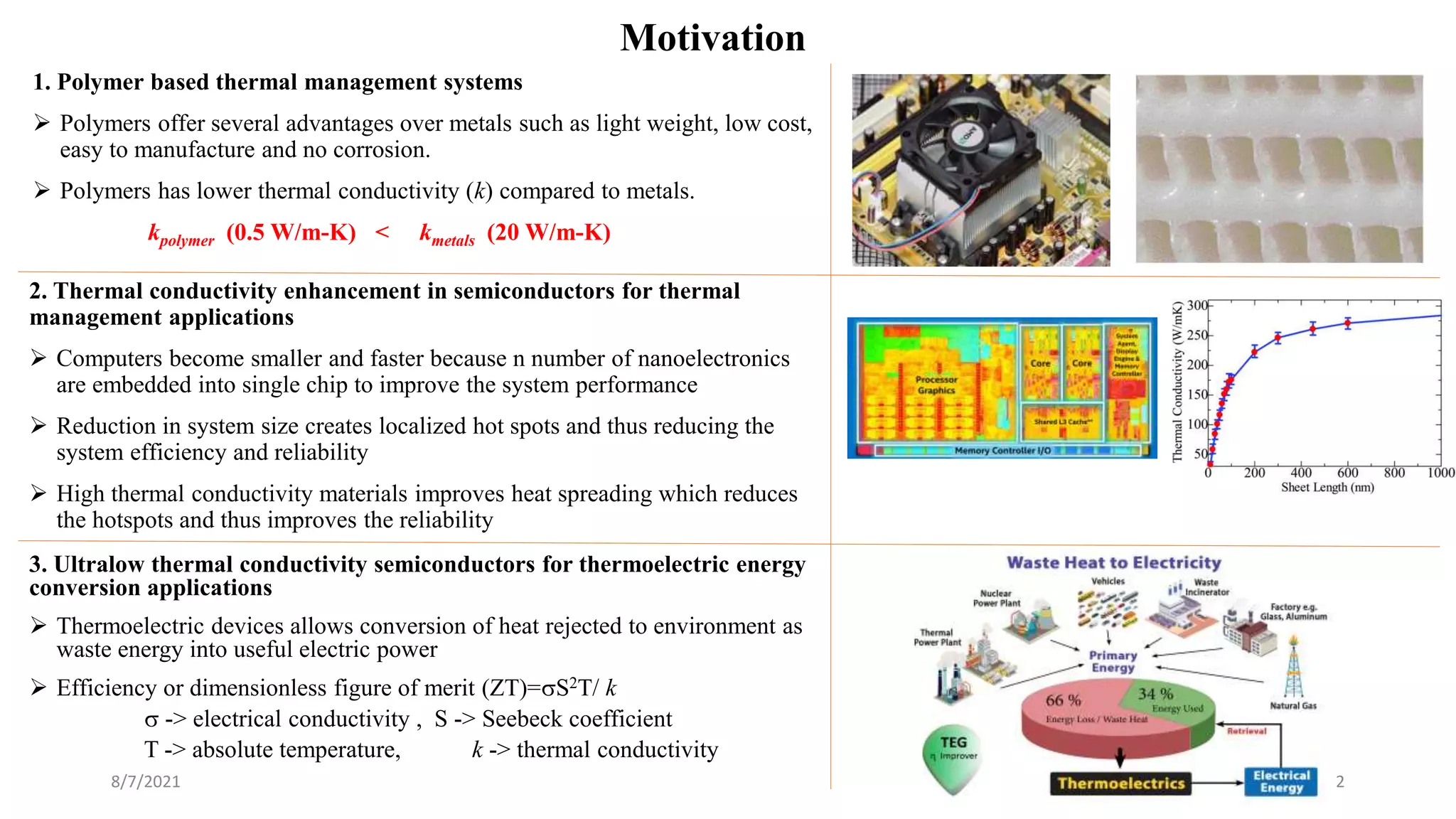
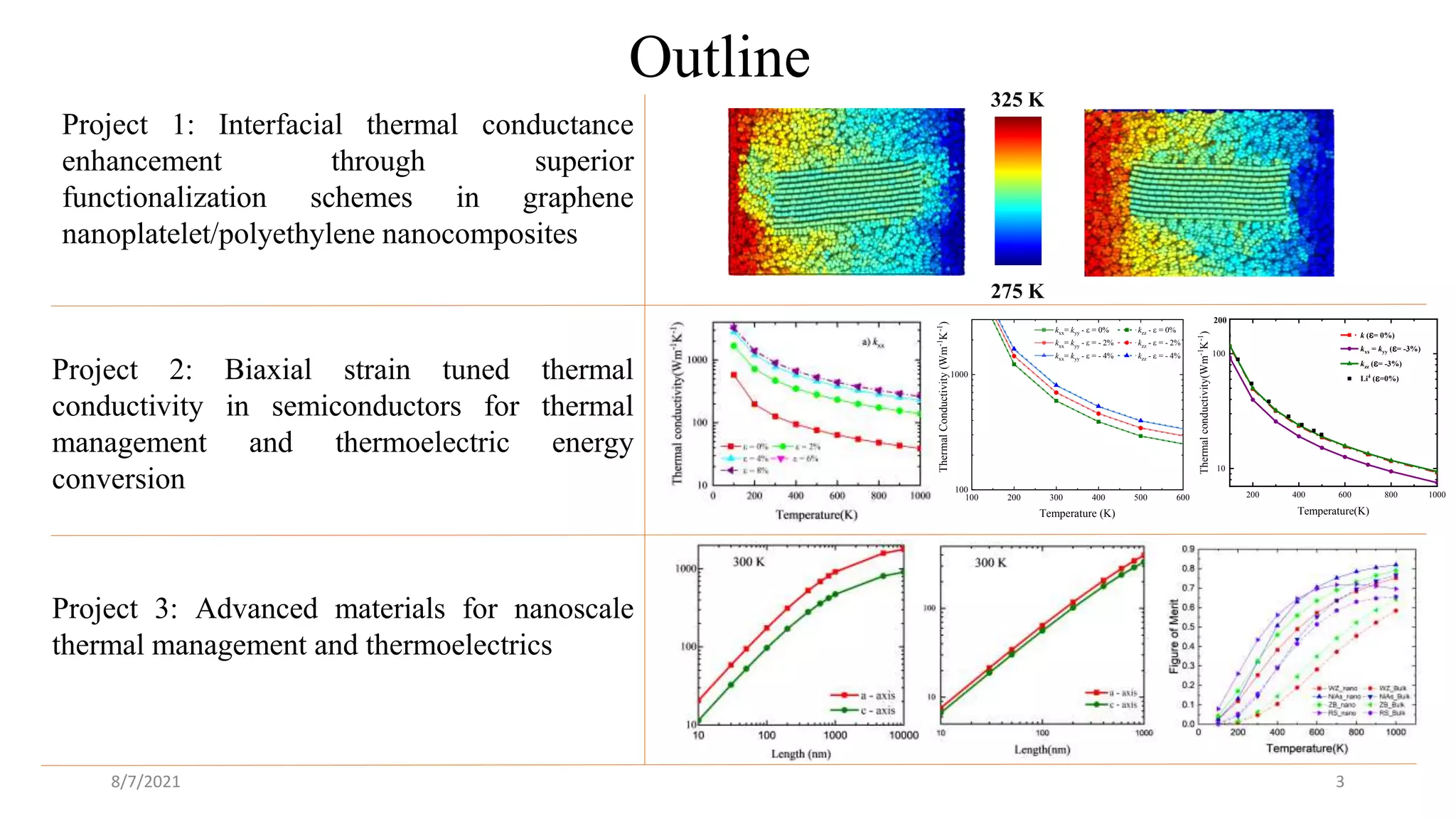
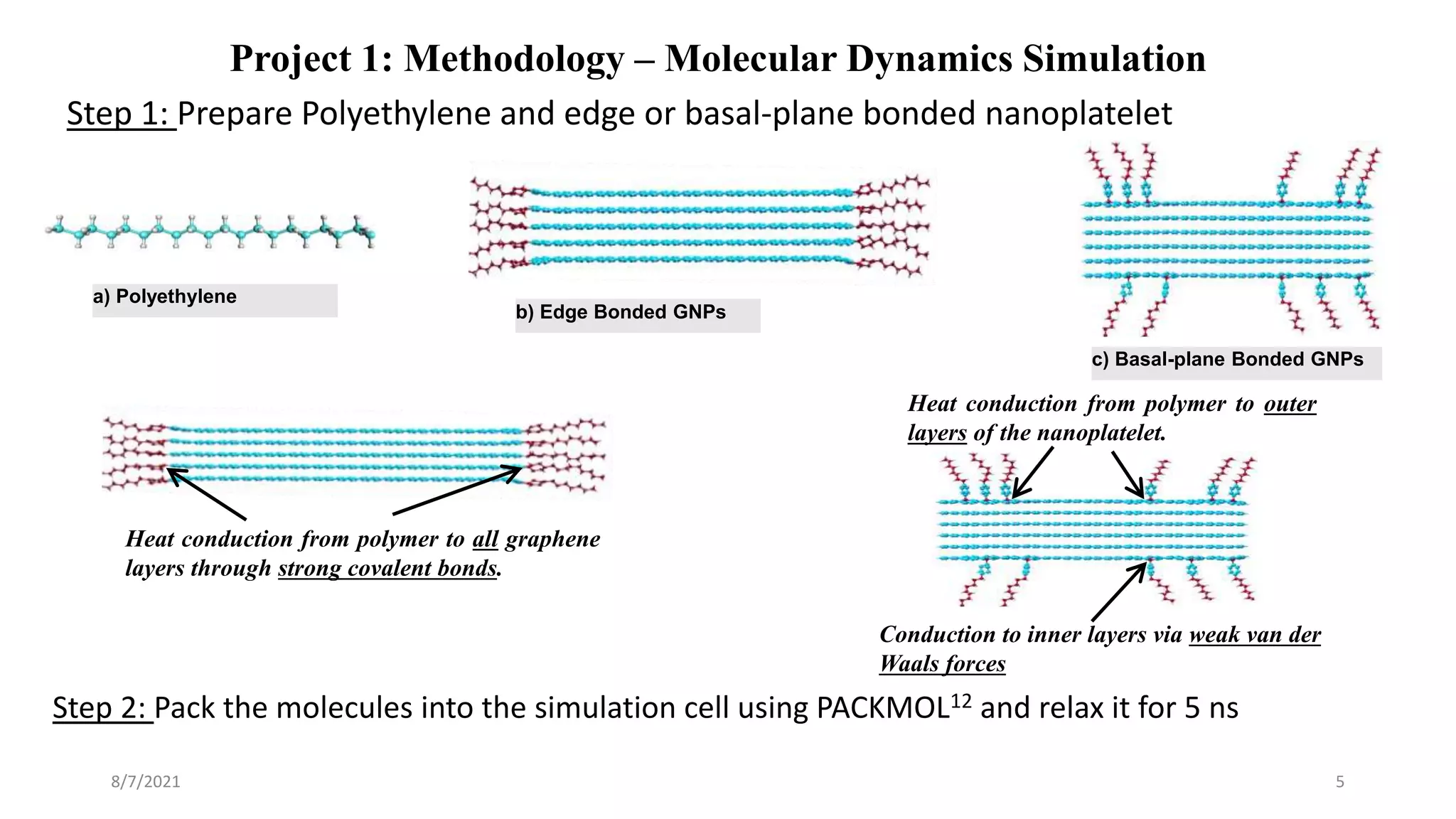
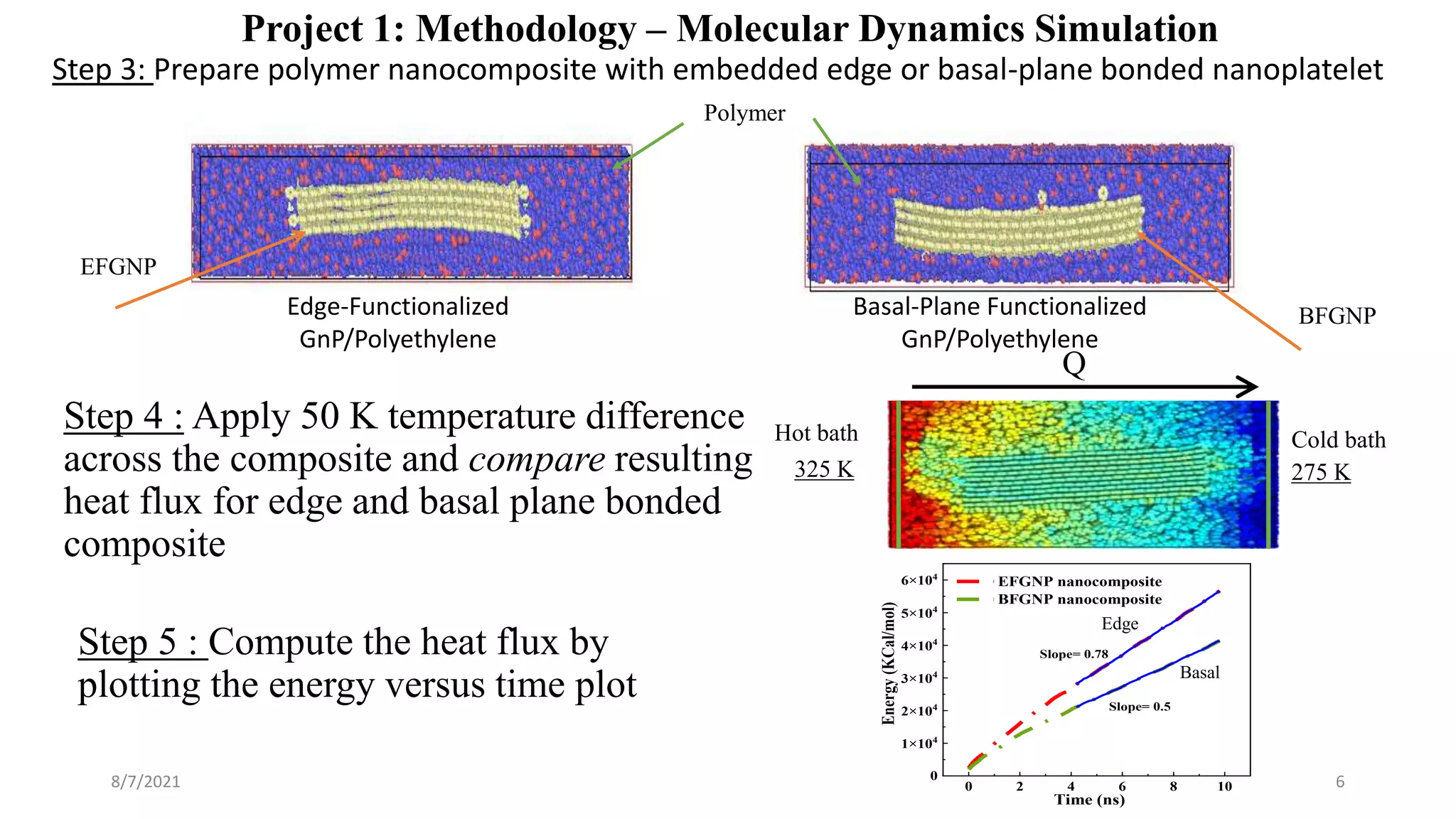
This document discusses the enhancement of thermal transport in polymers, polymer nanocomposites, and semiconductors using molecular dynamics simulations and first principles studies. It outlines three main projects that focus on interfacial thermal conductance in nanocomposites, the effects of biaxial strain on thermal conductivity in semiconductors, and the development of thermoelectric materials for energy conversion. The overall goal is to improve thermal management systems by utilizing advanced materials and methodologies to enhance thermal conductivity and system performance.

1. THERMAL TRANSPORT IN POLYMERS, POLYMER
NANOCOMPOSITES AND SEMICONDUCTORS
USING MOLECULAR DYNAMICS SIMULATION AND
FIRST PRINCIPLES STUDY
Rajmohan Muthaiah, PhD Candidate
Advisor: Dr. Jivtesh Garg, School of Aerospace and Mechanical
Engineering(AME), The University of Oklahoma.
Committee Members: Dr.Wilson Merchan Merchan (AME)
Dr. Yingtao Liu (AME)
Dr. Hamidreza Shabgard (AME)
Dr. Liangliang Huang (CBME)
8/7/2021 1

2. Motivation
8/7/2021 2
1. Polymer based thermal management systems
 Polymers offer several advantages over metals such as light weight, low cost,
easy to manufacture and no corrosion.
 Polymers has lower thermal conductivity (k) compared to metals.
kpolymer (0.5 W/m-K) < kmetals (20 W/m-K)
2. Thermal conductivity enhancement in semiconductors for thermal
management applications
 Computers become smaller and faster because n number of nanoelectronics
are embedded into single chip to improve the system performance
 Reduction in system size creates localized hot spots and thus reducing the
system efficiency and reliability
 High thermal conductivity materials improves heat spreading which reduces
the hotspots and thus improves the reliability
3. Ultralow thermal conductivity semiconductors for thermoelectric energy
conversion applications
 Thermoelectric devices allows conversion of heat rejected to environment as
waste energy into useful electric power
 Efficiency or dimensionless figure of merit (ZT)=S2T/ k
 -> electrical conductivity , S -> Seebeck coefficient
T -> absolute temperature, k -> thermal conductivity

3. Outline
8/7/2021 3
Project 1: Interfacial thermal conductance
enhancement through superior
functionalization schemes in graphene
nanoplatelet/polyethylene nanocomposites
325 K
275 K
Project 2: Biaxial strain tuned thermal
conductivity in semiconductors for thermal
management and thermoelectric energy
conversion 100 200 300 400 500 600
100
1000
Thermal
Conductivity
(Wm
-1
K
-1
)
Temperature (K)
kxx= kyy - e = 0% kzz - e = 0%
kxx= kyy - e = - 2% kzz - e = - 2%
kxx= kyy - e = - 4% kzz - e = - 4%
200 400 600 800 1000
10
100
Thermal
conductivity(Wm
-1
K
-1
)
Temperature(K)
k (e= 0%)
kxx = kyy (e= -3%)
kzz (e= -3%)
Li4
(e=0%)
200
Project 3: Advanced materials for nanoscale
thermal management and thermoelectrics

4. Project 1: Interfacial thermal conductance enhancement through superior
functionalization schemes in graphene nanoplatelet/polyethylene nanocomposites
Motivation: Polymers has plenty of advantages over metals such as less weight, easy to fabricate, low cost and no
corrosion and there is a scope for polymers in thermal management applications.
Problem Identification
 Thermal conductivity of polymers are low( kpolymers < 0.5 Wm-1K-1)
 Ultrahigh thermal conductivity(k) materials(Graphene, Boron nitride etc) are embedded into polymers to increase
overall k of nanocomposites
 k1-3
nanocomposites <<< kfillers(Graphene4-6, BN7-8 and BAs9-11 etc) due to poor bonding between the
polymers and fillers and thus vibrational mismatch
Solution:
 Proper coupling between graphene and polymers through functionalization
 We studied the effect of edge and basal plane functionalization on thermal conductivity enhancement in polymer
nanocomposites using molecular dynamics simulation
8/7/2021 4
Interface
Polymer
Graphene

5. Project 1: Methodology – Molecular Dynamics Simulation
8/7/2021 5
Step 1: Prepare Polyethylene and edge or basal-plane bonded nanoplatelet
Step 2: Pack the molecules into the simulation cell using PACKMOL12 and relax it for 5 ns
b) GNPs
a) Polyethylene
c) Basal-plane Bonded GNPs
b) Edge Bonded GNPs
Heat conduction from polymer to all graphene
layers through strong covalent bonds.
Heat conduction from polymer to outer
layers of the nanoplatelet.
Conduction to inner layers via weak van der
Waals forces

6. Project 1: Methodology – Molecular Dynamics Simulation
Step 4 : Apply 50 K temperature difference
across the composite and compare resulting
heat flux for edge and basal plane bonded
composite
8/7/2021 6
Step 5 : Compute the heat flux by
plotting the energy versus time plot
0 2 4 6 8 10
0
1×104
2×104
3×104
4×104
5×104
6×104
Energy
(KCal/mol)
Time (ns)
EFGNP nanocomposite
BFGNP nanocomposite
Slope= 0.78
Slope= 0.5
Edge
Basal
325 K 275 K
Q
Hot bath Cold bath
Edge-Functionalized
GnP/Polyethylene
Basal-Plane Functionalized
GnP/Polyethylene
Step 3: Prepare polymer nanocomposite with embedded edge or basal-plane bonded nanoplatelet
Polymer
EFGNP
BFGNP

7. Molecular Dynamics Simulation - Background
What is molecular dynamics (MD)?
Molecular dynamics (MD) is a computer simulation
method for studying the physical movements of
atoms and molecules
Basic idea of molecular dynamics:
Solution of Newton’s equations of motion for the
individual particles (atoms, ions, …)
Forces between the particles and their potential
energies are calculated using interatomic potentials
or molecular mechanics force fields
We uses COMPASS force field to define the
interatomic potentials.

8. Bonded Interactions
There are 3 types of interaction
between bonded atoms:
• Stretching along the bond
• Bending between bonds
• Rotating around bonds
bond
along
rotate
bend
angle
stretch
bond
bonded E
E
E
E 


 


Non-Bonded Interactions
There are two potential functions we
need to be concerned about between
non-bonded atoms:
• van der Waals Potential
• Electrostatic Potential
tic
electrosta
Waals
der
van
bonded
non E
E
E 
 



9. Molecular dynamics simulation - Background
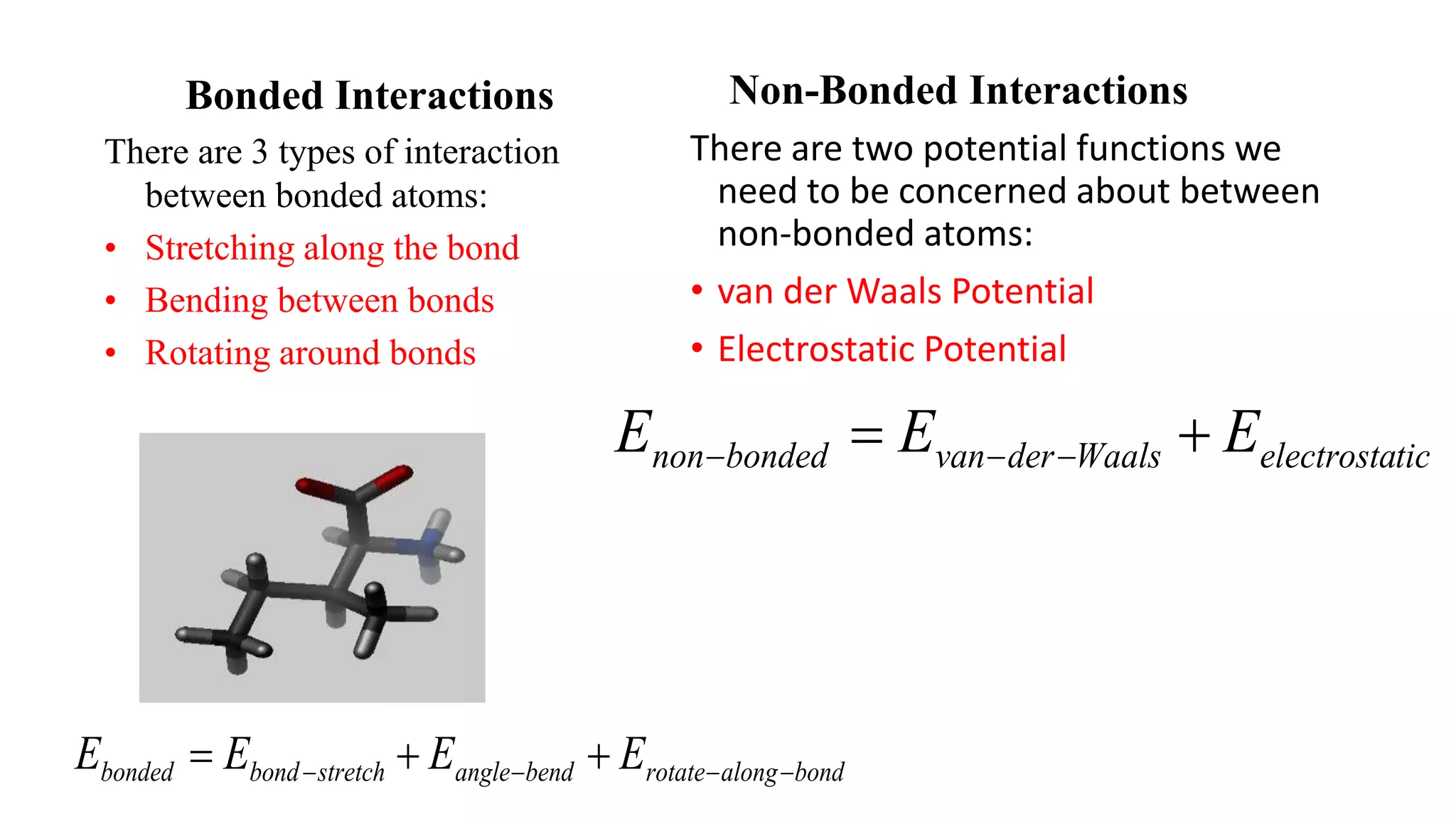
 Derive the force term from its gradient of its potential energy function
8/7/2021
9
 Extract the acceleration using Newton’s law
 To find the position of an atom at t+ Δt, use taylor’s expansion
 When adding the two formulas, the first and third derivatives cancel out:
 And we can express the next timestep in terms of the previous position and the current acceleration:
)
(
)
(
)
(
2
)
(
)
( 4
2
t
O
t
t
a
t
r
t
t
r
t
t
r 









)
(
)
(
)
(
)
(
2
)
( 4
2
t
O
t
t
a
t
t
r
t
r
t
t
r 









)
(
)]
(
)
(
[
2
1
)
( 2
t
O
t
t
r
t
t
r
t
t
v 








 Velocity of an atom can be calculated using the finite difference method

10. Project 1: Results – MD Simulation
8/7/2021 10
325 K
275 K
4 5 6 7 8 9 10
1.20
1.25
1.30
1.35
1.40
1.45
1.50
Heat
flux
ratio
Number of Sheets
QEdge/QBasal
a) Edge bonding b) Basal-Plane bonding Results clearly
demonstrate
more efficient
thermal
transport for
edge bonding
case

11. Single nanoplatelet Calculations
• Single nanoplatelet calculations clearly indicates that edge functionalization
outperforms basal plane functionalization
8/7/2021 11
Edge
Basal
100 200 300
1
2
3
4
16 layers
4 layers

Q
edge
Q
basal
Nanoplatelet Length (nm)

8 layers

12. Project 1: Results – Single Sheet Calculation
8/7/2021 12
Edge Basal Plane
Large
distortion
Minimal distortion
Temperature distribution along the simulation box in pristine, edge and basal
plane functionalized graphene
Temperature drops due to
distortion at the sp3 site
Edge functionalization
outperform basal plane
functionalization due to
less distortion

13. Project 1- Take away
We reported superior thermal transport in polymer/graphene
nanoplatelet nanocomposites through a novel edge functionalization
of graphene nanoplatelets.
Inner layers of edge functionalized GNPs are actively participating
in heat conduction than the inner layers of basal plane functionalized
GNPs
Edge functionalization leads to less distortion than basal plane
functionalization indicating less damage to the graphene
8/7/2021 13

14. Project 2a: Biaxial strain tuned thermal conductivity enhancement in
semiconductors for thermal management
Motivation : We can expect the speed and capability of our
computers to increase every couple of years, and we will pay less
for them – Moore’s Law.
Computers become smaller and faster because n number of
nanoelectronics are embedded into single chip to improve the
system performance.
Problem: Thermal conductivity decreases with reduction in
system size due to phonon boundary scattering.
Opportunity: There is a strong need for an increase in thermal
conductivity at nanoscale to improve the system performance and
reliability.
8/7/2021 14

15. Background
 Phonons are the primary heat carriers.
 Lattice vibrations and interactions between them determine the
thermal transport in semiconductors
 Heat dissipation depends on how fast(velocity and frequency) and
how far(mean free path) a phonon can travel without any
disturbance(scattering).
 Materials with light mass and strong bond has high thermal
conductivity due to high frequency and phonon group velocity.
Example, Graphene and diamond has a thermal conductivity over
3500 W/mK.
 Materials with phonon bandgap has high thermal conductivity
(Si=155 W/mK, BAs = 3500 W/mK) due to suppression of
scattering rate by optical phonons.
8/7/2021 15
Optical phonons
Acoustic phonons
Acoustic Optical

16. Thermal conductivity calculation- Boltzmann Transport equation
Boltzmann Transport Equation
Bose Einstein Distribution
High T High n
Low T Low n

17. Thermal conductivity calculation- Boltzmann Transport equation

18. Ingredients necessary to compute thermal conductivity
Second order force constants Third Order
ω – Phonon frequency
c – Phonon group velocity = ∂ω/ ∂q
τ – Phonon lifetime(inverse of scattering rate)
'
q
q
"
q
q
'
q
"
q
Phonon phonon scattering
Decay Absorption

19. BP- Biaxial strain tuned thermal conductivity in bulk boron
phosphide(BP) - Methodology
8/7/2021 19
• Density functional theory coupled with PBTE using
QUANTUM ESPRESSO Package
• LDA and norm-conserving pseudopotentials
• 12 x 12 x 12 k-point mesh to integrate the Brillouin zone
• 8 x 8 x 8 mesh to compute 2nd order force constants and
phonon dispersion
• 4 x 4 x 4 mesh to compute 3rd order force constants using
QE-D3Q package
• k calculations on 30 x 30 x 30 with 0.1 cm-1 smearing

20. BP - Biaxial strain tuned thermal conductivity in bulk boron phosphide(BP)
Thermal conductivity of bulk silicon =155 W/mK
Bulk thermal conductivity
@ 300 K
ε 0% = 591 W/mK
ε 2% = 699 W/mK ( 18.3 %)
ε 4% = 802 W/mK ( 35.7%)
At L= 200nm
ε 0% = 120 W/mK
ε 2% =136 W/mK ( 13.33 %)
ε 4% =150.4 W/mK ( 25.33%)
8/7/2021 20
35.7% enhancement in bulk thermal
conductivity of BP with 4% biaxial
compressive strain
25.33% enhancement in nanoscale thermal
conductivity of BP with 4% biaxial
compressive strain

21. BP– Phonon dispersion and density of states
8/7/2021 21
Increase in phonon bandgap through biaxial compressive strain.
 148 cm-1(ε = 0%)
 157 cm-1(ε = 2%)
 168 cm-1(ε = 4%)
0.400 0.710 1.11
 
q
2.40 6.88 9.28
 

' "
q q q
 
' "
  
 
0.400 0.710 1.11
 
q
2.40 6.45 8.85
 


22.  Phonon lifetime(inverse of phonon
linewidth) increases with strain.
 Phonon group velocity also increases with
strain.
 Combined effect of increase in phonon
lifetime and phonon group velocity causing
the increase in thermal conductivity.
 Optical phonon contribution is less than
0.5% and hence neglected.
BP– Phonon lifetime and phonon group velocity
8/7/2021 22

23. • For a scattering to occur, it has to satisfy both
energy(ω + ω′ = ω′′) and momentum conservation(q +
q’=q”).
• a + a =o is dominant in both TAand LAphonons and
is decreasing with strain in most of the Brillioune
Zone.
BP - Scattering channels
8/7/2021 23
Muthaiah, Rajmohan, and Jivtesh Garg. "Strain tuned high thermal conductivity in boron
phosphide at nanometer length scales–a first-principles study." Physical Chemistry
Chemical Physics 22.36 (2020): 20914-20921.

24. Boron Phosphide – Take away
• Bulk thermal conductivity of BP increases by ~35% with 4% biaxial
compressive strain
• Nanoscale thermal conductivity of BP increases by ~25% with 4%
strain
• Increase in k is due to the reduction in phonon scattering rate arising
from increase in phonon bandgap as well as increase in phonon group
velocity
8/7/2021 24

25. Project 3- Thermoelectric energy conversion - Background
Thermoelectric materials are capable of converting heat into electric current through Seebeck effect
Efficiency or dimensionless figure of merit (ZT)=S2T/ k
 -> electrical conductivity
S -> Seebeck coefficient
T -> absolute temperature
k -> thermal conductivity
ZT can be increased by either increasing power factor (S2) or by reducing the thermal
conductivity
Key strategy to improve figure of merit without affecting electrical conductivity and Seebeck
coefficient is to reduce the lattice thermal conductivity
Hence, reduction in k leads to increase in ZT.
8/7/2021 25

26. MgSe – Promising thermoelectric materials
8/7/2021 26
 Magnesium based thermoelectrics such as Mg3Sb2, M3Bi2 and its alloys were widely studied for
thermoelectric applications.
 We report a figure of merit of MgSe with different crystalline structures
d) Zincblende
c) Rocksalt
b) Wurtzite
a) Nickel arsenic
Mg Se
Crystal structure of MgSe with crystalline phases; NiAs (a=7.216 bohr, c/a=1.6672), wurtzite
(a=7.924 bohr, c/a=1.6149), rocksalt (a=10.2617 bohr) and zincblende (a=11.16 bohr)
a
c

27. MgSe – Figure of Merits and Lattice thermal conductivity
8/7/2021 27
0 200 400 600 800 1000
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Figure
of
Merit
Temperature(K)
WZ_nano WZ_Bulk
NiAs_nano NiAs_Bulk
ZB_nano ZB_Bulk
RS_nano RS_Bulk
MgSe with NiAs crystalline structure has a figure of merit of 0.83 and ultralow-thermal
conductivity of 1.2 Wm/mK at 1000 K

28. MgSe Phonon dispersion and density of states
• Number of acoustic phonons= 3
• Number of Optical Phonons= 3N-3(N=number
of atoms)
• 2 atom unit cell has 3 acoustic phonons and 3
optical phonons
• 4 atom unit cell has 3 acoustic phonons and 9
optical phonons
• Nickel arsenic structure has no phonon bandgap
and has relatively higher phonon scattering rate
which leads to lower thermal conductivity than
other MgSe structure
• Zincblende has higher phonon bandgap and
hence has lower scattering rate which leads to
high thermal conductivity among MgSe
structure
8/7/2021 28
a) b)
c)
d)
a) b)
c) d)
Rocksalt
Zincblende Wurtzite
Nickel Arsenic

29. MgSe - Scattering rate and mode contributed thermal conductivity
• NiAs structure has 2.5 times scattering rate than
zinc-blende structure
• Acoustic phonons are scattered majorly by
absorption process
• Systems with more than 4 atoms has considerable
contribution from optical phonons as well
• Muthaiah, Rajmohan, and Jivtesh Garg. "Thermal
conductivity of magnesium selenide (MgSe)–A
first principles study." Computational Materials
Science 198 (2021): 110679.
8/7/2021 29
0 50 100 150 200 250 300 350 400
0.001
0.01
0.1
1
10
Total
Absorption
Phonon
Scattering
Rate
(cm
-1
)
Frequency (cm-1
)
d) NiAs
0 50 100 150 200 250 300 350
0.001
0.01
0.1
1
Total
Absorption
Phonon
Scattering
Rate
(cm
-1
)
Frequency (cm-1
)
a) Zinc-Blende
0 50 100 150 200 250 300 350
0.001
0.01
0.1
1
Total
Absorption
Phonon
Scattering
Rate
(cm
-1
)
Frequency (cm-1
)
b) Wurtzite
0 50 100 150 200 250 300 350
0.001
0.01
0.1
1
10
Total
Absorption
Phonon
Scattering
Rate
(cm
-1
)
Frequency (cm-1
)
c) Rocksalt

30. Project 4 - Lattice thermal conductivity of 2D-GeC
8/7/2021 30
0 2 4 6 8
0
200
400
600
800
1000
Thermal
conductivity(Wm
-1
K
-1
)
Strain(%)
Arm-chair
Zig-Zag
k at 300 K with strain
 At room temperature thermal conductivity(k) of 2D-
GeC increased by 716% with 6% equi-biaxial
tensile strain
0 200 400 600 800 1000
10
100
1000
0 200 400 600 800 1000
10
100
1000
Thermal
conductivity(Wm
-1
K
-1
)
Temperature(K)
e = 0% e = 2%
e = 4% e = 6%
e = 8%
a) kxx
Temperature(K)
b) kyy
 kϵ=0%= 127.8 Wm-1K-1,
 kϵ=2%= 460.9 Wm-1K-1,
 kϵ=4%= 789.4 Wm-1K-1,
 kϵ=6%= 910.8 Wm-1K-1,
 kϵ=0%= 896.9 Wm-1K-1 Ge
C

31. 2D-GeC - Phonon dispersion and Elastic Constants
8/7/2021 31
0
200
400
600
800
1000
Frequency(cm
-1
)
e = 0%
e = 2%
e = 4%
e = 6%
e = 8%
G M K G DOS
 ZA phonon mode are stiffening with strain causing an increase in ZA phonon frequencies
 TA and LA phonon modes are softening with strain causing reduction in phonon frequencies

32. 2D-GeC - Phonon group velocity, phonon linewidth and phonon bandgap
8/7/2021 32
0 2 4 6 8
280
300
320
340
360
380
400
420
440
460
480
Phonon
bandgap
(cm
-1
)
Strain
 k increases with strain due to increase in phonon frequency(and thus reduction in scattering rate) and
reduction in phonon scattering rate.
 After 6%, scattering rate started increasing at around 300 cm-1 due to reduction in phonon bandgap(< 300
cm-1) which are greater than ωLA and acoustic bunching is at ~ 300 cm-1 causing a reduction in k

33. 2D-GeC – Take away
• Thermal conductivity(k) can be either increased or decreased
with biaxial strain with strain
• k of monolayer germanium carbide increased by ~ 710 %
with 6 % equi-biaxial strain
• Increase in k is due to an increase in phonon group velocity of
ZA phonon modes and reduction in scattering rate.
8/7/2021 33

34. Project 5: BC6N- An ultrahigh thermal conductivity material
Boron, Carbon and nitrogen based compounds
has a potential of ultra-high thermal
conductivity due to strong bonds between the
atoms and light mass
Low frequency optical phonons with high
phonon frequency and phonon group velocity
leads to high thermal conductivity in both bulk
and nanostructures
8/7/2021 34
N
C
B
a
c
h-BC6N crystal structure with lattice
parameters a= 2.4802 Å and c/a=3.3438.

35. BC6N - Lattice thermal conductivity
8/7/2021 35
Bulk Thermal conductivity at 300 K
kDiamond = 3450 Wm-1K-1
kBAs = 3170 Wm-1K-1
kc-BN = 2145 Wm-1K-1
k(BC6N) = 2090 Wm-1K-1
L=50 nm at 300 K
kDiamond = 101 Wm-1K-1
k(BC6N) = 94.42 Wm-1K-1
kBAs = 35.3 Wm-1K-1

36. BC6N- Results- Phonon dispersion and density of states
8/7/2021 36
0
200
400
600
800
1000
1200
1400
Frequency
(cm
-1
)
Total
C
N
B
Γ M K Γ A L H A PDOS
Material C11 C33 C44 C66 C12 C13
Bulk
Modulus(B)
Young
modulus(E)
Shear
Modulus(G)
h-BC6N 1182.98 1298.11 438.90 537.20 108.58 20.33 440.00 1107.40 512.30
h-Diamond 1251.52 1367.74 483.00 579.40 92.61 20.00 450.74 1182.45 556.31
h-BC2N 1091.10 1146.23 399.50 498.70 93.60 2.97 391.90 1007.40 470.05
 High bond strength and lower atomic
masses leads to high phonon frequencies
and phonon group velocities
 Large number of optical phonons with
high frequencies contributes to the
nanoscale thermal conductivity
Phonon dispersion of Silicon
Phonon dispersion of BC6N

37. BC6N– Phonon meanfreepaths
8/7/2021 37
At L< 100 nm, Optical phonons
contributes to its overall k
At nanometer length scales L<100 nm,
optical phonons contributes much of its
thermal conductivity

38. References
1. Li, X., et al., Enhanced through-plane thermal conductivity in Polymer nanocomposites by constructing graphene-supported BN
nanotubes. Journal of Materials Chemistry C, 2020. 8(28): p. 9569-9575.
2. Liem, H. and H.S. Choy, Superior thermal conductivity of polymer nanocomposites by using graphene and boron nitride as
fillers. Solid State Communications, 2013. 163: p. 41-45.
3. Agarwal, S., M.M.K. Khan, and R.K. Gupta, Thermal conductivity of polymer nanocomposites made with carbon nanofibers.
Polymer Engineering & Science, 2008. 48(12): p. 2474-2481.
4. Sang, M., et al., Electronic and Thermal Properties of Graphene and Recent Advances in Graphene Based Electronics
Applications. Nanomaterials (Basel, Switzerland), 2019. 9(3): p. 374.
5. Fugallo, G., et al., Thermal Conductivity of Graphene and Graphite: Collective Excitations and Mean Free Paths. Nano Letters,
2014. 14(11): p. 6109-6114.
6. Pop, E., V. Varshney, and A.K. Roy, Thermal properties of graphene: Fundamentals and applications. MRS Bulletin, 2012. 37(12):
p. 1273-1281.
7. Muthaiah, R. and J. Garg, Strain tuned high thermal conductivity in boron phosphide at nanometer length scales – a first-
principles study. Physical Chemistry Chemical Physics, 2020.
8. Yuan, C., et al., Modulating the thermal conductivity in hexagonal boron nitride via controlled boron isotope concentration.
Communications Physics, 2019. 2(1): p. 43.
9. Li, S., et al., High thermal conductivity in cubic boron arsenide crystals. Science, 2018. 361(6402): p. 579-581.
10. Kang, J.S., et al., Experimental observation of high thermal conductivity in boron arsenide. Science, 2018. 361(6402): p. 575-
578.
11. Lindsay, L., D.A. Broido, and T.L. Reinecke, First-Principles Determination of Ultrahigh Thermal Conductivity of Boron Arsenide: A
Competitor for Diamond? Physical Review Letters, 2013. 111(2): p. 025901.
12. Martinez, L., et al., PACKMOL: a package for building initial configurations for molecular dynamics simulations. J Comput
Chem, 2009. 30(13): p. 2157-64.
8/7/2021 38

39. List of Publications
• Rajmohan Muthaiah and Jivtesh Garg. "Temperature effects in the thermal conductivity of aligned
amorphous polyethylene—A molecular dynamics study." Journal of Applied Physics 124.10 (2018):
105102.
• Rajmohan Muthaiah and Jivtesh Garg. "Strain tuned high thermal conductivity in boron phosphide at
nanometer length scales–a first-principles study." Physical Chemistry Chemical Physics 22.36 (2020):
20914-20921.
• Rajmohan Muthaiah, et al. "Thermal conductivity of hexagonal BC 2 P–a first-principles study." RSC
Advances 10.70 (2020): 42628-42632.
• Rajmohan Muthaiah and Jivtesh Garg. "Thermal conductivity of magnesium selenide (MgSe)–A first
principles study." Computational Materials Science 198 (2021): 110679.
• Rajmohan Muthaiah, Fatema Tarannum and Jivtesh Garg. "Strain tuned low thermal conductivity in
Indium Antimonide (InSb) through increase in anharmonic phonon scattering-A first-principles
study." Solid State Communications 334 (2021): 114378.
• Rajmohan Muthaiah and Jivtesh Garg. "Strain tuned thermal conductivity reduction in Indium
Arsenide (InAs)–A first-principles study." Computational Materials Science 196 (2021): 110531.
• Rajmohan Muthaiah and Jivtesh Garg, Thermal conductivity of magnesium telluride (MgTe) - A first
principles study. Solid State Communications 337 (2021): 114414.
• Fatema Tarannum, Rajmohan Muthaiah and Jivtesh Garg "Effect of Alignment on Enhancement of Thermal
Conductivity of Polyethylene–Graphene Nanocomposites and Comparison with Effective Medium
Theory." Nanomaterials 10.7 (2020): 1291.
8/7/2021 39

40. Acknowledgement
• Family members(Muthaiah Kamatchi, Easwari Muthaiah, Nagaraj Muthaiah, Bhuvaneshwari
Nagaraj, Jeyashree Venkateshkumar, Ivanshika Jeyaraj and generations of Kamatchi-Sarojini
and Surulivel-Subbulakshmi)
• Dr.Jivtesh Garg, Associate Professor, AME
• Doctoral Committee Members
• Professor Farrokh Mistree, AME
• School of Aerospace and Mechanical Engineering and GCoE
• Dr.Lucas Lindsay, Materials Scientist, Oak Ridge National Lab
• Dr.Tribhuwan Pandey, Postdoc, University of Antwerp, Belgium
• Dr.Carlos Polanco, Postdoc, Oak Ridge National Lab
• Dr.Vinit Sharma, Materials Scientist, Oak Ridge National Lab
• Friends and relatives
• Lab Members(Fatema Tarannum, Roshan Sameer Annam, Avinash Singh Nayal, Swapneel
Danayat)
• AME staff members(Bethany, Melissa, Martina, Ellen, Billy and Paula)
• Sri Sairam Institute of technology and former colleagues
• Dr.Dharmahinder Singh Chand and Dr.Bhoominathan, Mentor, Undergraduate Program
8/7/2021 40

41. THANKS
8/7/2021 41

42. Project 2C: Band diagram, Seebeck Coefficient and Electrical conductivity of
InAs with strain
8/7/2021 42
Figure S2: Band diagram of unstrained and 3% biaxial compressive strained InAs Figure S3: a) Electrical conductivity and b) Seebeck coefficient for unstrained and 3% biaxially
compressed InAs.
-0.20 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15
0
2
4
6
8
-0.20 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15
-600
-400
-200
0
200
400
600
800
Electrical
conductivity(1/(W
cm)
Chemical Potential m - Ef (Ry)
e = 0 %
e = -3 %
Seebeck
Coefficient
(V/K)
e = 0 %
e = -3 %
Chemical Potential m - Ef (Ry)