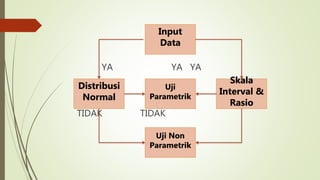
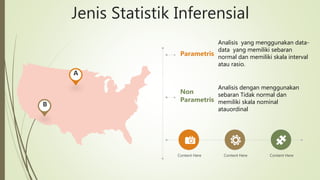
Statistik inferensial digunakan untuk menyimpulkan data sampel dan populasi. Terdapat dua jenis statistik inferensial yaitu parametrik yang menggunakan data normal dan nonparametrik untuk data tidak normal. SPSS menyediakan berbagai metode inferensial seperti uji-t, ANOVA, korelasi dan regresi.

1. Pengantar Statistik Infrensial
Nusrotus Sa’idah, M.Pd

2. Pengertian
Statistik yang digunakan untuk menyimpulkan atau
menggeneralisasikan data sampel dari bagian populasi
Untuk menentukan kebenaran data pengambilan
sampel dari populasi maka diperlukan nilai α (tingkat
signifikansi).

3. YA YA YA
TIDAK TIDAK

4. Jenis Statistik Inferensial
Analisis yang menggunakan data-
data yang memiliki sebaran
normal dan memiliki skala interval
atau rasio.
Parametris
Analisis dengan menggunakan
sebaran Tidak normal dan
memiliki skala nominal
atauordinal
Non
Parametris
Content Here Content Here Content Here
A
B

5. Karakteristik Statistik Inferensial
Distribusi
Data
Teknik
Pengambilan
sampling
Varians
Kelompok
Skala
Pengukuran
Content Here
You can simply impress your
audience and add a unique zing
and appeal to your Presentations.
Parametris : Interval dan Rasio
Non Parametris : nominal dan
ordinal
Parametris : Varians kelompok
Homogen
Nonparametris: Tdak homogeny
Jika Parametris penarikan sampel
random , Non Parametris sampel
tidak random
Untuk Parametris Berdistribusi
Normal , Non Parametris Tidak
berdistribusi Normal

6. STATISTIK PARAMETRIK
 Statistik parametrik: yaitu statistik yang digunakan untuk menguji hypotesis yang
variabelnya terukur.
 Contoh: “Berapa menit rata-rata Mahasiswa belajar dirumah?“
 Variabel waktu belajar dapat terukur dalam menit (ada standar)
 Contoh metode statistika parametrik: uji-z (1 atau 2 sampel), uji-t (1 atau 2 sampel), korelasi
pearson, Perancangan Percobaan (1 or 2-way ANOVA parametrik), dll.

7. STATISTIK NON PARAMETRIK
 Statistik Non parametrik adalah statistik yang digunakan untuk menguji hypotesis yang
variabelnya tidak memiliki kepastian (standar)
 Contoh: “Berapa besar kepuasan Mahasiswa terhadap pembelajaran Daring ?“
 Variabel kepuasan tidak memiliki standar pasti.
 Data statistic non parametris tidak mensyaratkan normal atau tidak. Statistika non-parametrik
biasanya digunakan untuk melakukan analisis pada data berjenis Nominal atau Ordinal. Data
berjenis Nominal dan Ordinal tidak menyebar normal. Contoh metode Statistika non-parametrik:
Binomial test, Chi-square test, Median test, Friedman Test, dll.

8.  Statistik Inferensial , pengujian hipotesis sangat penting dalam
menentukan tujuan dalam menjawab rumusan masalah. Hipotesis ini
selalalu didukung oleh fakta. Pengujian hipotesis (yang menggambarkan
karakteristik populasi) dengan menggunakan data sampel (yang
menggambarkan karakteristik sampel) pada dasarnya merupakan
pembuatan keputusan melalui proses inferensi yang memerlukan akurasi
peneliti dalam melakukan estimasi
 Proses Inferensi dapat dilakukan dengan estmasi nilai parameter populasi atau
membuat keputusan mengenai nilai parameter.
 Estimasi Nilai parameter tergantung pada representasi sampel yang diambil dari
populasi, peneliti harus mempunyai kriteria yang digunakan untuk membuat
keputusan terhadap hipotesis yang diuji berdasarkan sampel. Kriteria keputusan
yang ditetapkan oleh peneliti dalam istilah statistik disebut tingkat signifikansi
(significance level).

9. Tingkat signifikansi adalah tingkat probabilitas yang ditentukan
oleh peneliti untuk membuat keputusan menolak atau
mendukung hipotesis. Kriteria keputusan berdasarkan tingkat
signifikansi, misalnya 0,05 atau 0,01 menunjukkan bahwa
keputusan yang dibuat oleh peneliti untuk menolak atau
mendukung suatu hipotesis mempunyai probablilitas
kesalahan sebesar lima persen atau sepuluh persen.

10. a. Inferensi terhadap sebuah rata-rata populasi
Tujuan analisis ini untuk mengetahui apakah sampel yang kita teliti memiliki rata-rata mean atau menguji
apakah sampel mewakili populasi
· Sampel Besar
Dalam kasus dimana jumlah sampel yang diambil cukup besar atau varians populasi diketahui,
maka bisa dipakai rumus (uji) z.
· Sampel Kecil
Jika sampel kecil (<30) dan varians populasi tidak diketahui, metode parametrik yang digunakan
adalah uji t (student).
2.Berbagai Metode Parametrik

11. b. Inferensi terhadap dua rata-rata populasi
Dalam inferensi dua populasi, tujuan utama adalah ingin mengetahui apakah
ada perbedaan antara dua rata-rata populasi.
· Sampel Besar
Metode yang digunakan adalah z test yang dimodifikasi.
· Sampel Kecil
Metode yang digunakan adalah:
-> t test yang dimodifikasi : sampel bisa saling berhubungan (dependen)
maupun kedua sampel tidak ada hubungannya (independen).
-> F test (Uji F)
c. Inferensi terhadap lebih dari dua rata-rata populasi
Untuk lebih dari dua populasi, misal tiga jenis sampel, empat jenis sampel dan
seterusnya, dipakai analisis ANOVA, yang terdiri atas:
 ANOVA satu faktor
ANOVA dua faktor dengan replacement
ANOVA dua faktor tanpa replacement

12. d. Inferensi untuk mengetahui apakah ada hubungan
antara variabel
Inferensi ini bertujuan untuk mengetahui apakah ada
hubungan yang signifikan antara dua variabel. Beberapa
alat statistik untuk mengetahui hubungan antar
variabel:
Hubungan antar dua variabel, menggunakan korelasi
dan regresi sederhana.
Hubungan antara lebih dari dua variabel (tiga, empat,
dan seterusnya), menggunakan metode korelasi dan
regresi berganda.

13. 3. Statistik Inferensi dalam SPSS
SPSS menyediakan berbagai metode parametrik untuk melakukan inferensi terhadap
data statistik. Oleh karena luasnya cakupan parametrik, maka inferensi dengan
parametrik akan dibagi dalam beberapa menu pada SPSS, yaitu menu COMPARE
MEANS, GENERAL LINEAR MODEL (GLM), CORRELATE, dan REGRESSION.
 COMPARE MEANS
Pembahasan pada COMPARE MEANS meliputi:
 MEANS
Bagian ini membahas hal yang sama pada statistik deskriptif, dengan penyajian
subgrup dan ditambah dengan uji linearitas.
 UJI t
Bagian ini meliputi:
 Uji t satu sampel (ONE SAMPLE T-TEST)
 Uji t untuk dua sampel independen (INDEPENDENT SAMPLES T-TEST)
 Uji t untuk dua sampel berpasangan (PAIRED SAMPLES T-TEST)
 ONE WAY ANOVA
Jika uji t untuk dua sampel, maka ANOVA digunakan untuk menguji lebih dari dua
sampel.

14. Analisis Parametris dengan SPSS
SPSS menyediakan berbagai metode parametrik untuk melakukan inferensi terhadap data statistik. Oleh
karena luasnya cakupan parametrik, maka inferensi dengan parametrik akan dibagi dalam beberapa menu
pada SPSS, yaitu menu COMPARE MEANS, GENERAL LINEAR MODEL (GLM), CORRELATE, dan REGRESSION.
 COMPARE MEANS
Pembahasan pada COMPARE MEANS meliputi:
 MEANS
Bagian ini membahas hal yang sama pada statistik deskriptif, dengan penyajian subgrup dan ditambah
dengan uji linearitas.
 UJI t
Bagian ini meliputi:
 Uji t satu sampel (ONE SAMPLE T-TEST)
 Uji t untuk dua sampel independen (INDEPENDENT SAMPLES T-TEST)
 Uji t untuk dua sampel berpasangan (PAIRED SAMPLES T-TEST)
 ONE WAY ANOVA
Jika uji t untuk dua sampel, maka ANOVA digunakan untuk menguji lebih dari dua sampel.

15. GENERAL LINEAR MODEL
GLM merupakan kelanjutan dari ANOVA, dimana pada GLM dibahas satu
variabel dependen namun mempunyai satu atau lebih faktor.
CORRELATE
Membahas uji hubungan antara dua variabel.
REGRESSION
Membahas pembuatan model regresi untuk menggambarkan hubungan dua
variabel atau lebih.