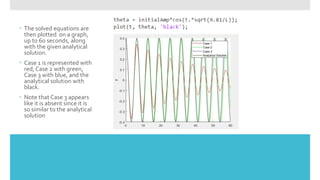
This document summarizes a program that models the motion of a pendulum. The program takes initial amplitude and length as inputs, uses differential equations to calculate the pendulum's position over time for different cases, and plots the solutions on a graph. It also exports the data to a text file in table format.

1. Pendulum Model

2.  The program initially asks for
a value for initial amplitude,
represented by variable
initialAmp and length of the
pendulum, represented by
the variable L
 Uses a while loop to check if
the L value and initialAmp
value are positive
 Checks if the assumption of
small angles is valid

3.  Next the program solves a
system of first order
differential equation for
the position at certain
times given the
length using the
ode45 function. It solves
one of these for each
case. It then plots these
on a graph.

4.  The program uses functions to
solve the system of equations
and stores the values in an array
 In this program the mass,
damping effect and gravity are
inside the equation as the
numbers given for them instead
of as variables to save lines of
code.

5.  The solved equations are
then plotted on a graph,
up to 60 seconds, along
with the given analytical
solution.
 Case 1 is represented with
red, Case 2 with green,
Case 3 with blue, and the
analytical solution with
black.
 Note that Case 3 appears
like it is absent since it is
so similar to the analytical
solution

6.  The program creates a
txt file named
"PendulumSolution.txt"
in write mode and adds
the data for each
solution into a table
 The first fprint
statement prints the
titles of each column
into the .txt file
 The for loop prints the
time and solution for
each of the cases
 Added "|" and "_"
symbols to create a
table

7.  The data printed by the
previous set of code is
outputted into the .txt
file as shown
 Formatting the table
gave us some challenges
since not every value
was the same number of
digits