- The document discusses the partial fraction theorem and convolution theorem for evaluating integrals involving rational functions. - It provides examples of using partial fraction decomposition to split rational functions into sums of simpler fractional components. Convolutions of the inverse Laplace transforms of the components are used to evaluate the original integral. - Problems are presented and solved step-by-step using these techniques, like decomposing a rational function into sums of terms with distinct denominators and using properties of inverse Laplace transforms.

1. Partial Fraction Theorem
• Lecture -16
Yaindrila Barua
Lecturer, GED,
DIU

2. 𝓛−𝟏 𝒇 𝒔 = 𝑭(𝒕) 𝓛−𝟏 𝒈 𝒔 = 𝑮(𝒕)
ℒ−1
𝑓 𝑠 𝑔 𝑠 =? ? ?
=
0
𝑡
𝐹 𝑢 𝐺 𝑡 − 𝑢 𝑑𝑢
= 𝐹 ∗ 𝐺
Convolution Theorem

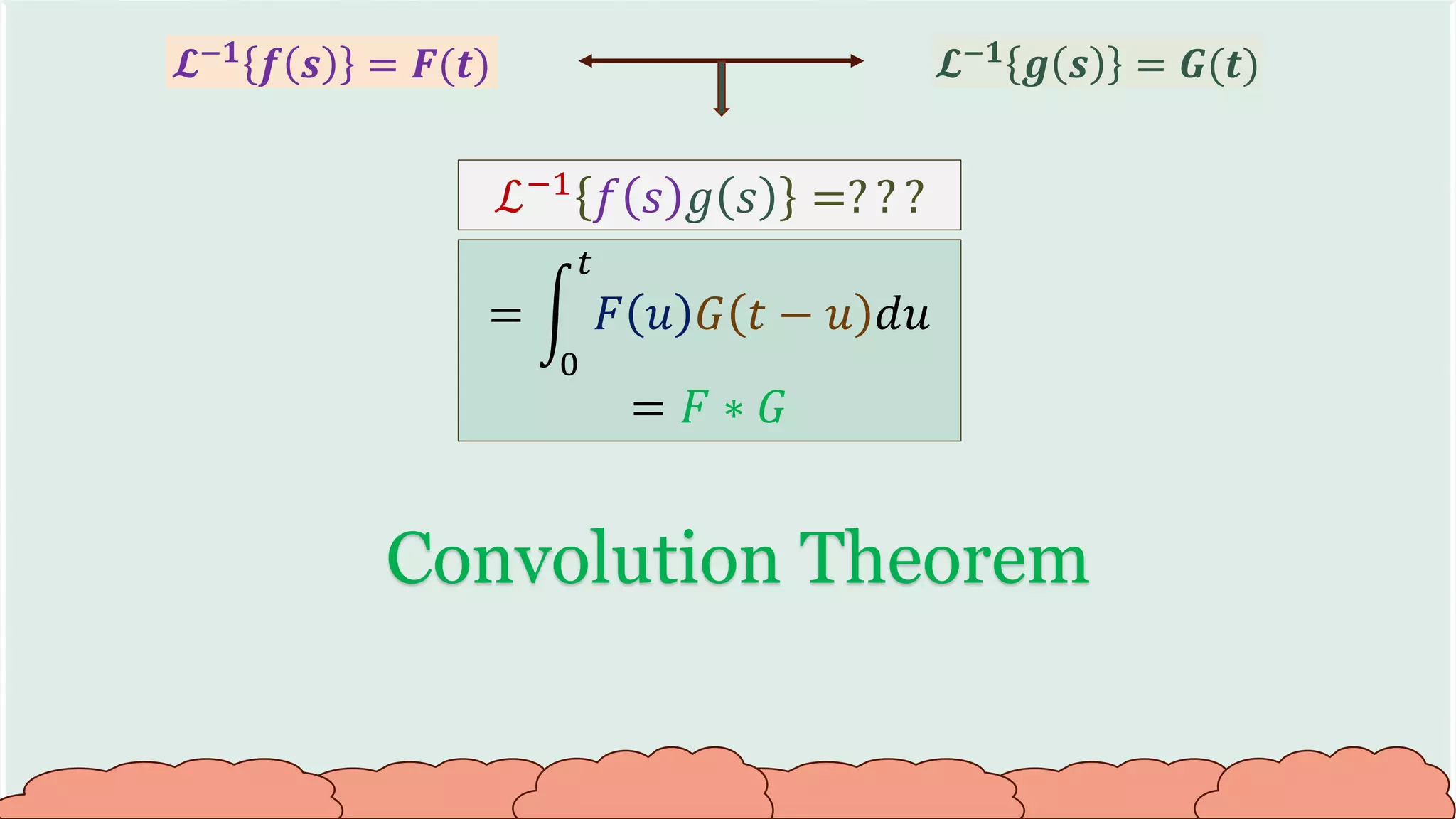
3. 𝓛−𝟏 𝒇 𝒔 = 𝑭(𝒕) 𝓛−𝟏 𝒈 𝒔 = 𝑮(𝒕)
𝓛−𝟏
𝟑
𝒔 − 𝟒
= 𝟑𝒆 𝟒𝒕 𝓛−𝟏
𝟒
𝒔 + 𝟗
= 𝟒𝒆−𝟗𝒕
ℒ−1
12
(𝑠 − 4)(𝑠 + 9)
=? ? ?
=
0
𝑡
𝐹 𝑢 𝐺 𝑡 − 𝑢 𝑑𝑢
𝐹(𝑡) 𝐺(𝑡)
=
0
𝑡
12𝑒4𝑢
𝑒−9𝑡+9𝑢
𝑑𝑢
= 12𝑒−9𝑡
0
𝑡
𝑒13𝑢
𝑑𝑢 = 12𝑒−9𝑡
[
𝑒13𝑢
13
]0
𝑡
=
12
13
𝑒−9𝑡
[𝑒13𝑡
− 1]

4. Convolution Theorem
8/8/2020
4
Problems: Evaluate the following using Convolution theorem

5. Problems on Convolution Theorem
Solution (a):
8/8/2020 5
We can write,
1
(s -1)(s -2)
=
1
(s -1)
×
1
(s -2)
Let f (s)=
1
(s -1)
and g(s)=
1
(s -2)

6. Problems on Convolution Theorem
8/8/2020
6
= eu
0
t
ò e2(t-u)
du = eu
0
t
ò e2t
e-2u
du
= e2t
e-u
0
t
ò du = e2t
-e-u
é
ë
ù
û0
t
= -e2t
e-t
-e0
é
ë
ù
û
= -e2t
e-t
-1é
ë
ù
û = -e2t-t
+e2t
= e2t
-et
(Ans)

7. Partial Fraction Method
Problems: Evaluate the following using partial fraction method
8/8/2020 7

8. Partial Fraction Method
Solution (a):
8/8/2020
8
We can write,
2s2
-4
(s +1)(s -2)(s -3)
º
A
(s +1)
+
B
(s -2)
+
C
(s -3)
××××××(1)
2s2
-4= A(s-2)(s-3)+B(s+1)(s-3)+C(s+1)(s-2)××××××××(2)
Now, putting s = -1, 2, and 3 inequation(2), we get
2×1-4= A(-1-2)(-1-3)+0+0
Þ12A= -2 A=
-1
6
2×22
-4=0+B(2+1)(2-3)+0 B = -
4
3

9. Partial Fraction Method
Again,
8/8/2020
9
2×32
-4=0+0+C(3+1)(3-2) C =
7
2
Now, putting the values of A,B,and C inequation(1), we get
2s2
-4
(s +1)(s -2)(s -3)
=
-1/6
(s +1)
+
-4/3
(s -2)
+
7/2
(s -3)
=
-1
6
e-1t
+
-4
3
e2t
+
7
2
e3t
(Ans)

10. Partial Fraction Method
Solution (b):
8/8/2020
10
We can write,
3s +1
(s -1)(s2
+1)
=
A
s -1
+
Bs +c
s2
+1
×××××××××(1)
3s+1= A(s2
+1)+(Bs+C)(s-1)××××××××(2)
Now, putting s =1 inequation(2), we get
3×1+1= A(12
+1)+0
Þ2A=4 A=2
Now, equating the coefficient of s2
and constants form(2)
0= A+B ÞB = -A, therefore B = -2

11. Partial Fraction Method
8/8/2020
11
Again for constant, 1= A-C
1=2-C C =1
Now, putting the values of A,B,andC inequation(1), we get
3s +1
(s -1)(s2
+1)
=
2
s -1
+
-2s +1
s2
+1
=2et
-2cost +sint (Ans)
=
2
s -1
-2
s
s2
+12
+
1
s2
+12

12. Partial Fraction Method
Solution (b):
8/8/2020
12
We can write,
5s2
-15s-11
(s+1)(s-2)3
º
A
s+1
+
B
(s-2)
+
C
(s-2)2
+
D
(s-2)3
×××××××××(1)
5s2
-15s-11º A(s-2)3
+B(s+1)(s-2)2
+C(s+1)(s-2)+D(s+1)××××××××(2)
Now, putting s = -1 inequation(2), we get
Now, equating the coefficient of s3
,s2
,s and constants form(2)
Do by yourself
Do by yourself