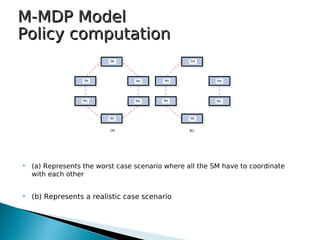
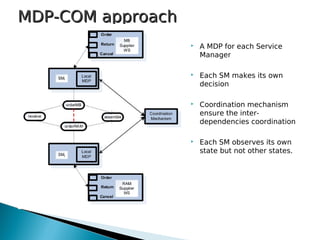
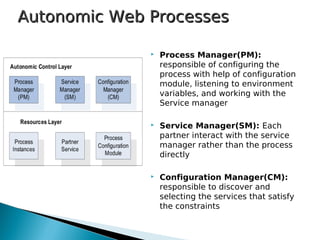
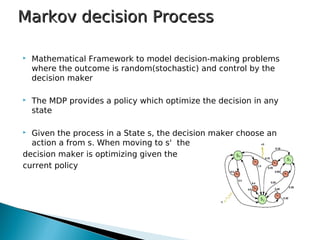
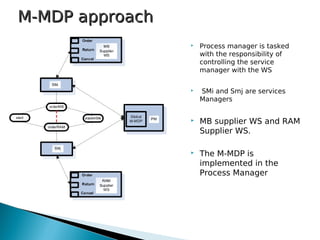
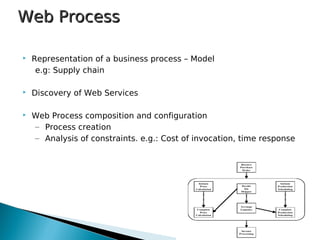
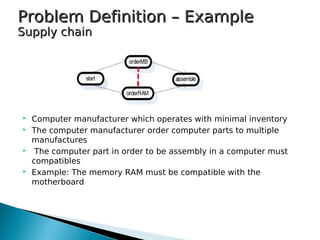
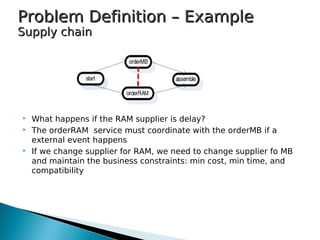
1) The document presents frameworks for optimal adaptation in autonomic web processes that have inter-service dependencies. It describes two approaches: M-MDP which uses a centralized Markov decision process and MDP-COM which uses a decentralized approach with local Markov decision processes and a coordination mechanism. 2) The supply chain example involves ordering computer parts from suppliers, with the goal of minimizing costs and response times while maintaining compatibility between parts. External events like delivery delays require adaptation. 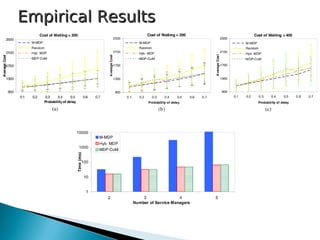3) The approaches were tested on a supply chain process implemented in METEOR-S, comparing performance under different horizons, event probabilities, and numbers of service managers. A hybrid model combining aspects of both approaches was also explored.

1. Presented by
Manuel Correa
Optimal Adaptation in AutonomicOptimal Adaptation in Autonomic
Web Processes with Inter-ServiceWeb Processes with Inter-Service
DependenciesDependencies
By Kunal Verma, Prashant Doshi, Karthik Gomadam, Amith SethBy Kunal Verma, Prashant Doshi, Karthik Gomadam, Amith Seth
20062006

2.  Web Process = WS composition = business process (BPEL)
 Autonomic Web Process (AWP) = Framework to WP Self-
Adaptation, Self-optimality and self-healing
 Inter-service dependencies = WS dependencies within a Web
process
 Optimal adaptation = Adaptation to exogenous events in the web
process (exogenous events = external events)
IntroductionIntroduction
Optimal Adaptation in Autonomic Web ProcessesOptimal Adaptation in Autonomic Web Processes
with Inter-Service Dependencieswith Inter-Service Dependencies

3.  Representation of a business process – Model
e.g: Supply chain
 Discovery of Web Services
 Web Process composition and configuration
– Process creation
– Analysis of constraints. e.g.: Cost of invocation, time response
Web ProcessWeb Process

4.  Processes must adapt to any external event in a dynamic
environment
 This adaptation must be optimal: Time, cost and other business
constraints
 Adaptation is hard to accomplish because the service inter
dependencies
Problem DefinitionProblem Definition

5.  Computer manufacturer which operates with minimal inventory
 The computer manufacturer order computer parts to multiple
manufactures
 The computer part in order to be assembly in a computer must
compatibles
 Example: The memory RAM must be compatible with the
motherboard
Problem Definition – ExampleProblem Definition – Example
Supply chainSupply chain

6.  What happens if the RAM supplier is delay?
 The orderRAM service must coordinate with the orderMB if a
external event happens
 If we change supplier for RAM, we need to change supplier fo MB
and maintain the business constraints: min cost, min time, and
compatibility
Problem Definition – ExampleProblem Definition – Example
Supply chainSupply chain

7. Quantitative constraints
– Invocation time <10
– Invocation Cost
– Cost of the supplier<2000
In order to discover services
with this constraints. The ILP
method was applied.
ILP: Integer Linear programming
Problem Definition – ExampleProblem Definition – Example
Supply chain – Discovery servicesSupply chain – Discovery services
Logical constraints
– Computer part's
Compatibility
For each set that meet the
quantitative constraints, we
need to validate if the
services are compatible.
Using Domain knowledge and
the SWRL technique
SWRL: Semantic Web Rule
Language

8.  Self-Configuration: AWP must be able to configure itself
automatically or semi-automatically
 Self-healing: AWP must be able to adapt to external and internal
failures
 Self-Optimization: AWP must achieve their goals in a cost-
effective and time-effective manner
Autonomic Web ProcessesAutonomic Web Processes

9.  Process Manager(PM):
responsible of configuring the
process with help of configuration
module, listening to environment
variables, and working with the
Service manager
 Service Manager(SM): Each
partner interact with the service
manager rather than the process
directly
 Configuration Manager(CM):
responsible to discover and
selecting the services that satisfy
the constraints
Autonomic Web ProcessesAutonomic Web Processes

10.  Centralized Approach: M-MDP ( Multi-Agent Markov Decision
process)
 DecentralizedApproach: MDP-COM ( Markov decision Model –
Coordination Mechanism)
Optimal AdaptationOptimal Adaptation

11.  Mathematical Framework to model decision-making problems
where the outcome is random(stochastic) and control by the
decision maker
 The MDP provides a policy which optimize the decision in any
state
 Given the process in a State s, the decision maker choose an
action a from s. When moving to s' the
decision maker is optimizing given the
current policy
Markov decision ProcessMarkov decision Process

12.  MDP is a tuple where M = (S, A, T, C, H)
• S= Set of states
• A= set of all possible actions
• T =Transition function T: SxA --> Prob(S) which specifies the probability
of the states given a current state and actions
• C: SxA --> |R Cost function which specifies the cost in given state and
action
• H: period the consideration where the solution is optimal, call also the
horizon 0<H<ꝏ
Markov decision ProcessMarkov decision Process
Formal definitionFormal definition

13.  Process manager is tasked
with the responsibility of
controlling the service
manager with the WS
 SMi and Smj are services
Managers
 MB supplier WS and RAM
Supplier WS.
 The M-MDP is
implemented in the
Process Manager
M-MDP approachM-MDP approach

14.  M-MDP generalize MDP by
considering the joint of actions of
different agents.
 Model
PM=(S, PA, T, C, OC)
M-MDP ModelM-MDP Model

PM = Process manager

S = Global states of the web
process

PA: A= set of joint of all the
services manager's actions

T: Markovian Transition
function.

C: Global cost of invoking the
WS

OC: Optimal criterion. Horizon.

15.  S= Set of states
S= Si x Sj. Factored states of the
service managers
s = (si, sj);
M-MDP Model – detailsM-MDP Model – details
PM = (S, PA, T, C, OC)PM = (S, PA, T, C, OC)

PA: S-->P(A)
A =Ai x Aj Factored actions in the
services managers
P(A): Set of permitted joint
actions in a State s
P(A) = PAi(Ai) x Paj(Aj)
PAi(Ai) : set of permitted action of
Service Manager i
Paj(Aj): set of permitted actions of
Service Manager j

16.  C=SxA -->|R
Cost function: Cost of invocation + cost of
waiting for delayed order + cost of
changing supplier
 OC: optimal criterion.
Horizon= Expected cost over finite steps.
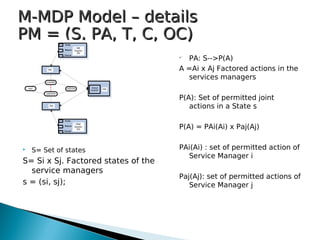
M-MDP Model – detailsM-MDP Model – details
PM = (S, PA, T, C, OC)PM = (S, PA, T, C, OC)

T = SxAxS --> [0,1]. Markovian
transition function
Captures the global effect of
jointly invoking WS by SM
T(s'|s,a) = T[(s'i, s'j) | (si, sj),(ai, aj)]
...
T(s'|s,a)= Ti[s'i | (si, ai)] * Tj[s'j, (sj,aj)]
Ti and Tj individual transition functions
This is possible because each service
manager's next state is influenced
only by its own action and its current
state.

17. M-MDP Model – detailsM-MDP Model – details
Example: Supply chainExample: Supply chain
 Global state Process:
This means the Service Manager SMi has placed an order but
not yet received it nor has any indication of delay. SMi has
not changed supplier
SMj has placed an order that has been delayed. SMj has not
change supplier
O: Place order
D: Delayed
CS: Change Supplier
R: Received
 Possible actions
Ai= Aj = {Order(O), Wait(W),
ChangeSupplier(CS) }

18. M-MDP Model – detailsM-MDP Model – details
Example: Supply chainExample: Supply chain
Table; Partial cost in PM

19. M-MDP Model – detailsM-MDP Model – details
Example: Supply chainExample: Supply chain
Graph with extended function. Modeling the external events
T=Si x Ai x Ei x Si.
Ei = {delayed, received, None)

20. M-MDP ModelM-MDP Model
Global Policy computationGlobal Policy computation
 Global policy: optimal action that must performed by each service
manager given a global state in Process Manager (PM)
 In order to compute the global policy, each global state is associated with a
value that represents the long term expected cost in that state
 An optimal global policy is guarantee.

21. M-MDP ModelM-MDP Model
Policy computationPolicy computation
 (a) Represents the worst case scenario where all the SM have to coordinate
with each other
 (b) Represents a realistic case scenario

22.  A MDP for each Service
Manager
 Each SM makes its own
decision
 Coordination mechanism
ensure the inter-
dependencies coordination
 Each SM observes its own
state but not other states.
MDP-COM approachMDP-COM approach

23.  Model
SMi =(Si, PAi, Ti, Ci, OCi)
MDP-COM ModelMDP-COM Model

SMi = Service Manager ith

Si = Local states of the SMi

Pai: Si -->P(Ai). Local
permissible actions by state

Ti: SixAixSi -->[0,1} Markovian
Transition function.

C: Si x Ai -->R Local cost of
invoking the WS

OC: Optimal criterion. Horizon.

24. MDP-COM Model – detailsMDP-COM Model – details
Example: Supply chainExample: Supply chain
 Local state Process:
O: Place order
D: Delayed
CS: Change Supplier
R: Received
 Possible actions
Ai= Aj = {Order(O), Wait(W),
ChangeSupplier(CS) }

25. MDP-COM Model – detailsMDP-COM Model – details
Coordination processCoordination process
 Since the optimal decision to respond to exogenous events is compute by
each SM. A coordination mechanism must be implement to preserve the
compatibility constraints
 A SMi must communicate to the others Service Manager its intent to
perform an action to respond to an event. ( Game Theory)
 The coordination mechanism is a Finite State machine. Two states:
Uncoordinate and Coordinate.
 Supply chain: when a SM for RAM
change Supplier, the orderMB
must follow this action
and change supplier

26. MDP-COM ModelMDP-COM Model
Local Policy computationLocal Policy computation
 Each state is associated with coordination states.
 Each Service Manager does not take into account the other states, actions
and costs of others Service Manager
 The model MDP-COM calculate policies locally and then coordinate with
other Service Managers to make the decision in the process
 Supply chain: If orderRAM change supplier then it coordinates with
orderMB to change supplier as well. Even though this is not the most
optimal solution

27. Empirical ResultsEmpirical Results
 This two methods were tested in METEOR-S framework. BPEL4WS was
used to implemented the Web process with WSDL-S
 First experiment M-MDP was tested with different horizons
 Second Experiment: Probability of events to occur. Such as delay in order.
And comparing the model with random choice of actions
 Third experiment: Number of service manager and time respond
 The test included a Hybrid model. With a MDP-COM giving the process
manager the ability to take some actions over the Service Manager.
e.g. if orderMB change supplier then the process Manager decides if the
process is better off changing supplier or taking another action.

28. Empirical ResultsEmpirical Results

29. ConclusionsConclusions
 Web processes are increasing and the study of optimal adaptability with
service inter dependencies is very important
 The M-MDP method does no t scale well with multiple Service Manager
 M-MDP computes optimal solutions because it has the whole picture of t he
process
 MDP-COM scales well. But it does not offer an optimal solution all the times
 Future work: An hybrid model that takes advantages of both models

30. Questions?
Optimal Adaptation in AutonomicOptimal Adaptation in Autonomic
WebWeb ProcessesProcesses with Inter-Servicewith Inter-Service
DependenciesDependencies