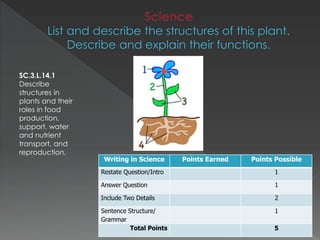
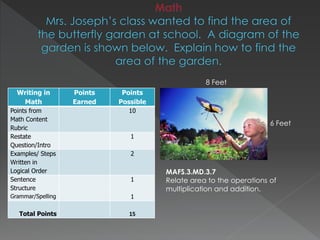
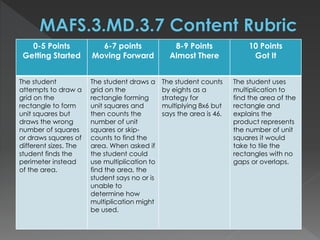
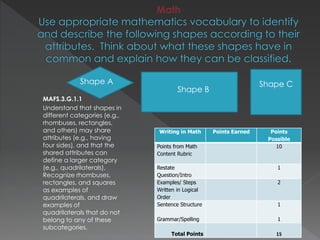
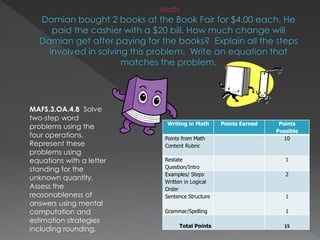
The document contains standards and learning targets for 3rd grade science and math. It includes standards about properties of matter, characteristics of plants, measurement of time and length, and fractions. It also provides examples of student work and rubrics to assess understanding of area, geometry, time telling, and multi-step word problems.

2. SC.3.E.5.5
Investigate that
the number of
stars that can be
seen through
telescopes is
dramatically
greater than
those seen by the
unaided eye.
Writing in Science Points Earned Points Possible
Restate Question/Intro 1
Answer Question 1
Include Two Details 2
Sentence Structure/
Grammar
1
Total Points 5

3. SC.3.P.11.2 -
Investigate,
observe, and
explain that heat
is produced
when one object
rubs against
another, such as
rubbing one's
hands together.
Writing in Science Points Earned Points Possible
Restate Question/Intro 1
Answer Question 1
Include Two Details 2
Sentence Structure/
Grammar
1
Total Points 5

4. Writing in Science Points Earned Points Possible
Restate Question/Intro 1
Answer Question 1
Include Two Details 2
Sentence Structure/
Grammar
1
Total Points 5
SC.3.P.9.1
Describe the
changes water
undergoes when
it changes state
through heating
and cooling by
using familiar
scientific terms
such as melting,
freezing, boiling,
evaporation, and
condensation.

5. Writing in Science Points Earned Points Possible
Restate Question/Intro 1
Answer Question 1
Include Two Details 2
Sentence Structure/
Grammar
1
Total Points 5
SC.3.P.10.4
Demonstrate
that light can
be reflected,
refracted,
and
absorbed.

6. SC.3.L.14.1
Describe
structures in
plants and their
roles in food
production,
support, water
and nutrient
transport, and
reproduction.
Writing in Science Points Earned Points Possible
Restate Question/Intro 1
Answer Question 1
Include Two Details 2
Sentence Structure/
Grammar
1
Total Points 5

7. 8 Feet
6 Feet
Writing in
Math
Points
Earned
Points
Possible
Points from
Math Content
Rubric
10
Restate
Question/Intro
1
Examples/ Steps
Written in
Logical Order
2
Sentence
Structure
Grammar/Spelling
1
1
Total Points 15
MAFS.3.MD.3.7
Relate area to the operations of
multiplication and addition.

8. 0-5 Points
Getting Started
6-7 points
Moving Forward
8-9 Points
Almost There
10 Points
Got It
The student
attempts to draw a
grid on the
rectangle to form
unit squares but
draws the wrong
number of squares
or draws squares of
different sizes. The
student finds the
perimeter instead
of the area.
The student draws a
grid on the
rectangle forming
unit squares and
then counts the
number of unit
squares or skip-
counts to find the
area. When asked if
the student could
use multiplication to
find the area, the
student says no or is
unable to
determine how
multiplication might
be used.
The student counts
by eights as a
strategy for
multiplying 8x6 but
says the area is 46.
The student uses
multiplication to
find the area of the
rectangle and
explains the
product represents
the number of unit
squares it would
take to tile the
rectangles with no
gaps or overlaps.

9. MAFS.3.G.1.1
Understand that shapes in
different categories (e.g.,
rhombuses, rectangles,
and others) may share
attributes (e.g., having
four sides), and that the
shared attributes can
define a larger category
(e.g., quadrilaterals).
Recognize rhombuses,
rectangles, and squares
as examples of
quadrilaterals, and draw
examples of
quadrilaterals that do not
belong to any of these
subcategories.
Shape A
Shape B
Shape C
Writing in Math Points Earned Points
Possible
Points from Math
Content Rubric
10
Restate
Question/Intro
1
Examples/ Steps
Written in Logical
Order
2
Sentence Structure
Grammar/Spelling
1
1
Total Points 15

10. 0-5 Points
Getting Started
6-7 points
Moving Forward
8-9 Points
Almost There
10 Points
Got It
The language used to
describe the shapes is
general and not
mathematically
accurate. The student
says, “they all have
sides,” “they all are
shapes,” or “they all
have corners.”
The student describes
specific shared attributes
using appropriate
mathematical
vocabulary, but is
unable to determine any
larger category to which
the shapes belong (i.e.,
quadrilaterals, polygons,
two-dimensional figures).
The student is unable to
classify all the shapes as
quadrilaterals even after
prompting with non-
examples. The student
can only describe the
shapes as two-
dimensional or as
polygons and even after
prompting does not
know the term
“quadrilateral” to
describe these three
shapes. The student
correctly names each
shape, tells what the
shapes have in common
(four sides, four vertices)
but does not know the
term quadrilateral,
which can be used to
describe all three
shapes.
The student correctly
names each shape,
describes specific shared
attributes using
appropriate
mathematical
vocabulary, and
describes all three
shapes as quadrilaterals,
with little to no
prompting.

11. Writing in Math Points Earned Points
Possible
Points from Math
Content Rubric
10
Restate
Question/Intro
1
Examples/ Steps
Written in Logical
Order
2
Sentence Structure
Grammar/Spelling
1
1
Total Points 15
MAFS.3.MD.1.1 Tell and write time to the
nearest minute and measure time intervals
in minutes. Solve word problems involving
addition and subtraction of time intervals
in minutes, e.g., by representing the
problem on a number line diagram.

12. 0-5 Points
Getting Started
6-7 points
Moving Forward
8-9 Points
Almost There
10 Points
Got It
The student
attempts to add
the elapsed
minutes to the
finish time given.
The student has an
effective strategy
for solving the
problem, and
attempts to count
back to find the
starting time but
makes significant
errors and gets lost
in his or her
strategy.
The student makes
a computational
error such as
subtracting 38
from 51 and
getting 23 instead
of 13. The student
says that Kai
started running at
9:13 a.m. instead
of 10:13 a.m.
The student
correctly subtracts
38 minutes from 51
minutes, getting a
final answer of
10:13 a.m.

13. MAFS.3.NF.1.3
Explain
equivalence of
fractions in special
cases, and
compare fractions
by reasoning
about their size.
Cake
A
Cake
B
Writing in Math Points Earned Points
Possible
Points from Math
Content Rubric
10
Restate
Question/Intro
1
Examples/ Steps
Written in Logical
Order
2
Sentence Structure
Grammar/Spelling
1
1
Total Points 15

14. 0-5 Points
Getting Started
6-7 points
Moving Forward
8-9 Points
Almost There
10 Points
Got It
The student says
Amanda ate three
pieces and Tanya
ate only one piece
so Amanda ate
more. The student
says that ¾ of cake
A is greater than ¼ of
cake B since ¾ is
greater than ¼ .
The student partitions
the two cakes into
fourths, shades three
of the fourths for
cake A and one of
the fourths for cake B,
but still concludes
that ¾ is greater
than ¼ .
The student partitions
the two cakes into
fourths, shades three of
the fourths for cake A
and one of the fourths
for cake B, and
concludes that ¼ of
cake A is greater than
¾ of cake B. But, the
student is unable to
explain that in order to
compare two fractions,
you have to know
something about the
wholes to which the
fractions refer.
The student may partition
the two cakes into fourths,
shade three of the fourths
for cake A and one of the
fourths for cake B, and
conclude that ¼ of cake A
is greater than ¾ of cake B.
Whether the student
actually partitions the
cakes or not, the student
explains that, since cake A
is much smaller than cake
B, that ¾ of cake A is less
than ¼ of cake B. The
student is able to conclude
that in order to compare
two fractions, he or she
must know something
about the whole(s) to
which the fractions refer.

15. MAFS.3.OA.4.8 Solve
two-step word
problems using the
four operations.
Represent these
problems using
equations with a letter
standing for the
unknown quantity.
Assess the
reasonableness of
answers using mental
computation and
estimation strategies
including rounding.
Writing in Math Points Earned Points
Possible
Points from Math
Content Rubric
10
Restate
Question/Intro
1
Examples/ Steps
Written in Logical
Order
2
Sentence Structure
Grammar/Spelling
1
1
Total Points 15

16. 0-5 Points
Getting Started
6-7 points
Moving Forward
8-9 Points
Almost There
10 Points
Got It
The student subtracts
$4.00 from $20.00
and says that the
books cost $16 or
that Damian will
receive $16 in
change. The student
multiplies $4 by 2 and
says that the books
cost $8 but fails to
subtract this from $20.
The student uses the
numbers presented in
the problem and
writes an equation,
but the equation
does not match the
word problem (e.g.,
the student writes (4 x
2) – 20 = 12).
The student correctly
solves the problem,
getting $12 as the
solution, and writes
an appropriate
equation (i.e., 20 – (4
x 2) = 12 or 4 x 2 = 8
and 20 – 8 = 12) but
when asked how he
or she knows that the
answer should be less
than 20, the student is
unable to explain his
or her reasoning.
The student correctly
solves the problem,
getting $12 as the
solution, and writes
an appropriate
equation (e.g., 20 –
(4 x 2) = 12 or 4 x 2 = 8
and 20 – 8 = 12).
When asked how he
or she knows the
answer should be less
than 20, the student is
able to clearly
explain that if you
pay with $20, you
must get less back as
change.