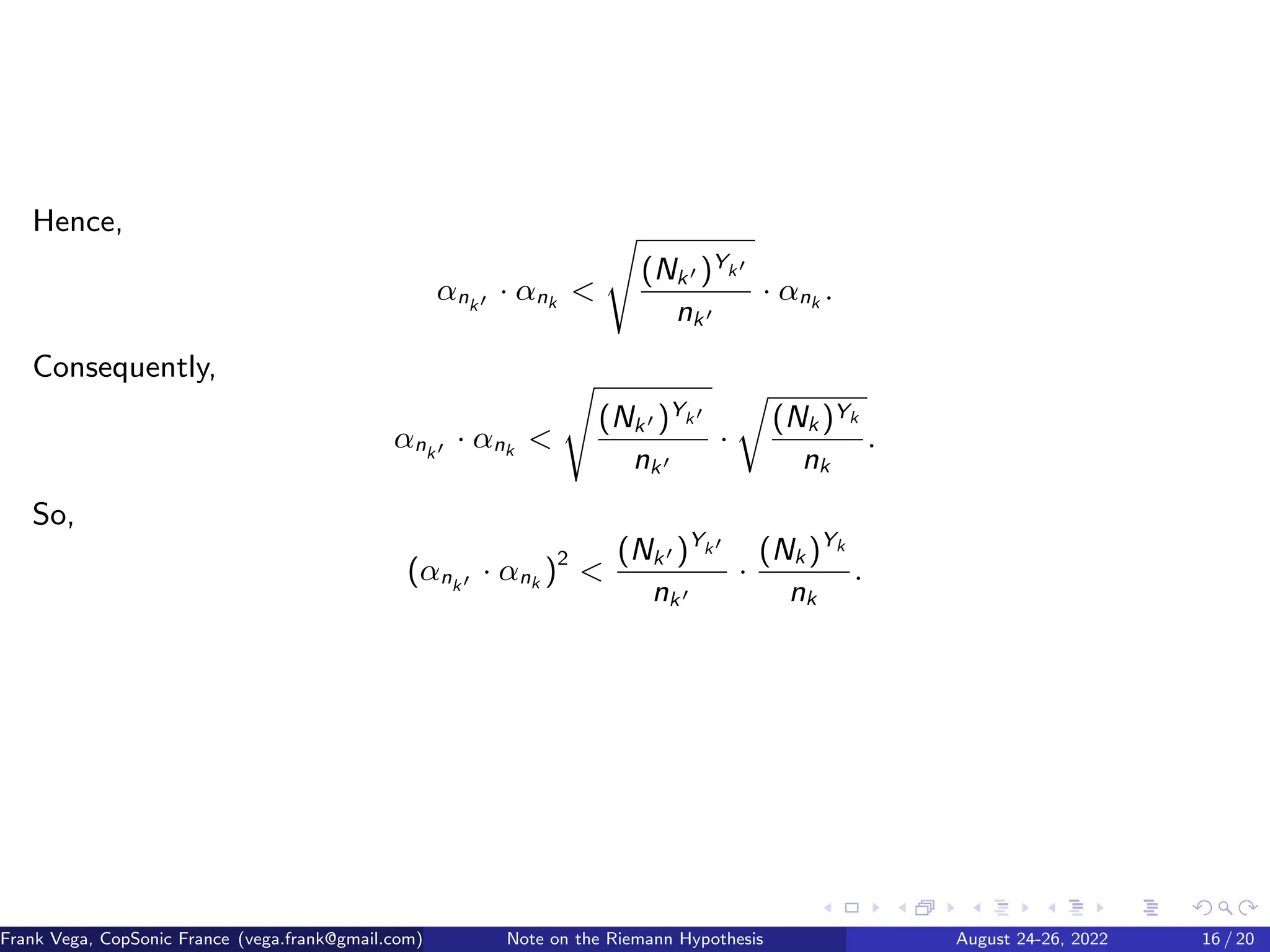
Frank Vega presents a proof of the Riemann Hypothesis, asserting that it holds true according to Robin's criterion, which relates properties of a function defined by the sum-of-divisors. The document discusses the significance of superabundant and colossally abundant numbers in relation to the hypothesis. This finding could lead to advancements in various fields of mathematics, emphasizing the hypothesis's importance as one of the Millennium Prize Problems.