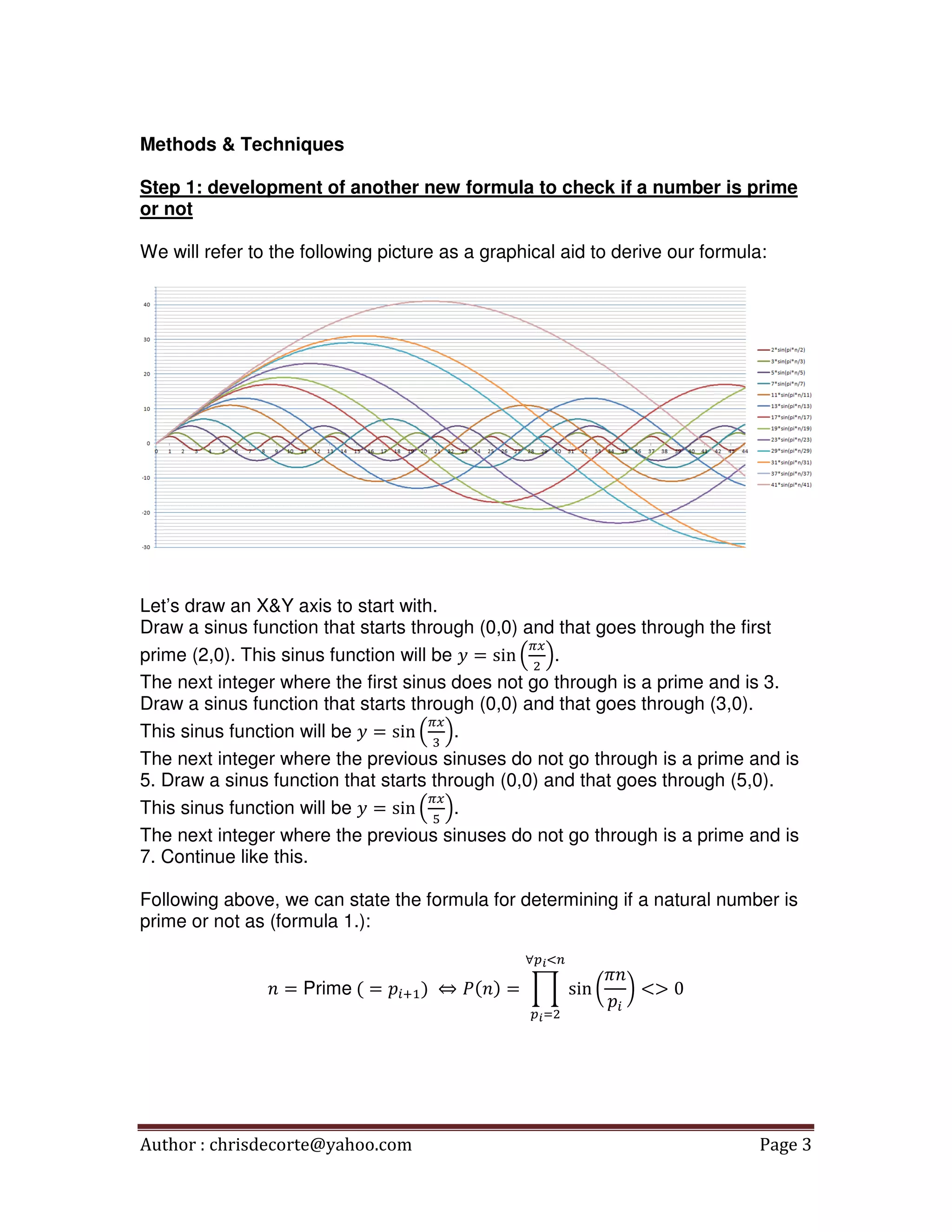
This document derives a new formula for determining if a number is prime and uses it to discuss open problems like the Goldbach conjecture and Polignac conjecture. The formula represents primes as integers where sinusoidal functions starting at each prime number do not intersect. The author argues this formula can prove: 1) Every even number is the sum of two primes, proving the Goldbach conjecture. 2) There are infinitely many prime number pairs with any given even difference, proving the Polignac conjecture. The author believes the formula is sufficiently powerful to prove existing prime number conjectures using basic trigonometric formulas and interpretations.

1. Author : chrisdecorte@yahoo.com Page 1
Yet another Prime formula and prove
of the related open problems

2. Author : chrisdecorte@yahoo.com Page 2
Abstract
In this document, we derive again a new formula to calculate prime numbers and
use it to discuss open problems like Goldbach and Polignac or Twin prime
conjectures. The derived formula is an interesting variant of my previous one.
Key-words
Zhang Yitang; Goldbach conjecture; twin prime conjecture; Polignac.
Introduction
The following document originated during our study of primes.
We tried to create a schematic representation of the mechanism that lead to the
creation of primes. Following, we tried to mathematically describe this graphical
representation. It resulted in a first new formula to calculate if a number is prime
or not. We explained about this formula in our previous document [1].
Shortly afterwards, we derived another prime formula that might be even more
powerful.
In the meantime, Zhang Yitang had come up with his prove with regard to prime
gaps. So, we will briefly reflect on this as well.

3. Author : chrisdecorte@yahoo.com Page 3
Methods & Techniques
Step 1: development of another new formula to check if a number is prime
or not
We will refer to the following picture as a graphical aid to derive our formula:
Let’s draw an X&Y axis to start with.
Draw a sinus function that starts through (0,0) and that goes through the first
prime (2,0). This sinus function will be ‫ݕ‬ = sin ቀ
గ௫
ଶ
ቁ.
The next integer where the first sinus does not go through is a prime and is 3.
Draw a sinus function that starts through (0,0) and that goes through (3,0).
This sinus function will be ‫ݕ‬ = sin ቀ
గ௫
ଷ
ቁ.
The next integer where the previous sinuses do not go through is a prime and is
5. Draw a sinus function that starts through (0,0) and that goes through (5,0).
This sinus function will be ‫ݕ‬ = sin ቀ
గ௫
ହ
ቁ.
The next integer where the previous sinuses do not go through is a prime and is
7. Continue like this.
Following above, we can state the formula for determining if a natural number is
prime or not as (formula 1.):
݊ = Prime ( = ‫݌‬௜ାଵሻ ⇔ ܲ(݊ሻ = ෑ sin ൬
ߨ݊
‫݌‬௜
൰ <> 0
∀௣೔ழ௡
௣೔ୀଶ

4. Author : chrisdecorte@yahoo.com Page 4
Step 2: splitting an even number into the sum of 2 primes
Goldbach’s conjecture states that every even number can be written as the sum
of two primes.
We can agree on following convention:
2n every even number
q the smaller prime number greater than 2 (and q≤p) (so q starts from 3)
p the larger prime number smaller than 2n-2
With: 2n=p+q
So for 2n, p and q, we will be able to write:
ܲ(2݊ሻ = ෑ sin ൬
ߨ2݊
‫݌‬௜
൰ = 0
∀௣೔ழଶ௡
௣೔ୀଶ
This is because the first term (for ‫݌‬௜ = 2), the sinus will be 0.
We can then also write:
ܲ(2݊ሻ = ෑ sin ൬
ߨ2݊
‫݌‬௜
൰ =
∀௣೔ழଶ௡
௣೔ୀଶ
ෑ ൤sin ൬
ߨ(‫݌‬ + ‫ݍ‬ሻ
‫݌‬௜
൰൨
∀௣೔ழଶ௡
௣೔ୀଶ
= ෑ ൤sin ൬
ߨ‫݌‬
‫݌‬௜
൰ cos ൬
ߨ‫ݍ‬
‫݌‬௜
൰ + sin ൬
ߨ‫ݍ‬
‫݌‬௜
൰ cos ൬
ߨ‫݌‬
‫݌‬௜
൰൨
∀௣೔ழଶ௡
௣೔ୀଶ
= 0
This means that for every 2n>=6, there will be at least one q (≥3 and ≤2n-3) that
will lead to a p equal to 2n-q where the equation between brackets equals to 0 on
an occasion of ‫݌‬௜.
It is this occasion of ‫݌‬௜ that will make the whole product equal to.

5. Author : chrisdecorte@yahoo.com Page 5
To illustrate this with a small example for 2n=20:
The general condition for an equation of type sin ߙ cos ߚ + sin ߚ cos ߙ being equal
to zero is that ߙ + ߚ = ݇ ߨ. In this case, this would mean that p+q should be
divisible by at least one pi where pi takes on all primes from 2 to before 2n.
Already for pi=2, this condition is fulfilled as p+q=2n is an even number.
The above means that we have proven Goldbach’s conjecture.

6. Author : chrisdecorte@yahoo.com Page 6
Step 5: Polignac and general Twin Prime Conjecture
Polignac’s conjecture states: “For any positive even number n, there are infinitely
many prime gaps of size n. In other words: There are infinitely many cases of two
consecutive prime numbers with difference n.”
To highlight that n is even, we will write n as 2n so that 2n=p-q.
Using the previous formula’s, this would mean that we are looking for:
ܲ(2݊ሻ = 0 ; ܲ(‫݌‬ሻ ≠ 0 ; ܲ(‫ݍ‬ሻ ≠ 0
We can then rewrite to: p=2n+q and get:
ܲ(‫݌‬ሻ = ෑ sin ൬
ߨ‫݌‬
‫݌‬௜
൰ =
∀௣೔ழ௣
௣೔ୀଶ
ෑ ൤sin ൬
ߨ(2݊ + ‫ݍ‬ሻ
‫݌‬௜
൰൨
∀௣೔ழ௣
௣೔ୀଶ
= ෑ ൤sin ൬
ߨ2݊
‫݌‬௜
൰ cos ൬
ߨ‫ݍ‬
‫݌‬௜
൰ + sin ൬
ߨ‫ݍ‬
‫݌‬௜
൰ cos ൬
ߨ2݊
‫݌‬௜
൰൨
∀௣೔ழ௣
௣೔ୀଶ
≠ 0
The general condition for an equation of type sin ߙ cos ߚ + sin ߚ cos ߙ being not
equal to zero is that ߙ + ߚ ≠ ݇ ߨ. In this case, this would mean that 2n+q should
not be divisible by not any of the pi where pi takes on all primes from 2 to before
p. This means that there is no prime in between 1 an p or that p itself is a prime..
This means that for every prime q, we can find a corresponding prime p such that
p=q+2n.
Since there are an infinite amount of primes to choose from at the start, it means
that we have proven Polignac’s conjecture.
Remark: nowhere in this prove, there is a hint that n should be less than
70,000,000.

7. Author : chrisdecorte@yahoo.com Page 7
Results
It is clear from the above that our formula for differentiating primes from non
primes is sufficiently strong to prove the existing open conjectures. This is done
using basic trigonometric formula’s and some simple interpretations.
Discussions:
We should try to find the link with Yitang Zhangs work.
Conclusion:
1. Discussing about primes and prime gaps is not so difficult if one uses the
right formula to demonstrate prime.
Acknowledgements
I would like to thank this publisher, his professional staff and his volunteers for all
the effort they take in reading all the papers coming to them and especially I
would like to thank this reader for reading my paper till the end.
I would like to thank my wife for having faith in my work.
References
1. Derivation of a Prime verification formula to prove the related open
problems; Chris De Corte
2. http://en.wikipedia.org/wiki/Polignac's_conjecture