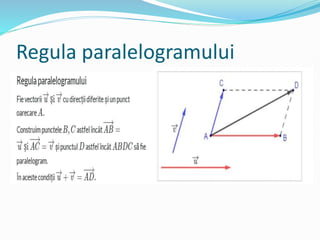
Documentul discută definițiile și operațiile cu vectori, inclusiv segmente orientate și caracteristicile acestora. Se prezintă notarea, lungimea și direcția segmentelor, precum și condițiile de echipolentă pentru segmente. De asemenea, se explică operațiile cu vectori și clasificarea vectorilor în coliniari și necoliniari.

1. Definitia vectorilor
Operatii cu vectori
Vectori coliniari
Calcul vectorial

2. Definiția vectorilor
Segmente orientate
 Un segment [AB] poate fi parcurs în două sensuri,
de la A spre B sau de la B spre A.

3. Definiția 1:
 O pereche ordonată (A,B) de puncte din plan se
numește segment orientat și se notează cu AB.
Punctul A se numește originea,
iar punctul B se numește extremitate, vârful sau
capătul segmentului AB.
Dacă ,A=B, obținem AA care se numește segment
orientat nul.
Observație
Dacă A ≠ B ,atunci [AB]=[BA], dar AB≠BA

4. Definiția 2:
 Lungimea, modulul sau norma unui segment
orientat AB este lungimea segmentului[AB].
Notăm ∣AB∣ sau ∥AB∥.

5. Definiția 3:
 Dreapta suport a segmentului orientat AB este
dreapta .AB.
Direcția unui segment orientat AB este
determinată de dreapta suport, adică de
dreapta .AB.
Spunem că două segmente orientate au aceiași
direcție dacă dreptele lor suport coincid sau sunt
paralele.
Pe fiecare direcție există două sensuri de
parcurs.
Sensul segmentului orientat AB este de
la A spre B, adică de la origine spre extremitate.

6. Definiția 4:
 Două segmente orientate AB și CD se numesc
echipolente dacă au:
- aceiași lungime,
- aceiași direcție,
- același sens.
Notăm AB∼CD.

7. Operații cu vectori
 DEFINITIE
 Fie vectorii u→ și v→ situați în planul P.
Considerăm A un punct oarecare din plan și
punctele B,C astfel încât AB→=u→ și BC→=v→.
Vectorul AC→ se numește suma
vectorilor u→,v→ și se notează u→+v--

8. a) vectori cu direcții diferite (metoda triunghiului)

9. b) vectori cu aceiași direcție și același sens

10. c) vectori cu aceiași direcție, dar cu sensuri opuse

11. Formula lui Chasles
Regula poligonului

12. Regula paralelogramului

13. Vectori coliniari
Definiție:
 Doi vectori care au aceiași direcție se numesc
vectori coliniari.
Doi vectori care au direcții diferite se numesc
vectori necoliniari.

15. Calcul vectorial
Definiție:

17. Teoremă:

18. Profesor coordonator:Farkas Flavius
Elevi: Costea Cosmin Mihai
Fatura Răzvan Pavel
Groza Iacov-Levi
Laurovics Mark-Samuel
Sursa :https://matematicus.net/textbooks/7/chapters/288