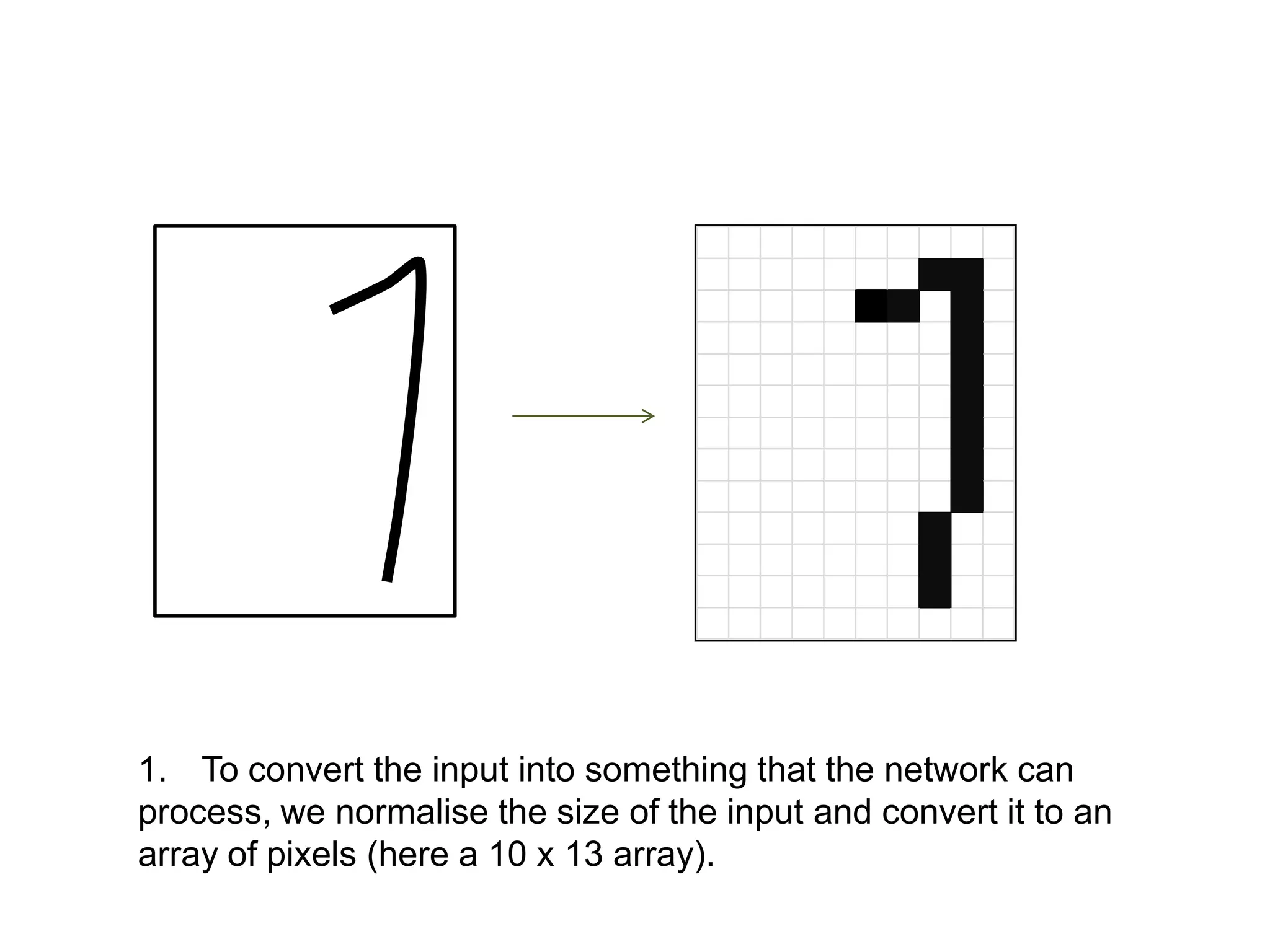
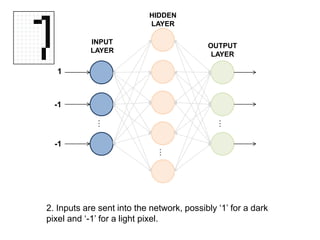
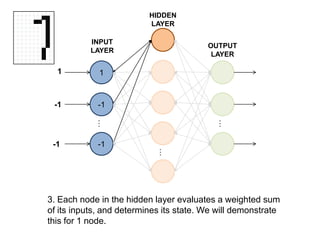
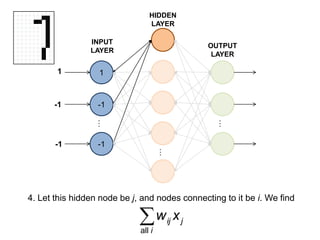
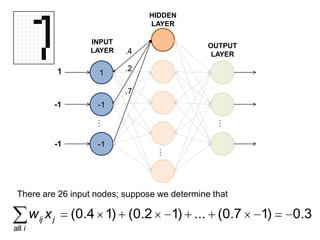
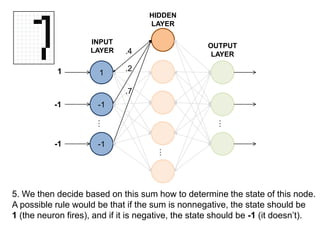
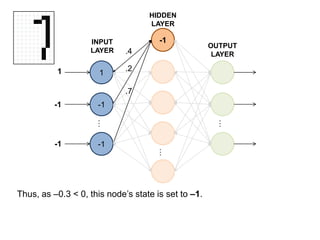
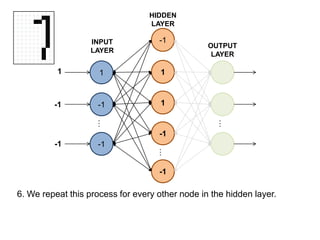
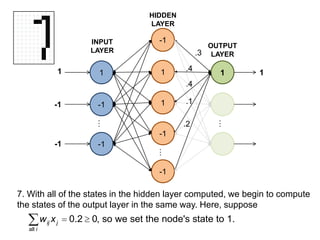
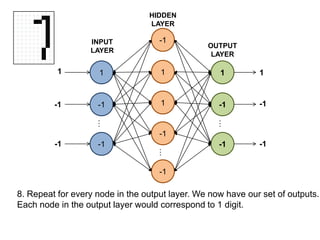
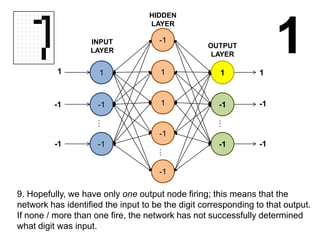
This document summarizes how a basic neural network processes an input image to produce an output classification. It shows how the input is normalized and sent to the hidden layer, where each node calculates a weighted sum of its inputs and determines its activation. The hidden layer outputs are then sent to the output layer, where each node again calculates a weighted sum and activation to determine the final classification. The goal is for only one output node to activate, correctly identifying the input digit.

1. 1. To convert the input into something that the network can
process, we normalise the size of the input and convert it to an
array of pixels (here a 10 x 13 array).

2. HIDDEN
LAYER
INPUT
OUTPUT
LAYER
LAYER
1
-1
…
…
-1
…
2. Inputs are sent into the network, possibly ‘1’ for a dark
pixel and ‘-1’ for a light pixel.

3. HIDDEN
LAYER
INPUT
OUTPUT
LAYER
LAYER
1 1
-1 -1
…
…
-1 -1
…
3. Each node in the hidden layer evaluates a weighted sum
of its inputs, and determines its state. We will demonstrate
this for 1 node.

4. HIDDEN
LAYER
INPUT
OUTPUT
LAYER
LAYER
1 1
-1 -1
…
…
-1 -1
…
4. Let this hidden node be j, and nodes connecting to it be i. We find
w ij x j
all i

5. HIDDEN
LAYER
INPUT
OUTPUT
LAYER .4 LAYER
1 .2
1
.7
-1 -1
…
…
-1 -1
…
There are 26 input nodes; suppose we determine that
w ij x j (0.4 1) (0.2 1) ... (0.7 1) 0.3
all i

6. HIDDEN
LAYER
INPUT
OUTPUT
LAYER .4 LAYER
1 .2
1
.7
-1 -1
…
…
-1 -1
…
5. We then decide based on this sum how to determine the state of this node.
A possible rule would be that if the sum is nonnegative, the state should be
1 (the neuron fires), and if it is negative, the state should be -1 (it doesn’t).

7. HIDDEN
LAYER
INPUT -1
OUTPUT
LAYER .4 LAYER
1 .2
1
.7
-1 -1
…
…
-1 -1
…
Thus, as –0.3 < 0, this node’s state is set to –1.

8. HIDDEN
LAYER
INPUT -1
OUTPUT
LAYER
LAYER
1 1 1
-1 -1 1
…
…
-1
-1 -1
…
-1
6. We repeat this process for every other node in the hidden layer.

9. HIDDEN
LAYER
INPUT -1
OUTPUT
LAYER .3 LAYER
1 1 .4
1 1 1
.4
-1 -1 1 .1
…
…
.2
-1
-1 -1
…
-1
7. With all of the states in the hidden layer computed, we begin to compute
the states of the output layer in the same way. Here, suppose
w ij x j 0.2 0, so we set the node's state to 1.
all i

10. HIDDEN
LAYER
INPUT -1
OUTPUT
LAYER
LAYER
1 1 1 1 1
-1 -1 1 -1 -1
…
…
-1
-1 -1 -1 -1
…
-1
8. Repeat for every node in the output layer. We now have our set of outputs.
Each node in the output layer would correspond to 1 digit.

11. HIDDEN
1
LAYER
INPUT -1
OUTPUT
LAYER
LAYER
1 1 1 1 1
-1 -1 1 -1 -1
…
…
-1
-1 -1 -1 -1
…
-1
9. Hopefully, we have only one output node firing; this means that the
network has identified the input to be the digit corresponding to that output.
If none / more than one fire, the network has not successfully determined
what digit was input.