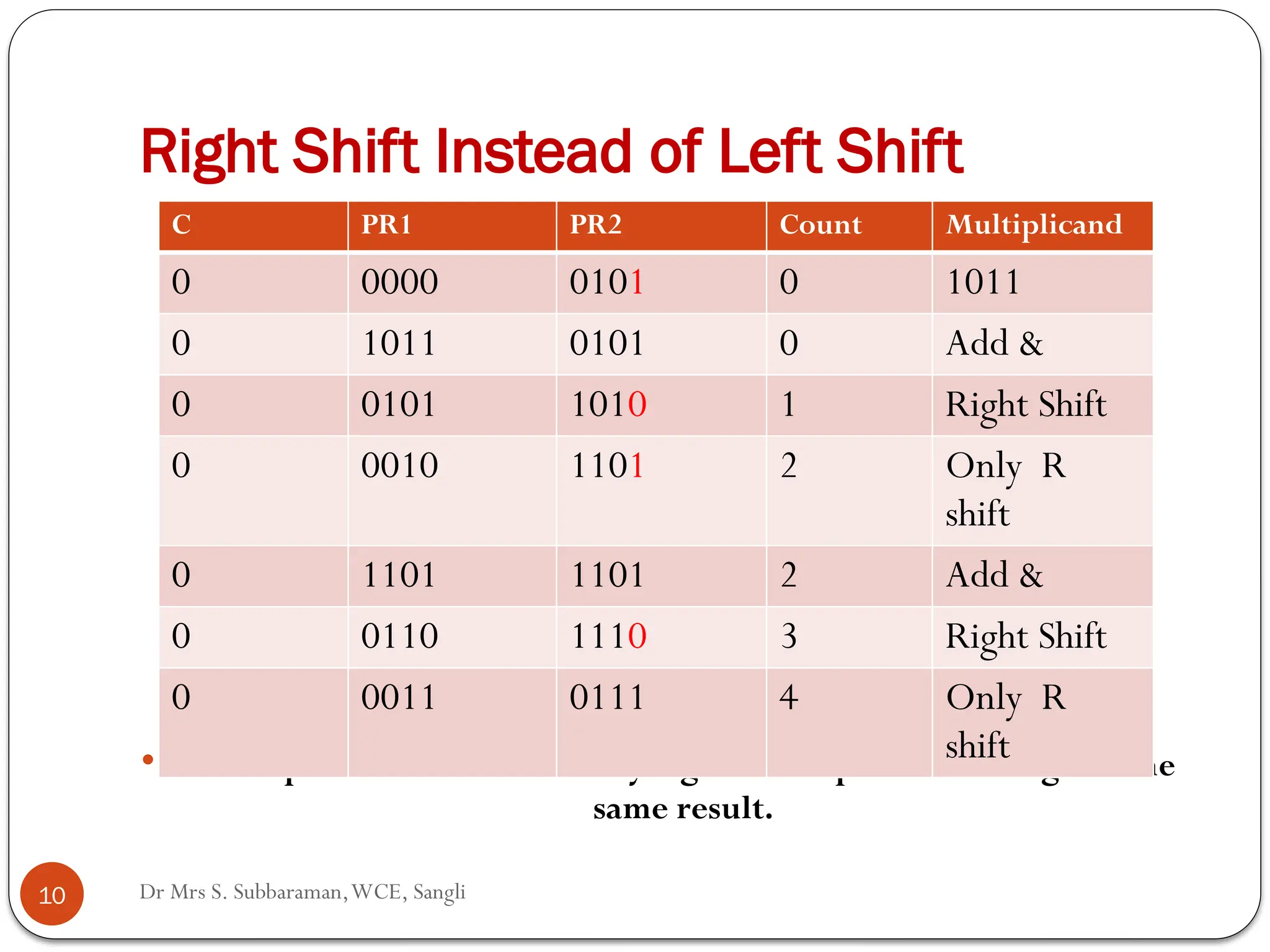
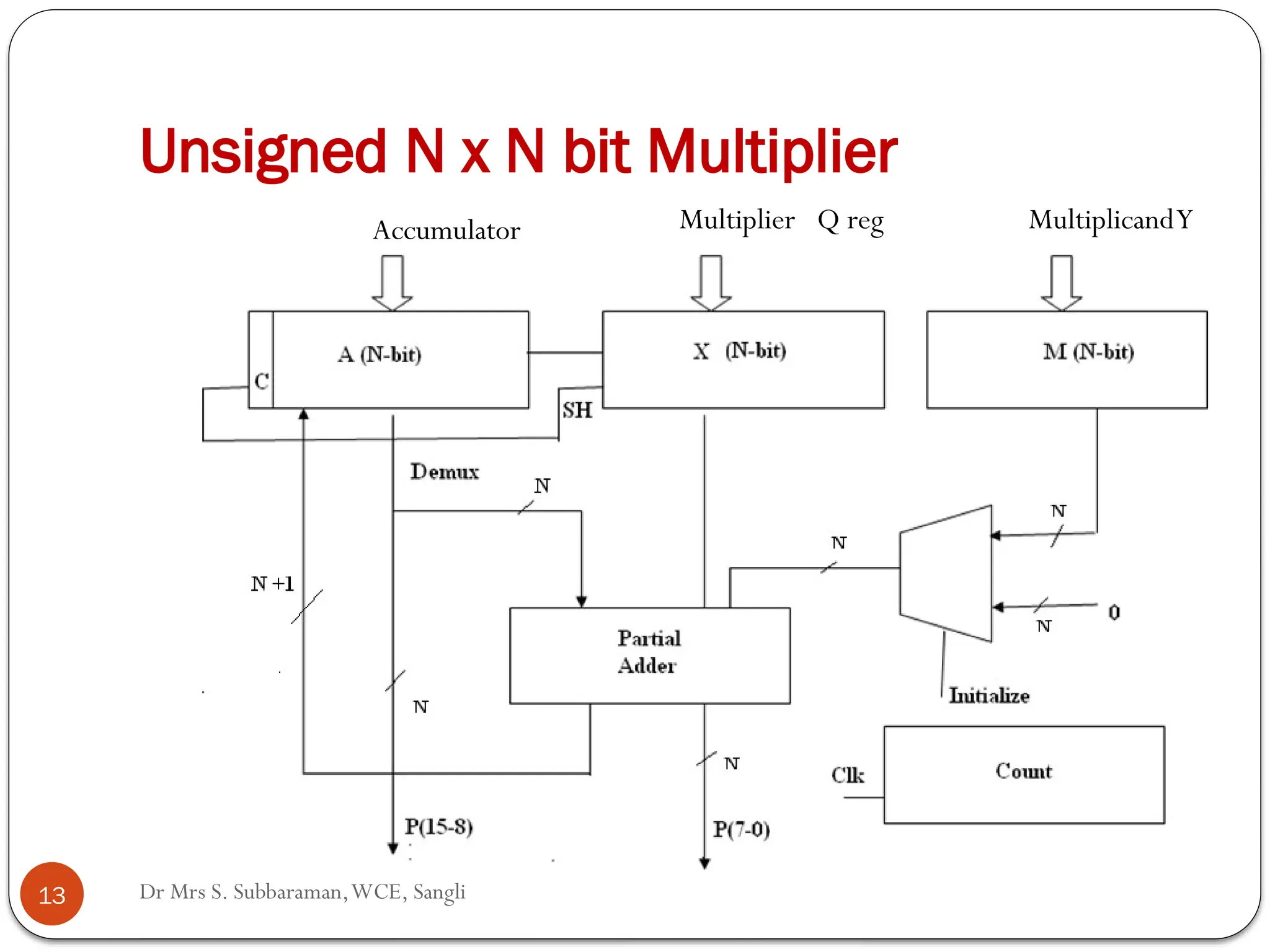
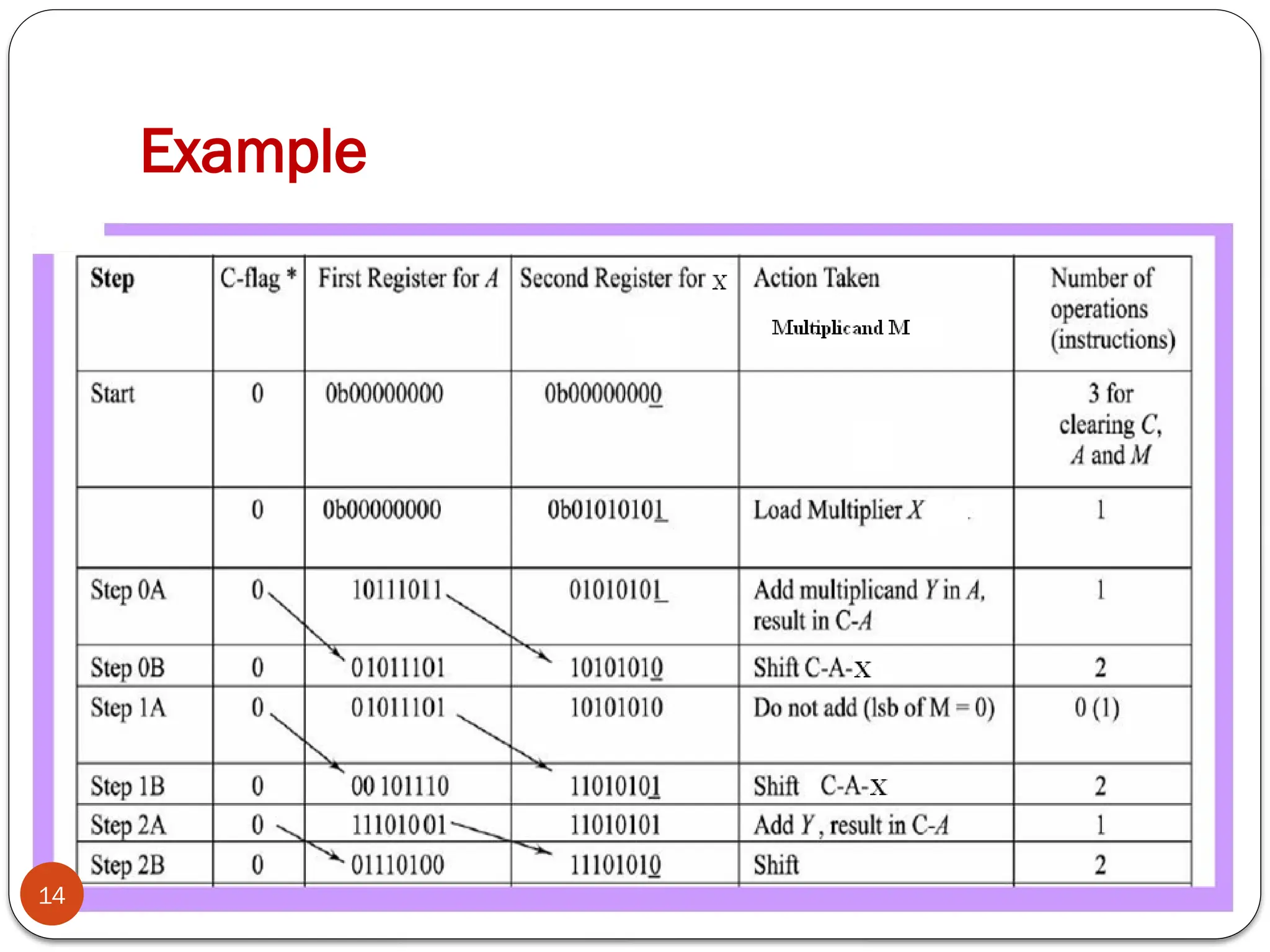
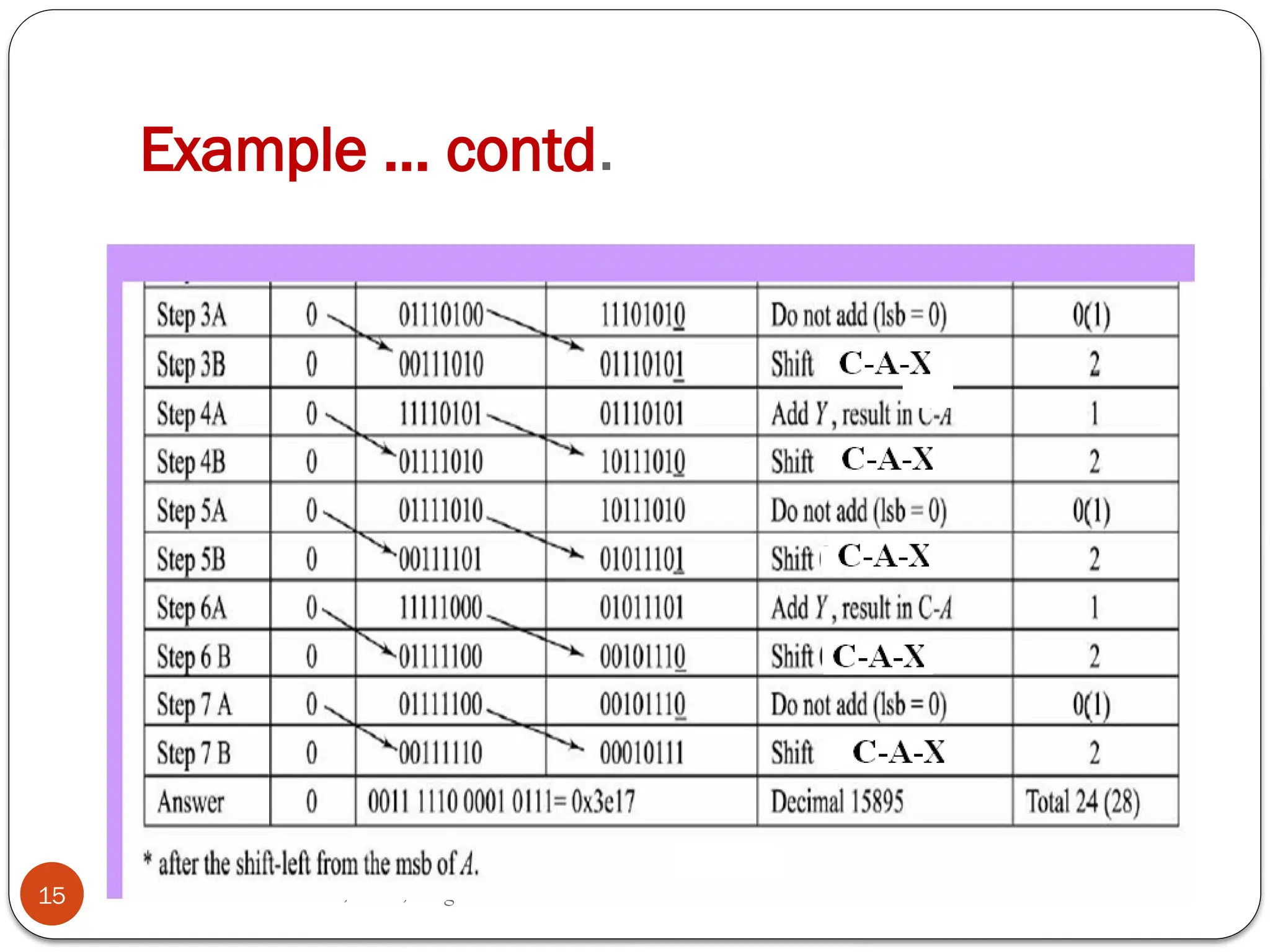
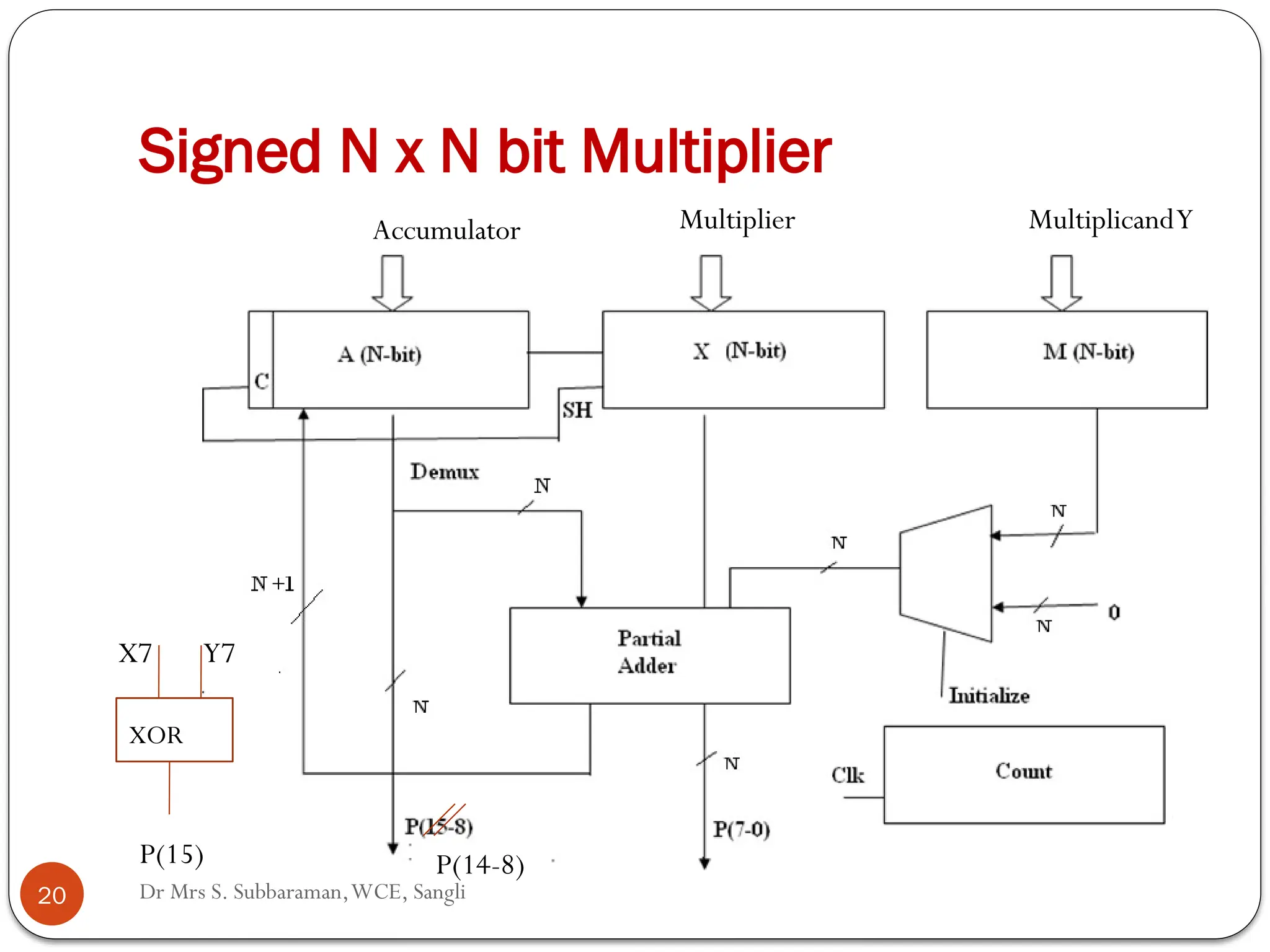
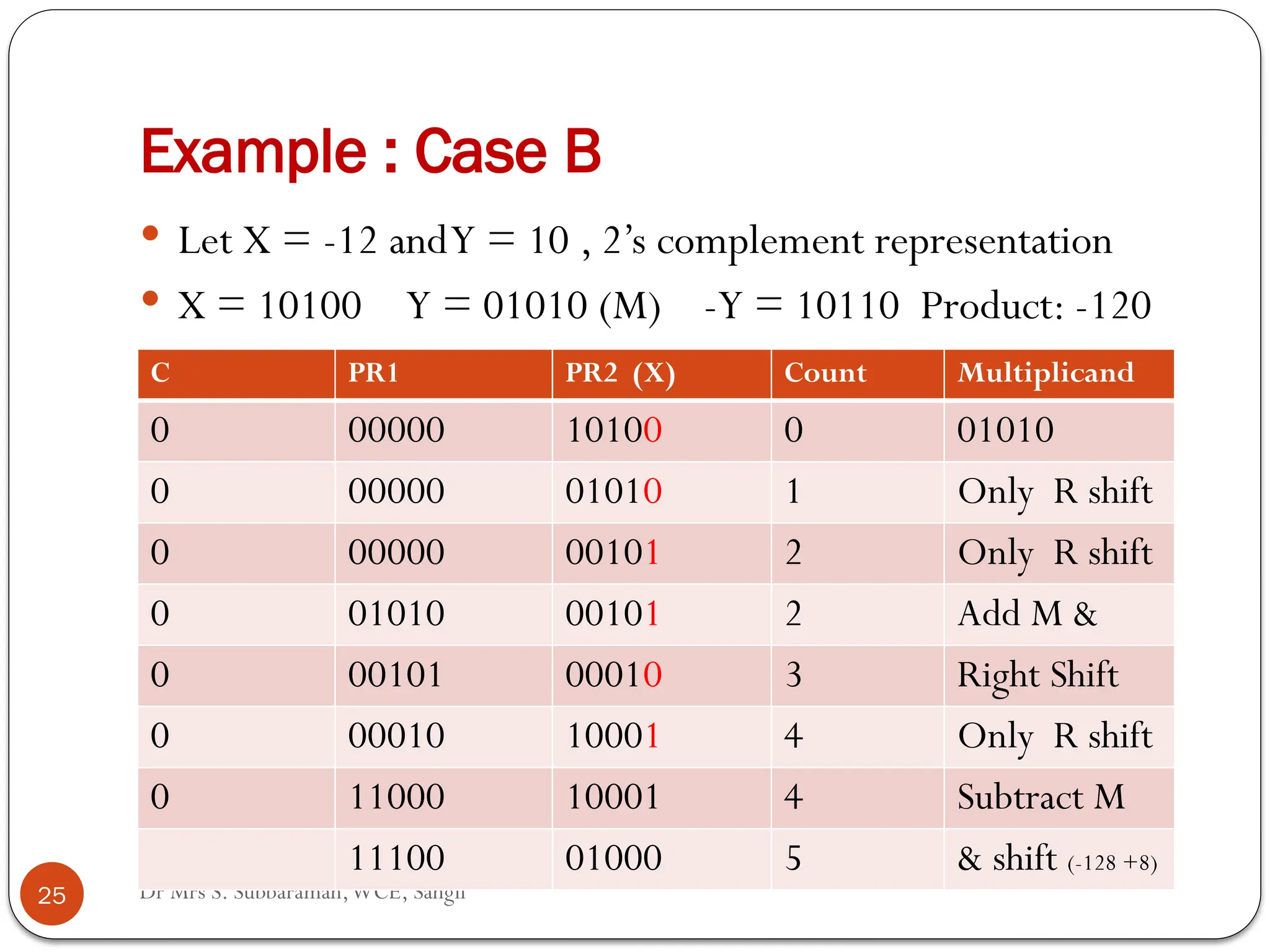
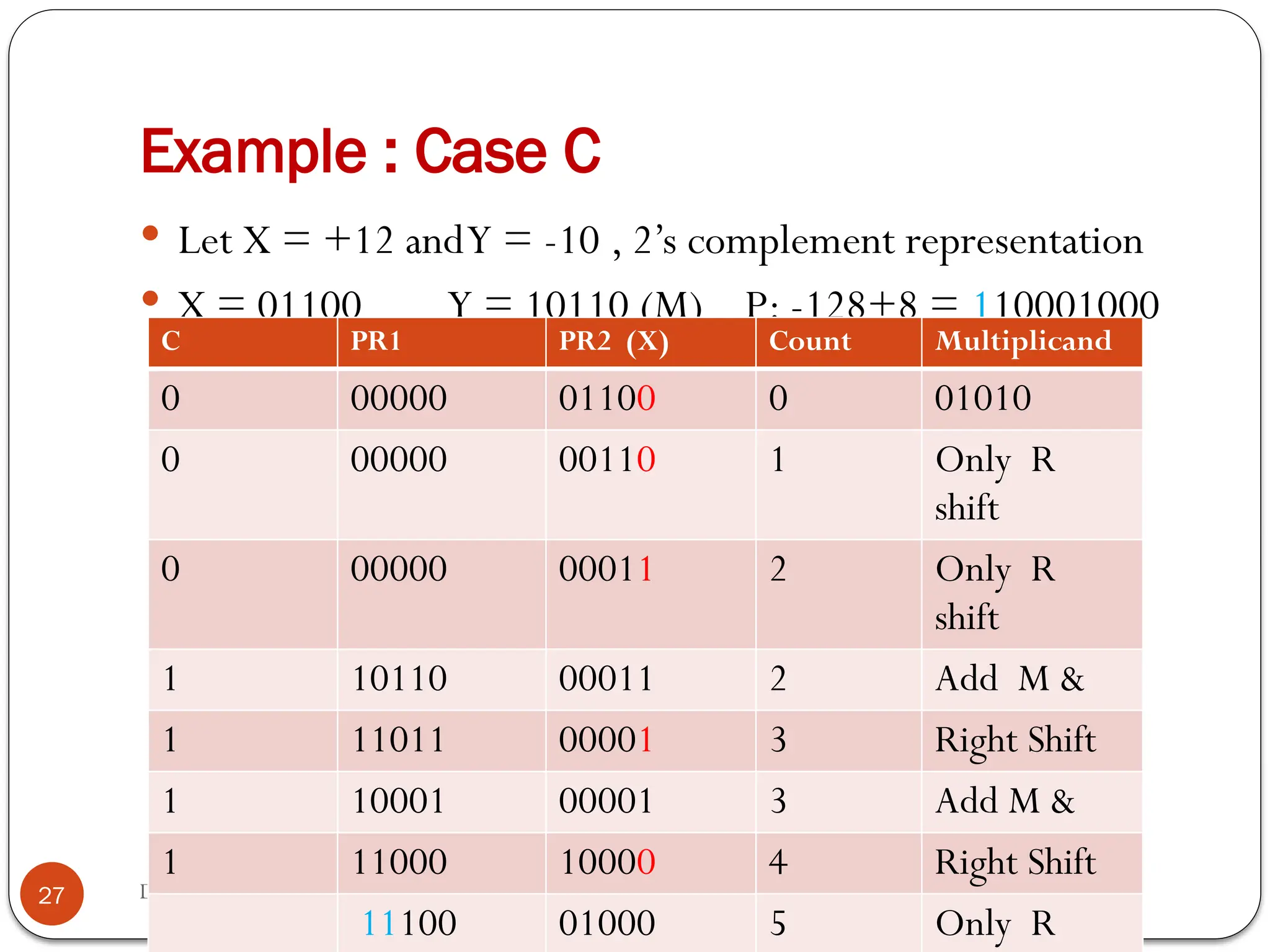
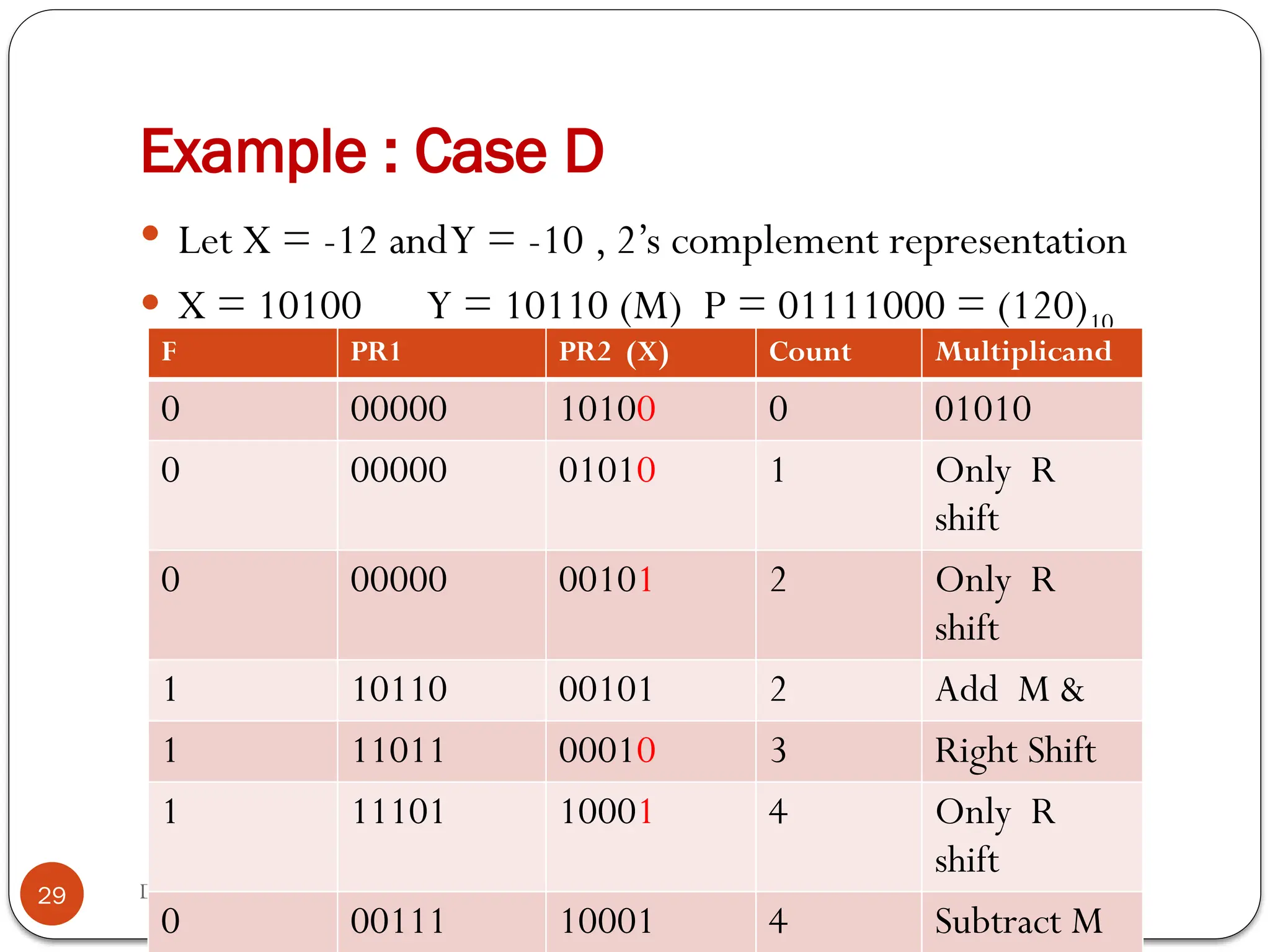
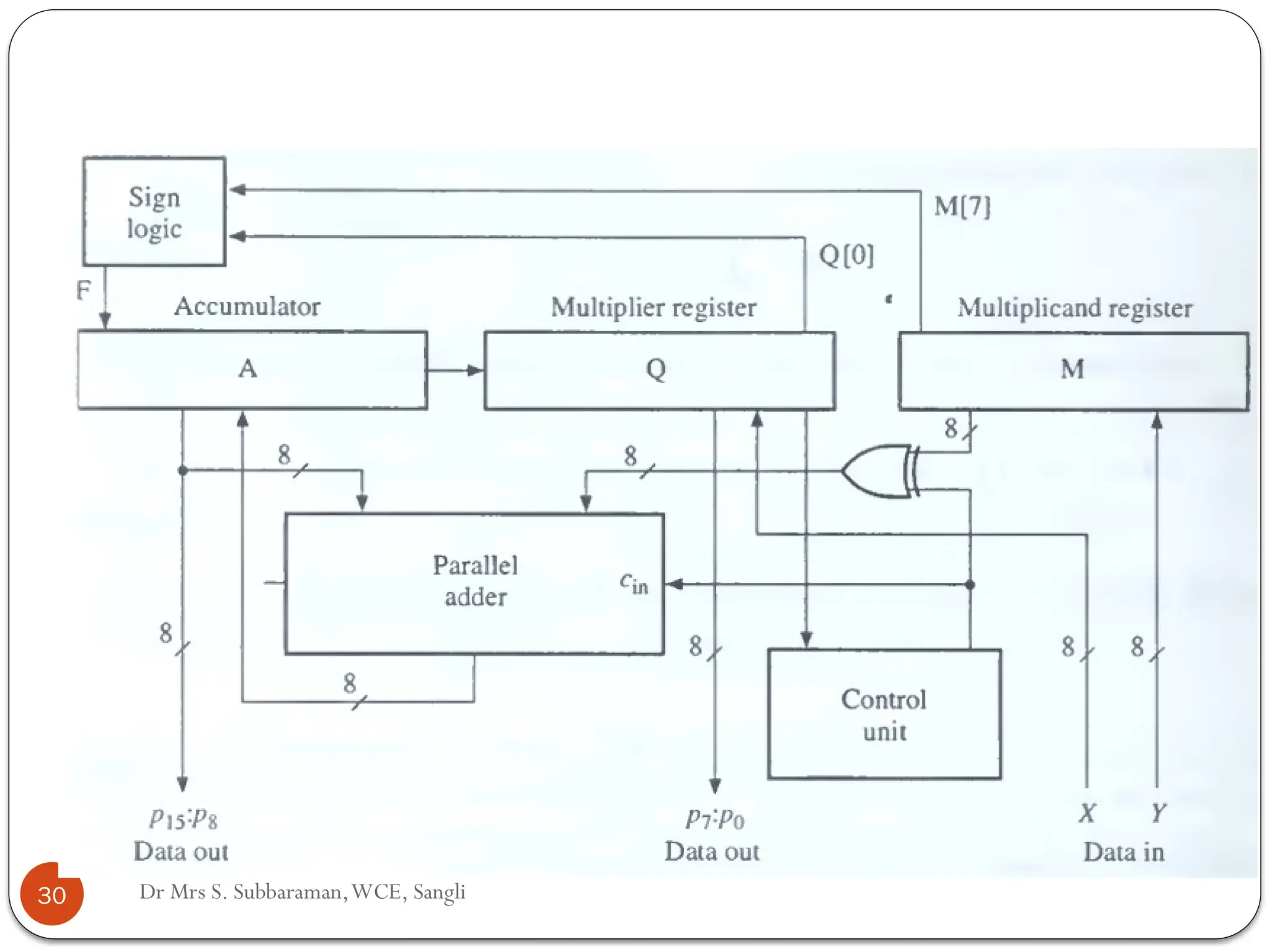
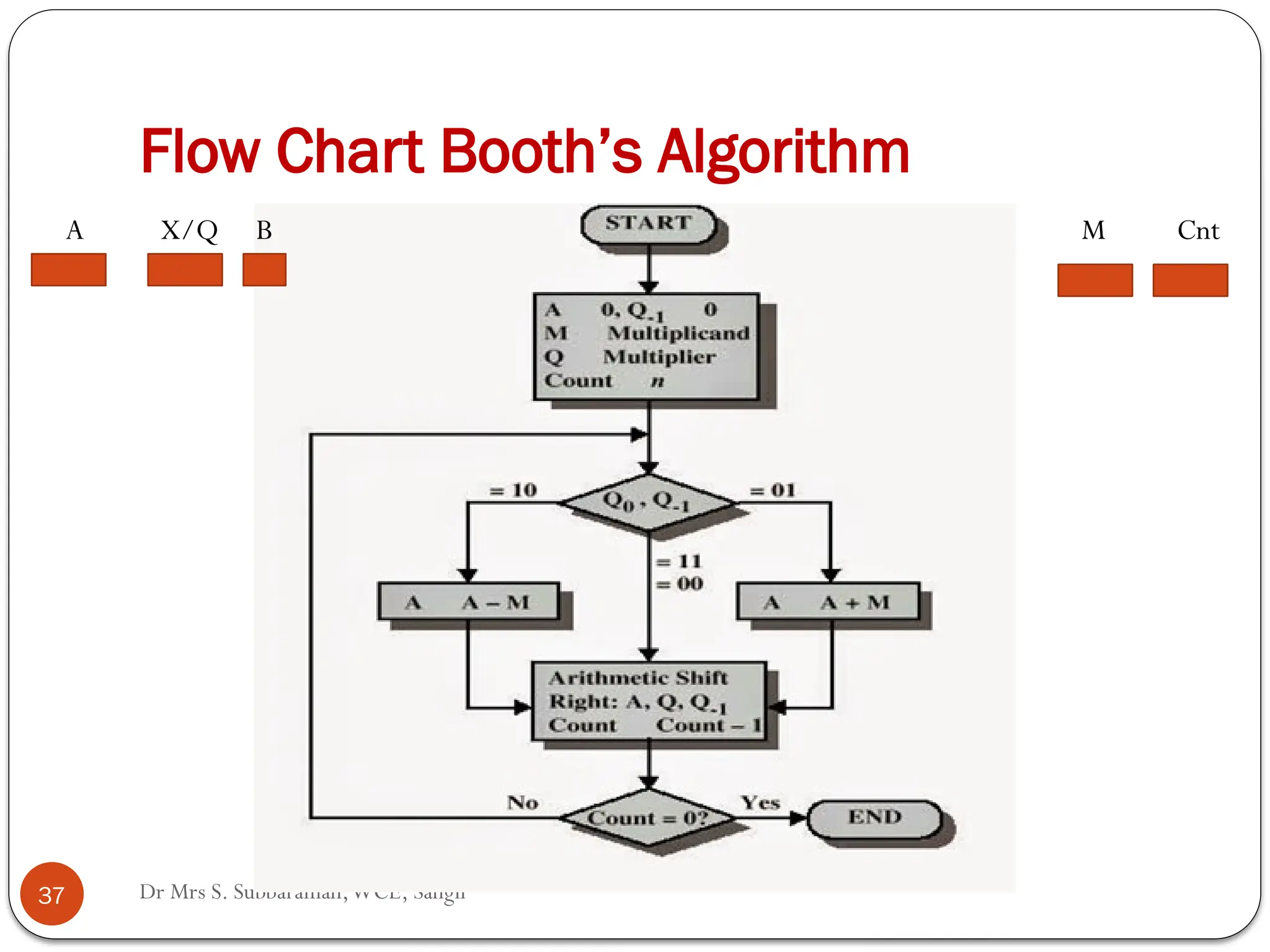
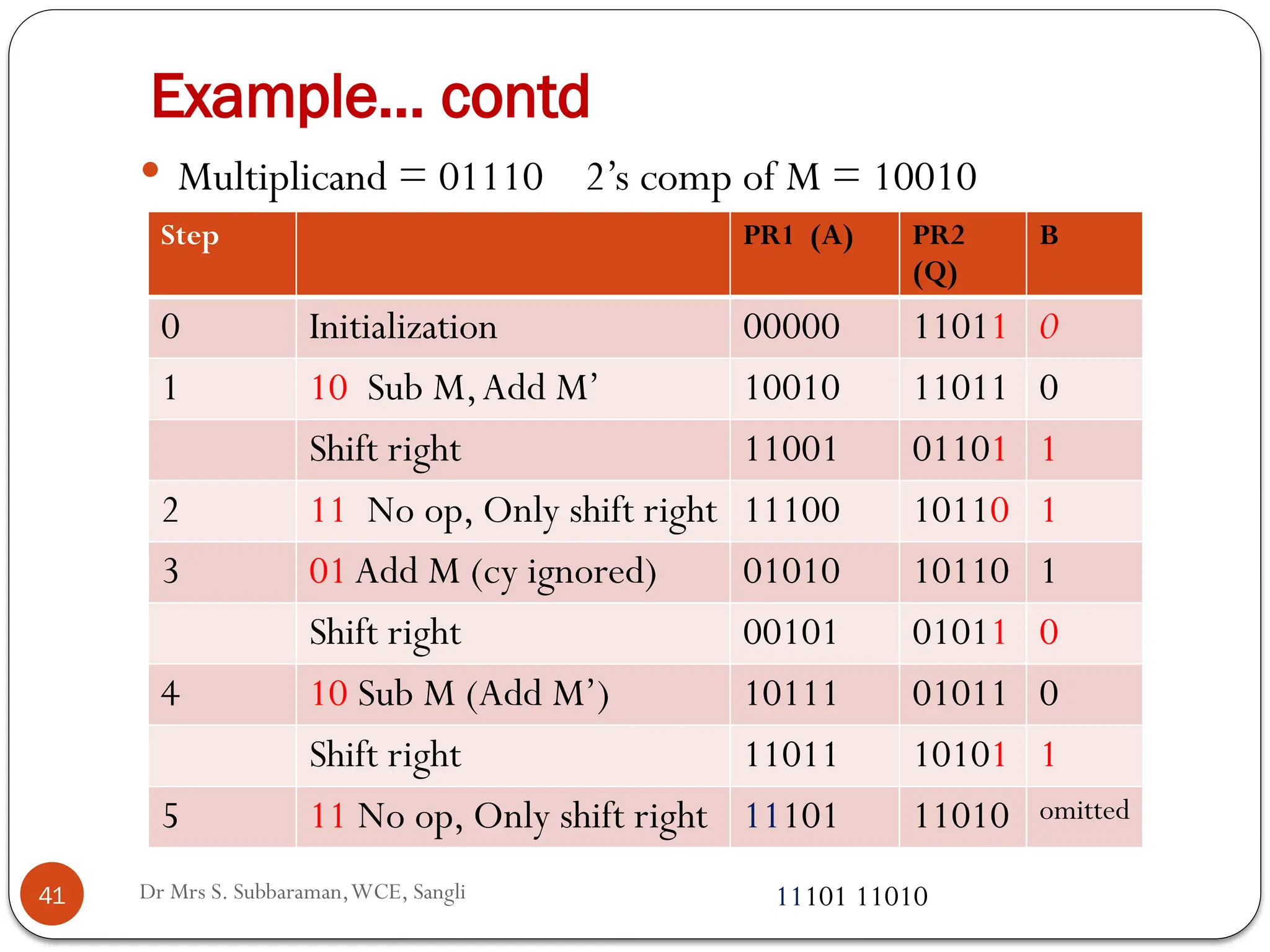
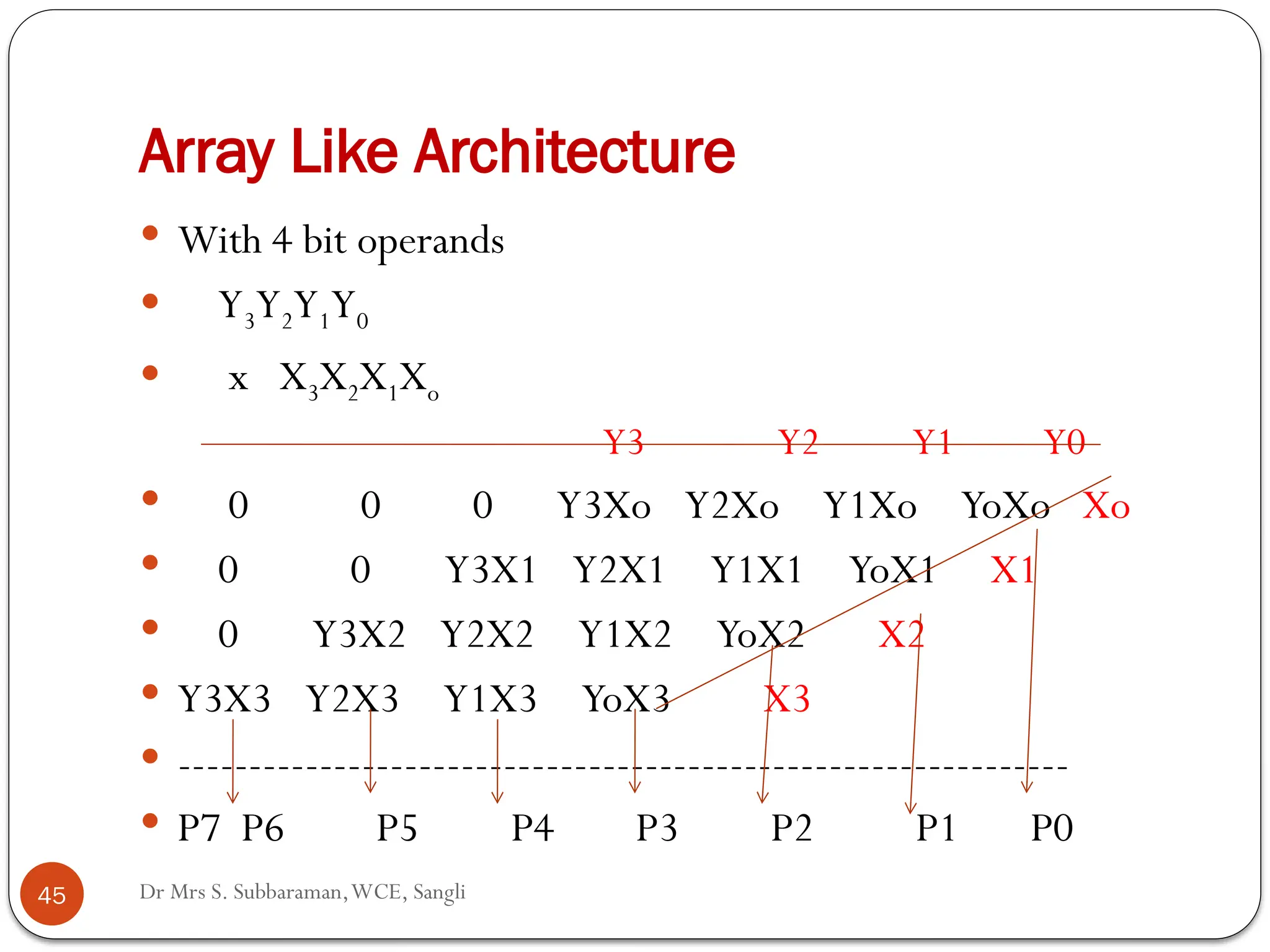
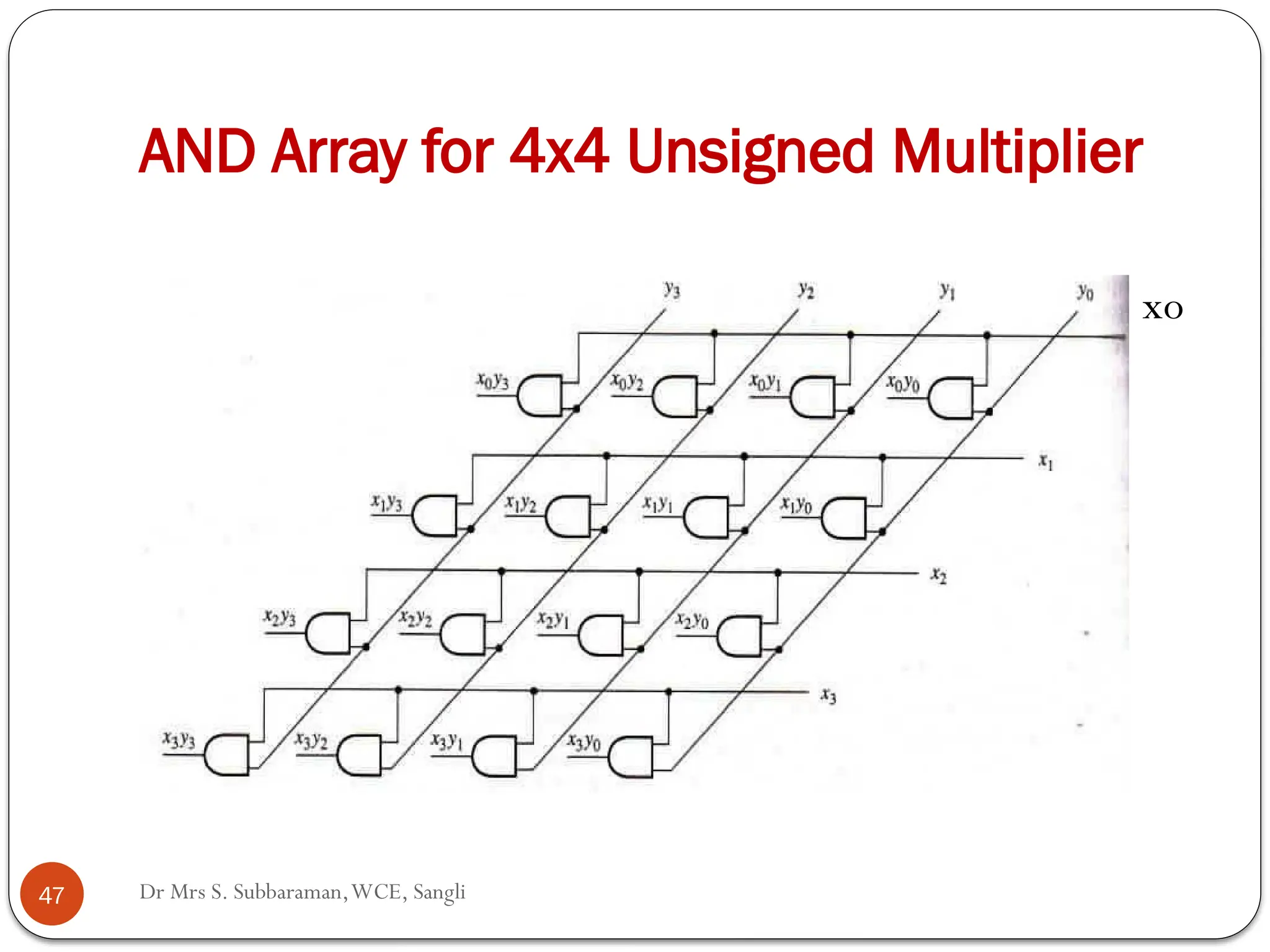
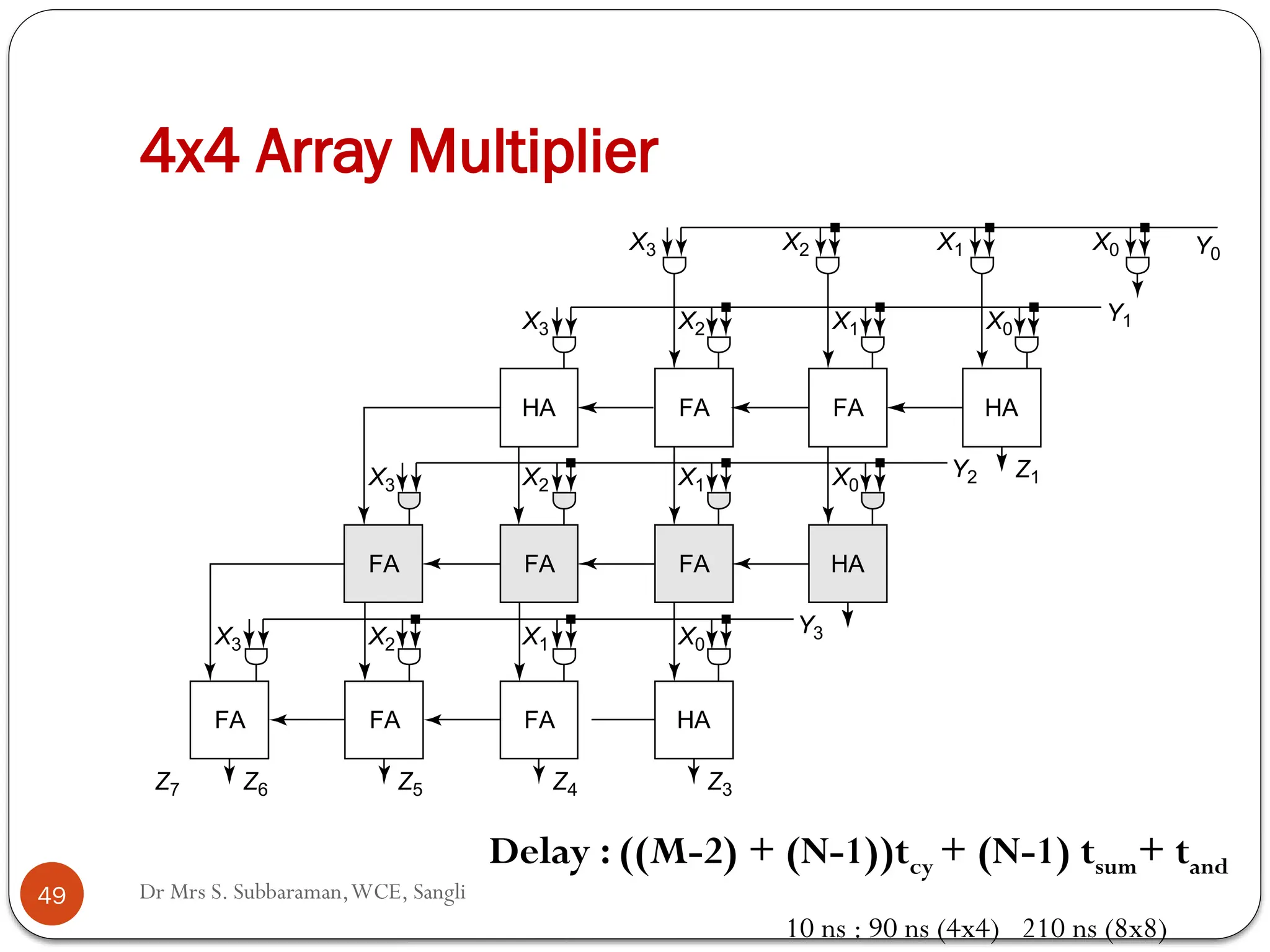
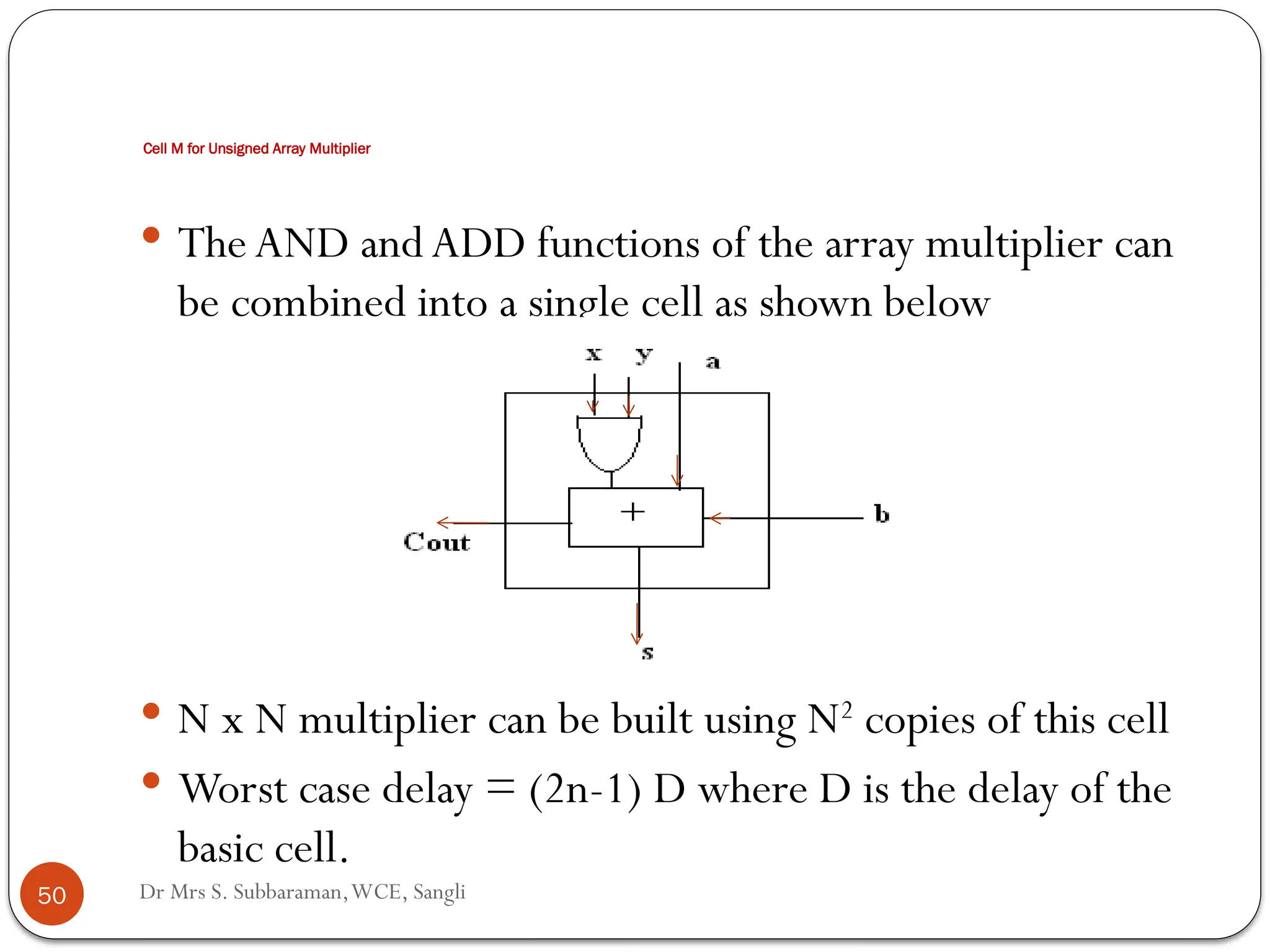
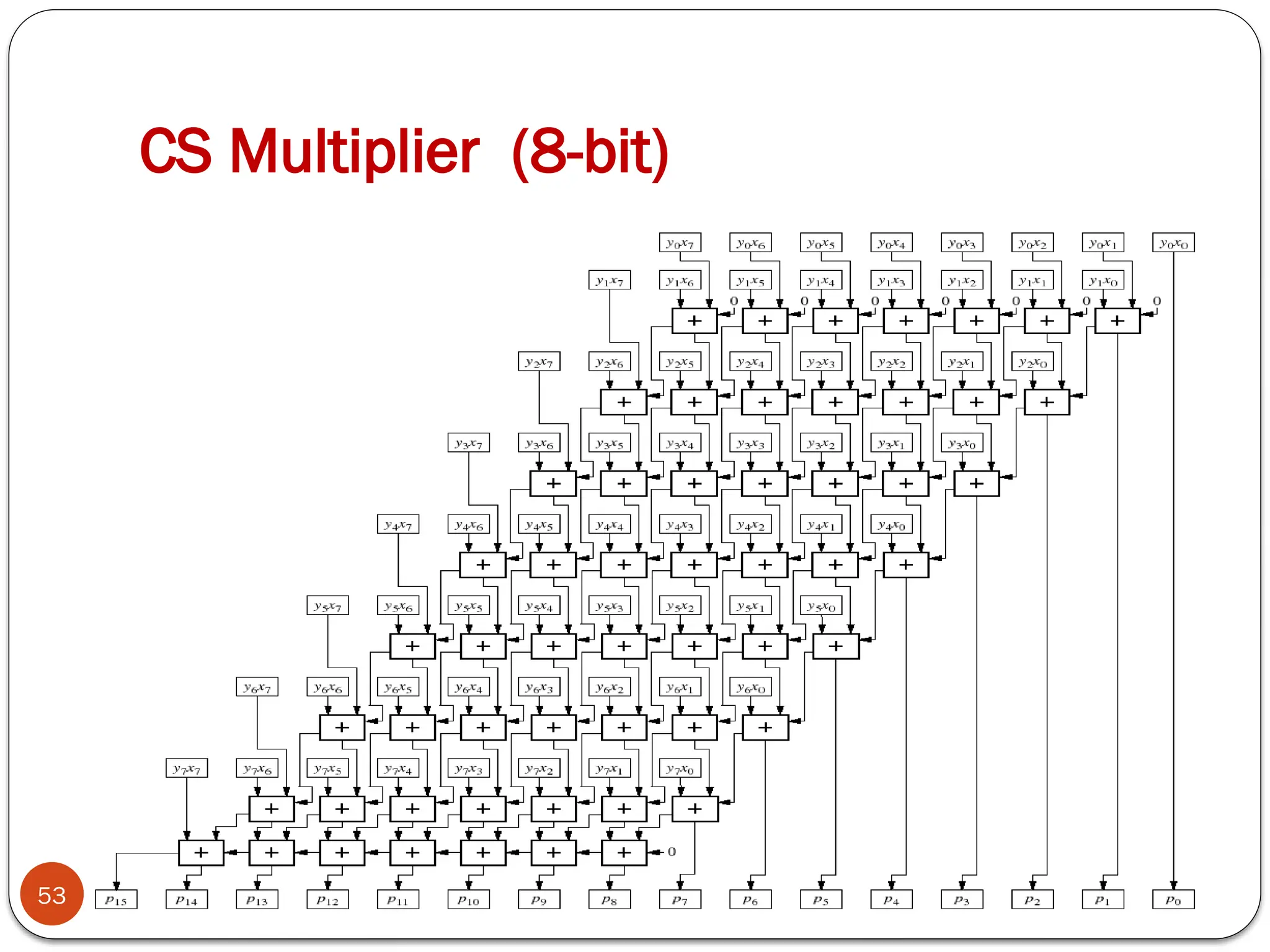
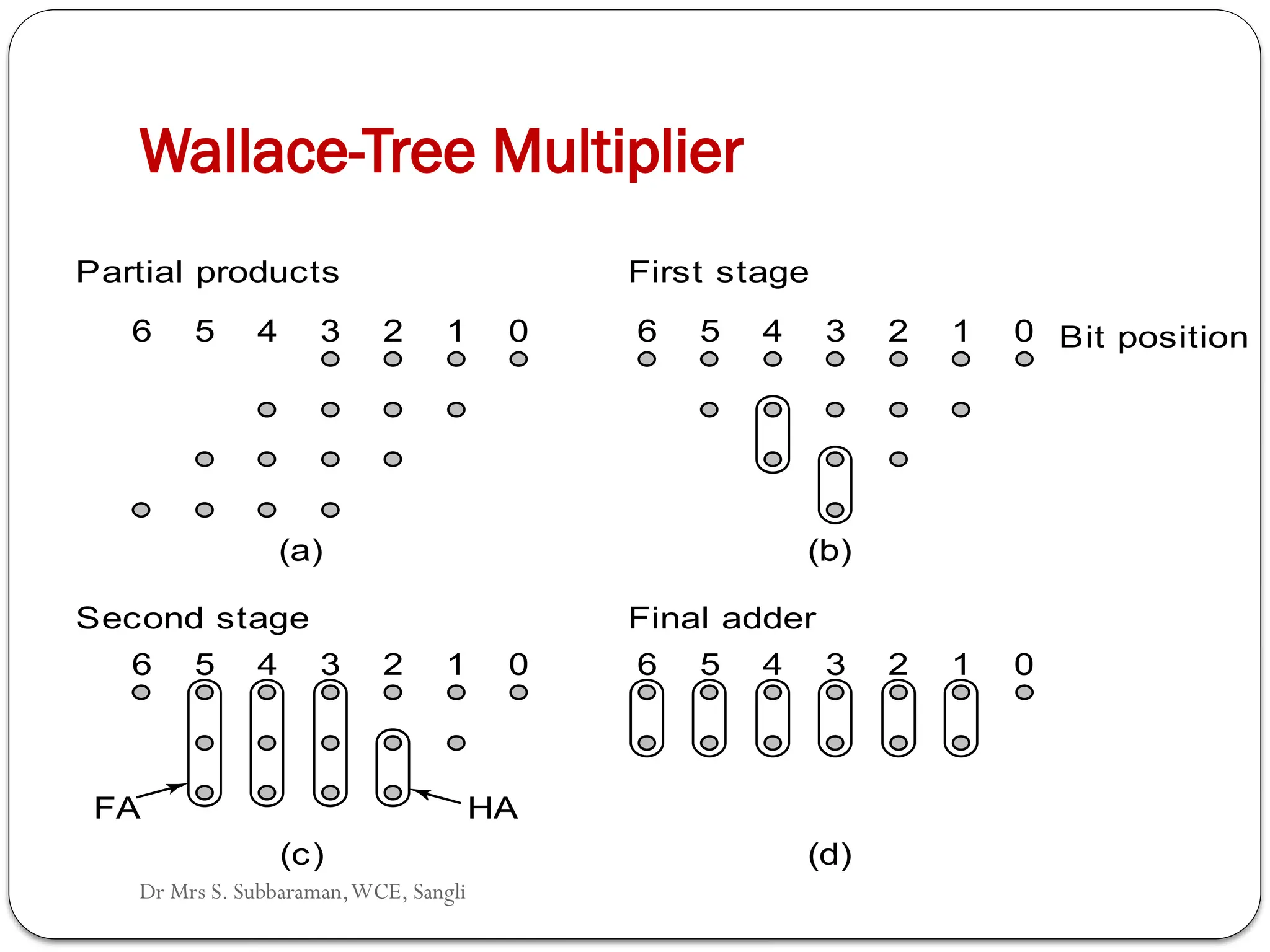
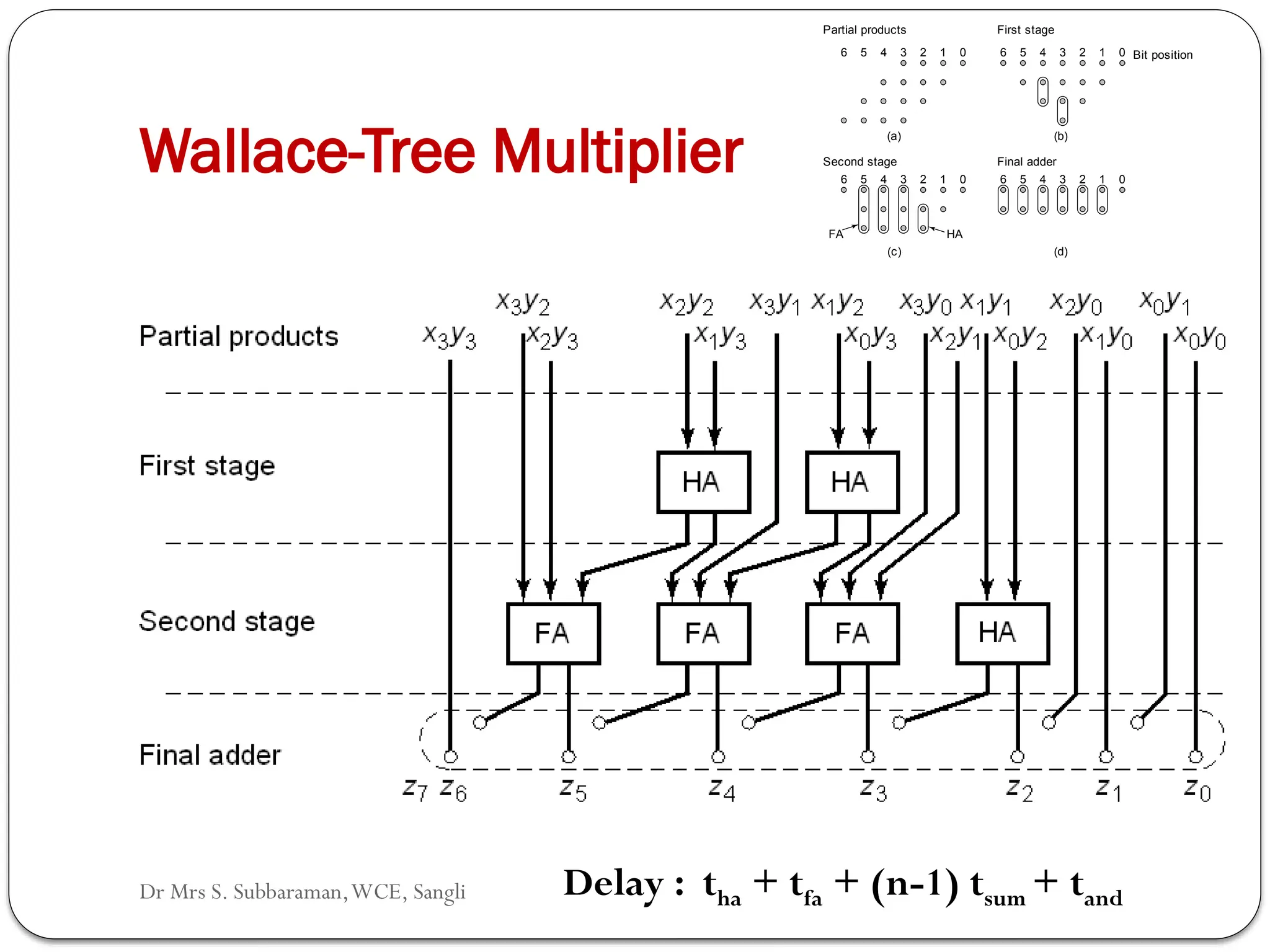
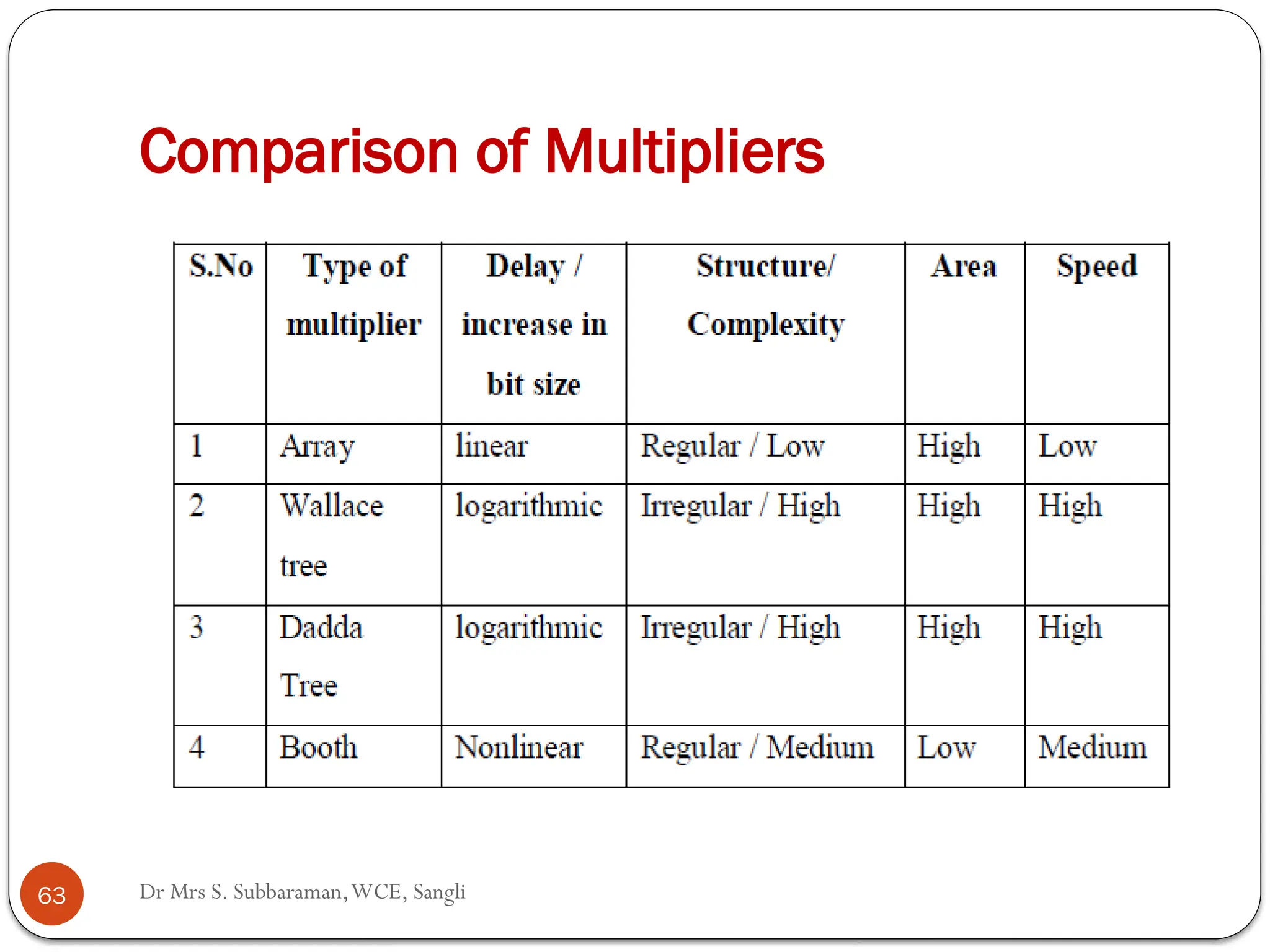
The document discusses various digital multiplier algorithms used in signal processing, covering topics such as unsigned and signed binary multiplication, different multiplier architectures, and algorithms like Booth's and Robertson's. It includes hardware considerations, step-by-step operations for multiplication, and examples of how to handle signed integers using 2’s complement representation. The document provides a comprehensive overview of the principles and applications of digital multipliers in engineering.