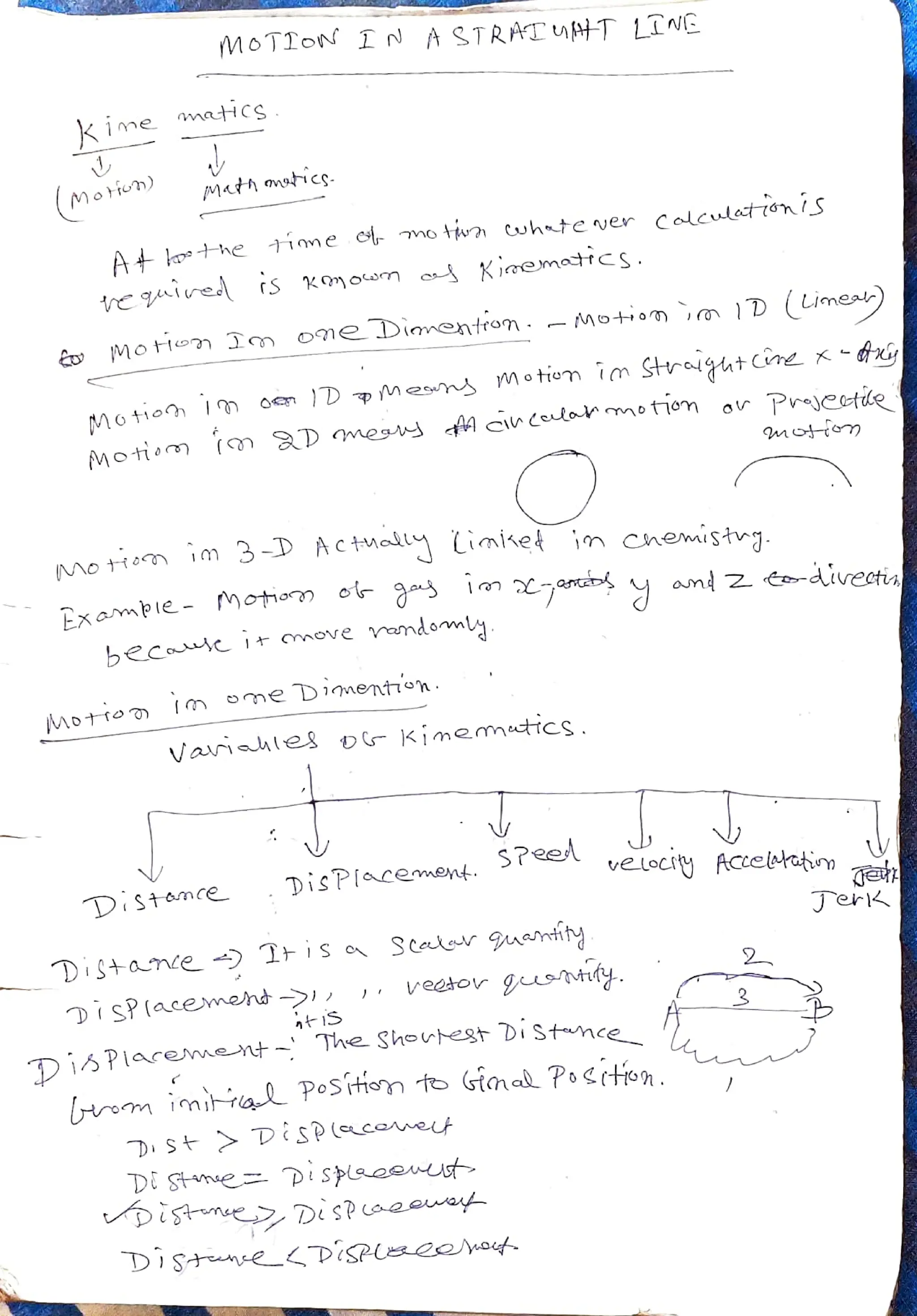
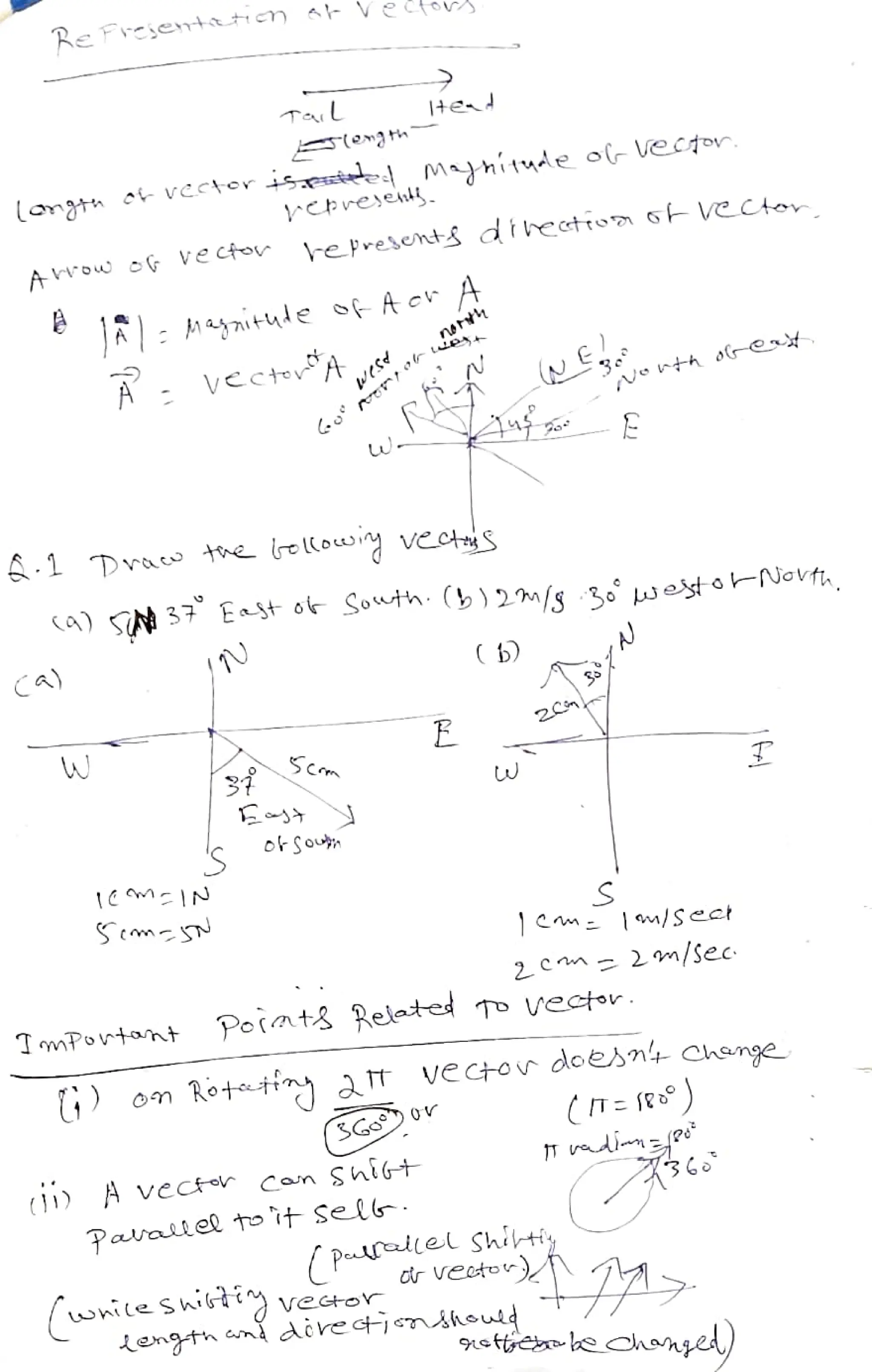
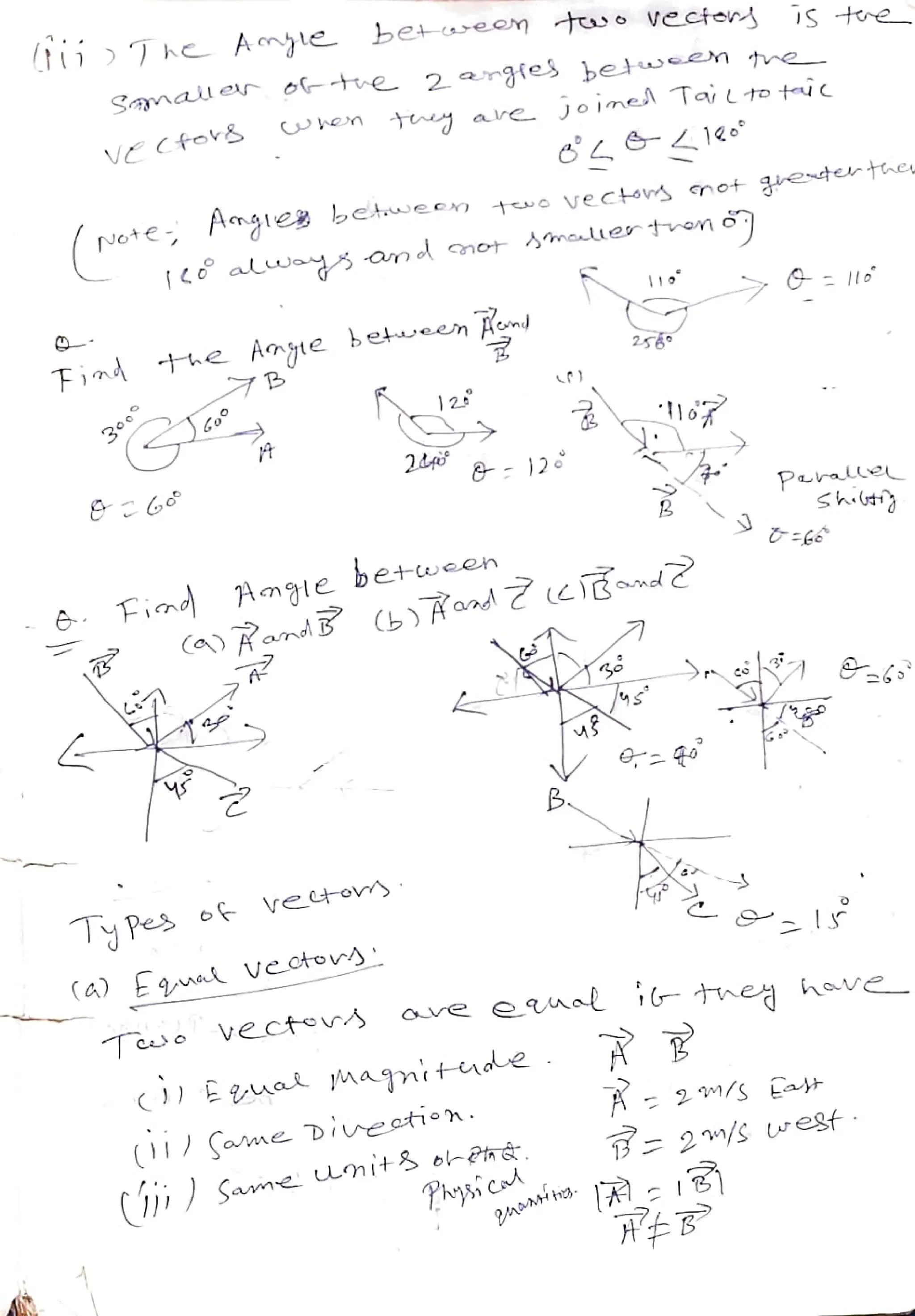
The document discusses the principles of motion, focusing on kinematics, displacement, and vector addition. It covers the concepts of velocity, acceleration, and the methods for vector addition both graphically and analytically. Various mathematical relationships and laws related to vectors are also explored, emphasizing their application in physical contexts.

1. kime
(Motin)
mmatics
Motiom
MoTIoN î N ASTRAT UAT 1TNE
A+ ko the
motro
Math notics
ione
(mD megy A
wcelooton ar
becaeit move vandomy
o mo twa euhteer calculatron S
im 3-D Actmay Cimiet im cnemistg.
Dsteme
( m ome
Dinent.
Vailes
DIS?(acement
DG Kimematics.
DisP[cement.
SPeel
vector gusy.
Pryeetie
DiSParement The Shoutegt Di Stmce
lrminiral PoSthionto sinal Pocton.
D: st> Disp(acevet
DESse Diseent
VDisteDisPaeeat
DiStne<DISPlGNot
velocity Acielratin
and z eodirectia
Jerk

2. (C)
As is Body
diegnul
Pipacemet
wnich
Cammet opPeSte
Covmes
Paticle movey(o
A hoBtwnioh iS th
DiSPiace met opticle.
1mtne
Particle moves
(b) RUS
DSPrcot
(d)2e-1)
A R
(eoacule
AB
A to B
AToB
(rellowiytigve. makes cunaneat cente
a
im any C
ivcie we meve &angle p
S lceef
2R Si m z 2R Sim

3. Gurole ortrcle hasves
betwebN
¡8mce
A and B iS
tnen
TmtneTangie we
tretit R,,R2 ees
Vales my esome but
tivetiunis Ditrevent.
icdívectio iS
divteert Veciris
Dstevent
=2U-cese)
2

4. ,
at
In iericws Chate
() nt.
+o Vecfor
Ailectem
Vectsr 2
thngs (a) unehicul vae
taee wo we Cam
between
iy
mamitde
commbietey we to not nee
Piterenre
and vecter guanty.
Nwmeicl
Valne
(mgmitade)
Pnygica 2uontt. while
Stalarqamiy
need divectsne.
(a)
Nwmerico
vanelMagi
addition.
(b) Diectim.
Vecte Law c
td)tdded
Accovolyto
CKemie DSPlacenn
Can hof lbe
SPeg,
Tembetuie vecto
Law
ot
Adtitn
vefocit, Fovce Acet
vectruanhiy
on.

5. (a)
additin detendS cn
Some +ime
ngles ot 2vectovA
nsi1e
between
two ve cturs arc o b
r e between tuw
Ane
between 2
vectons
ire
cm hen
vetor awe |2:
Note Ac
befeEN tuec2 Vetovs
are
Vector& 1rit attag be vects
guities
aw
tatditfrem ten
jIS
Csalied vector
Vector
dusTlce
magnitde
uentiíag e Diretenjt
Vector
Lawo(-
acdito
AlL
anantei
That
have_
Dineetnare ot
vetov.
ExomPe -
letvic
aurrent
Cuent hy
divectin
betit i
vectov addrt
iavileliegrwmlaw
'of veCtradd
ia
c
vector
gntiy
bemse
Aoest ollow tne Uectur ie.
Srtm.

6. Ca)
retreyent.
A VcctA
A.1 TDra the ollog
Stm
kepresent
dtettua Gh Vecton
Scom
Myitde o ector.
Can snit
TmPontant Po(nt& elated to vectr
() A vectr
Pawalel to it sel.
(6)
Rottin t Ve C+or doen Chenge
(n=se)
2cm m/sec
(wnileswty vector
(
ptrdlelShitiy
cr vector)
Length an dive¢jsnhoud

7. Snaler
VECter&
(Note
ofte 2rg{es between the
Ansle between t o vectos not eterte
Tind the Ange
between
Find Anglebetween
vetos
(a) E ual Ve ctoy
12:
vectos
(07 ame Dieetion.
B
Physicd
256°
Perallel
shiity
eual itney have
B=2/s urest

8. Same Magtude But obpoditeDire tn,
2 m/s East
Parailel am anti- Pohallel vecs.
ISngle
betweem tewota a o
vetor
tien
t t S
Parellel
veltor.
tnecngle
befween tuo taido Ve tsr
lo.
j+is
eallod
nti
Pelellel
veefom.
(o - ine
Vetor
Ve Ctor Lie Sn Seeciome.
alws
KkY tuo
vectrå ie rmte SaePlme.
Tree
tne Some Plae
(e,20)
ormeT be co
[s3,-2

9. (oncuvrent etor
Joso Gr
ore ve 0to
Ve ctors.
A
vector
vecte22roNu vector
dinectinto
j+isavector.
ave
ir A is a nt vetur
|+is
epresnted ay
ACP)
hes rbitvay
imtersectay
Calle Cometrvet
i mte
A
whode nanitdejS
}mity)
Netr.
(A-cat)
sef
Law o r
motia
Tmp)
Whose Magnitude Zere and cwnich
dinectiom It is cd in

10. tjvophical
6 Anaytc metwd.
VeC+r
A4itie Odoitin.
Grathi cel
Cal ethod ot Vector Aldition
Lawo Adårttoy
A
Method ot
Parallal(o9nn
Lawoyaditton
Vechor A
Alitn Deenas
tue Vectv
MeBhoAs ot Veotor Áddifion
Vecer A ditreh
rogo Law
c,fAiditin.
6) Analyticl metted
yect
Vectavtti
(a) erabhical mmethod or veo
tialmethod
twe uile draw vetor shile loiy iesmetiel
meth l.
(Ne wit derive (ormulae whice oy
Amaytical mehed

11. Tvionyle
ve ctr Cah be
then e wiCe et taird Uecto abw
talan
Can nOt bc adde to a vector
( Magnitde
+Dircohion)
Law of Vector Addifron.
(
onetic
Tb
tuo Ve ctur
given bg
veetu.
RadRestont vetov.)
Tttagang e
Lawer
vctsr
AddÍtie
(mgnitude
et ct0 hea
magnitudeo
Diretin)
rebreent
then tre
esltat
is
Srdes o a
tonge im
magnitude amt dirCchie
magitude ond i e ctio teeten io Posite
Lengtn
4ken inSwe rd
mAes'hene tacto head an
tucto head.
he
et thhd Side
adde

12. Exad
A Qirl
120
R 2
Dineihino
nores 3 m tocuar eo
3meast
fen he tkesqo (ettum & novely n
3+
Length
SEae
site
34 2

13. Tuingle Caw Cones
vigutGile
and ?iveel
interseçhonveAtons.
ot teo
ve etos
Manitnde
and dive cttom
4the diagonal
os egom
in
(engt
st
we Shit Evector
B
R
let
tu
are ebvelent
e
and divecin
Cjsine toic
to fic) tuen
given
Qdecent
Sidesota pahaellogain
is
two Vectuv
Delintin
ve ctov& jojmed Tailto t
y
e

14. amd Po(nt a westy whie vector B ha
Fim te magnit ude amd diveotton o
(a) (b)
(oU
. SPecigte Drect
-E.
velat Ve to clue cwet
b.
jonined
RI 2
2o
A+B lou
Soutthok cuest
postiv
Uecto
uovtr wes
-4
+Negatve
Vecto r.

15. AB md A-g hre Some nagitude
Rut distreent bi vetn
Poy°n a wot
vector
Additton
oR
Hendfaic
To add more thontwo Veeterd
the
meto
additrn of Tuainyte
2vete r& a e
hedor c
Tuis b)S
+eo
vectors
weWsed
Parte oayt
Laws e
jnvolued we
Law For
hendo
By
palalelShilty,Briy
Cmorethan
amd Brin) tne teeo r Sec nd vector Kee? t t
hend of lSt
Vector. Bring te

16. DVccter A Aitrm ohey
A
Cammwtatre
Law
(2) v Ctor AdAittn is AMofat R +

17. Pevalleiloguon
ommom
mtersecinPotat
Heve
SiatP
May
divectin
Vectov Additon
4-and NP
) Divecun -
with vel beotto Ve.
B Sine-.
OP
MP
(on)'
R
Nm.
BSin
1f=2
NP2
OPom+mp
+2A BCose
BSin&

18. B Sin
A+BCeJp
f Asin
3+ACoSe
PY Asime
X ACoSO
tan?-IY
A sine
PYLoy
A Sima
(6

19. (oa)o3,
Reswtat
with nhori
(6) jo
G0
Ith
horolznt
(C) o
3o, witn
horoizentl
R:A+B+2AB Cos&
HeleY- |oc)
I two vector
jmcined atGo tnem the
egtttt
)o
|G tneveoe twoeal
Uectov
imclimedata
the reSutnt Bisec tie ng(e Solait Bo, we Can
ProveiF bg
dering
Germla.
AtBCose
loSimGo

20. at 35 rre a vesuetant o 28 N Îh
the anqle ef tueir inclinatoa is Go.Fim
(d) (GN, ao.
28N
2
Here f 3
3x42)2
2g
2 T
2

21. pecial Cases
A
R
A+B+2A B Cose
elne
Vector
Jn Boo
KR A-e
.
Meeimwm alme
ooResatnt
Additren.
we wiL Prure
isovmw
RaThe mani uo
Resultnt wiclbe
1R=A-B R=A~)
|S iwntten
AB2ABcos&
/A+B+2ABx-)
Res<K
1PE ADittere
A-B.ot mor
-t-6)
Rest s als haviny aRnge

22. The Aeinltont ot 3 mits, E-yue.
(a) wnits.
()3hit
tU henever veters
. The
AB+2AB xo'
ane
perendicaulo fo e_l
A4B Cos&
Co)120 vegb
B Sim40 B)
Ato
b.
ten ange betsec,

23. B.
hiCh Poir ot the (ollo borcel
witeerr
Heve
A~R
(a) 2Nand
(6)| Nand t
e The'moycimm
+te
tuso ven
Vetent or
17wnit&-,an 7 mit2, vePeti
at riqratieTD
Ueetove are
tne
hagnitude
oGtueir
vejultant -
(019
I994-2s
magnitude s
Vectovk e
Rin
tiey
AB -TAB

24. Yuo boves aCng at
andte menieo teir heluttat
(C)13,v
te
Magnitnde ob bohes2
Let s
Wethod-)
2A+B+2ABcoSe
4tundc Bsina
AtBCoso
Undene!
a Doint IS IR
asme HIS malloer
Divisin
gnitude,
B-t
Re l2
AZB
CA-B)(A+B)2XAxB
t+B=)My
2A-A)
Bcoset

25. .(a)&36
(omo
B
Ve ctoro
B Find
o t t
u
e nyte
iSeacel
it hall te Maghitude
Vector
A and It3 e
or two vetovd
A and BS
lt
La
A
et Very micely
B
íne
B
result
nt
)<x (Bf)
B-A)
6+A)(B-A)
The
when
(22/
Metod-2