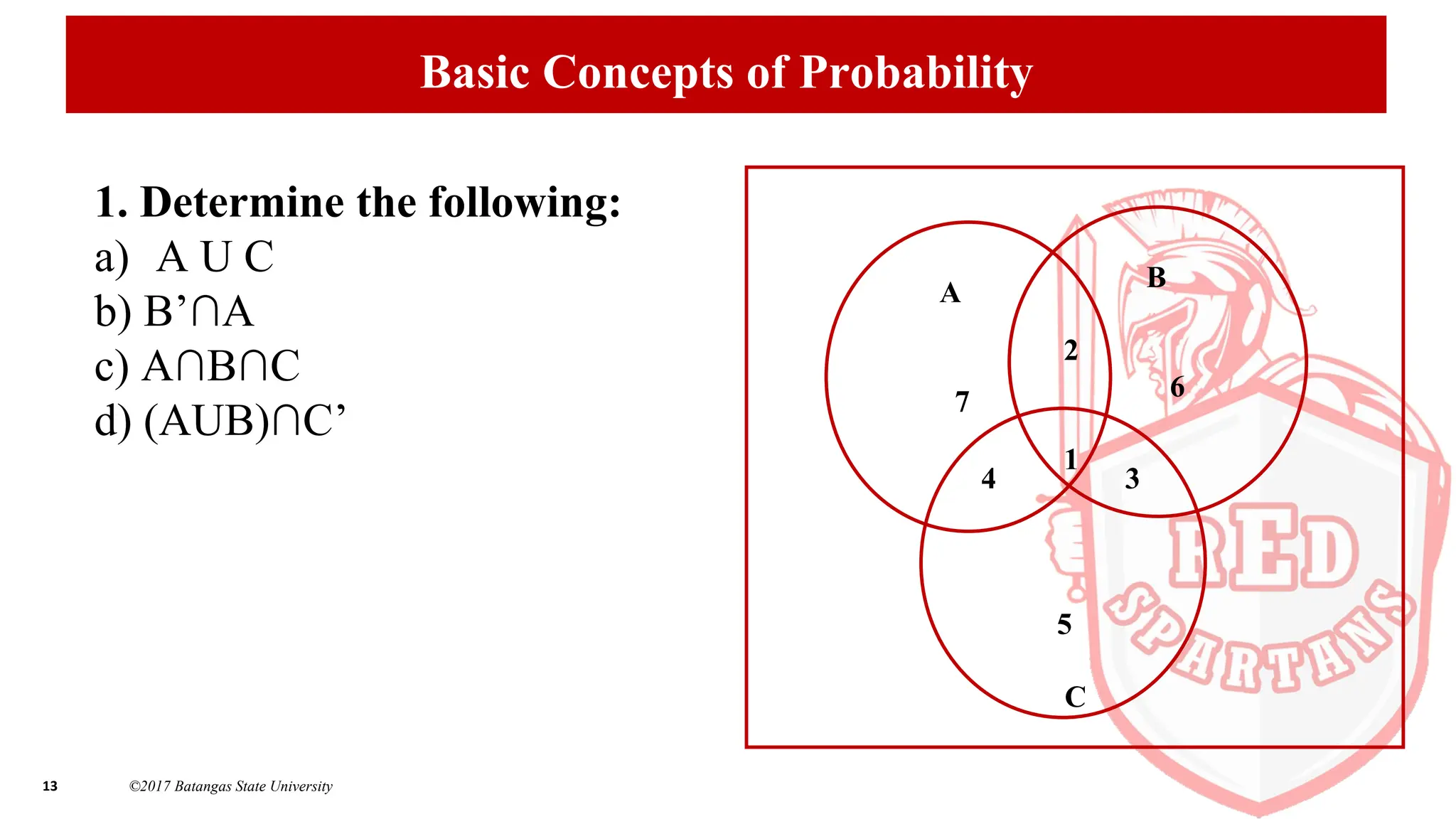
This document provides an overview of basic statistical concepts and probability principles. It defines key terms like sample space, event, intersection of events, union of events, and complement of an event. Examples are given to illustrate these concepts. The document also discusses counting sample points using theorems and formulas for permutations and combinations. Finally, it covers the probability of an event occurring and provides examples to calculate probabilities.