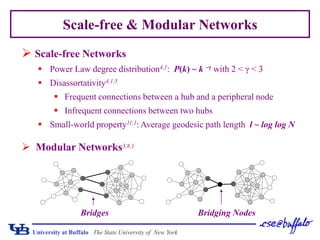
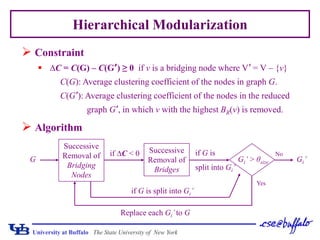
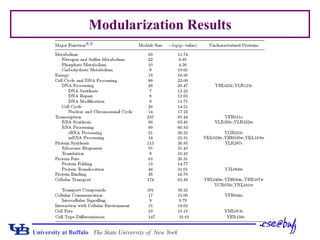
This document presents a method for assessing hierarchical modularity in protein interaction networks. The method involves successively removing bridging nodes and bridges from the network to split it into hierarchical modular subgraphs. Applying the method to a protein interaction network of Saccharomyces cerevisiae revealed four zones of node removal corresponding to bridging, interconnecting, core, and peripheral nodes. Analysis found that bridging and interconnecting nodes were less lethal but more important than peripheral nodes, while core nodes were the most lethal. The modularization results divided the network into hierarchical communities.

1. University at Buffalo The State University of New York
Young-Rae Cho, Woochang Hwang, Murali Ramanathan
and Aidong Zhang
State University of New York at Buffalo
Assessing Hierarchical Modularity
in Protein Interaction Networks

2. University at Buffalo The State University of New York
Scale-free & Modular Networks
 Scale-free Networks
 Power Law degree distribution4,1: P(k) ~ k –γ with 2 < γ < 3
 Disassortativity4,1,5
 Frequent connections between a hub and a peripheral node
 Infrequent connections between two hubs
 Small-world property11,1: Average geodesic path length l ~ log log N
 Modular Networks3,8,1
Bridges Bridging Nodes

3. University at Buffalo The State University of New York
Bridge Measurement
 Global Measurement
 Betweenness Centrality7:
 Local Measurement
 Clustering Coefficient11:
 Neighbor Significance: ,
 Similarity of Nodes:
 Combined Bridge Measurement
 Bridging Nodes:
 Bridges:

4. University at Buffalo The State University of New York
Hierarchical Modularization
 Constraint
 ∆C = C(G) – C(G’) ≥ 0 if v is a bridging node where V’ = V – {v}
C(G): Average clustering coefficient of the nodes in graph G.
C(G’): Average clustering coefficient of the nodes in the reduced
graph G’, in which v with the highest BR(v) is removed.
 Algorithm
Successive
Removal of
Bridging
Nodes
Successive
Removal of
Bridges
if ∆C < 0 if G is
split into Gi’
G Gi’ > θsize Gi’
No
if G is split into Gi’
Yes
Replace each Gi’to G

5. University at Buffalo The State University of New York
Topological Analysis
 Data: Core protein interaction data of Saccharomyces cerevisiae from DIP10,2
 Method: Remove v with the highest BR(v) and compute C(G), iteratively.
 Results:
 I & II (~ 30%): Bridging and interconnecting node removal zone.
 III (~ 30%): Core node removal zone.
 IV (~ 40%): Peripheral node removal zone.

6. University at Buffalo The State University of New York
Biological Analysis
 Data: Core protein interaction data of Saccharomyces cerevisiae from DIP10,2
 Method: Remove a set S of nodes v with the highest BR(v) and
compute the proportion of lethal proteins in S, iteratively.
 Results:
 Bridging and interconnecting nodes are less lethal than core nodes.
 Bridging and interconnecting nodes are more lethal than peripheral nodes.

7. University at Buffalo The State University of New York
Modularization Results
6,9

8. University at Buffalo The State University of New York
References
1. Barabasi, A.-L. and Oltvai, Z. N., Nature Reviews: Genetics (2004)
2. Dean, C. M., Salwinski, L., Xenarios, I. and Eisenberg, D., Molecular and Cellular
Proteomics (2002)
3. Hartwell, L. H., Hopfield, J. J., Leibler, S. and Murray, A. W., Nature (1999)
4. Jeong, H., Mason, S. P., Barabasi, A.-L. and Oltvai, Z. N., Nature (2001)
5. Maslov, S. and Sneppen, K., Science (2002)
6. Mewes, H. W., at al., Nucleic Acid Research (2006)
7. Newman, M. E. J., Physical Review E (2001)
8. Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z. N. and Barabasi, A.-L., Science
(2002)
9. Ruepp, A., at al., Nucleic Acid Research (2004)
10. Salwinski, L., at al., Nucleic Acid Research (2004)
11. Watts, D. J. and Strogatz, S. H., Nature (1998)