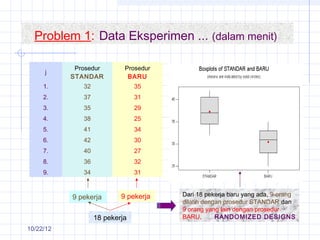
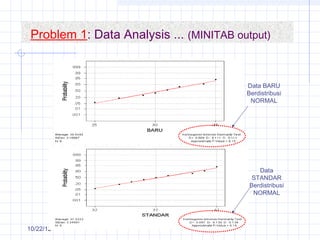
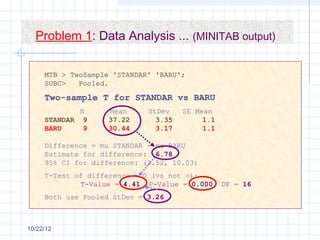
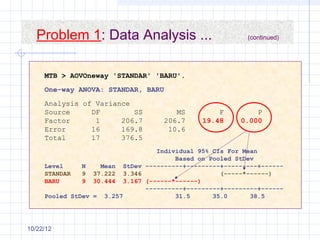
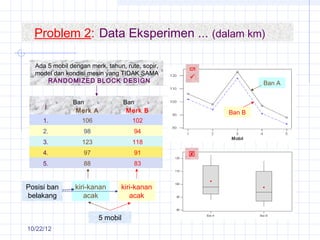
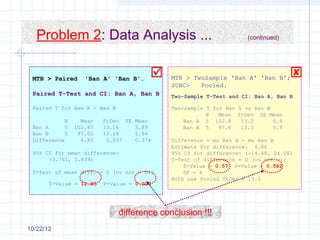
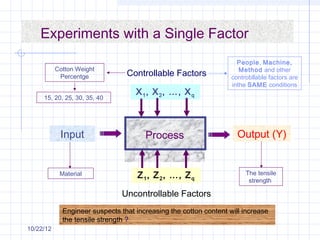
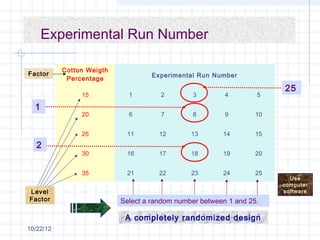
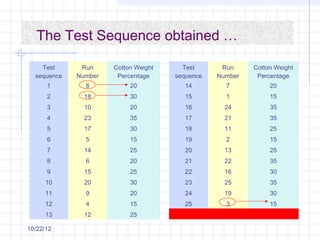
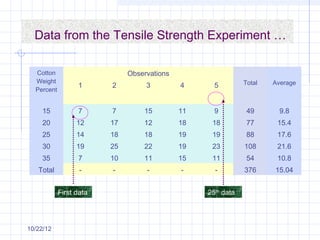
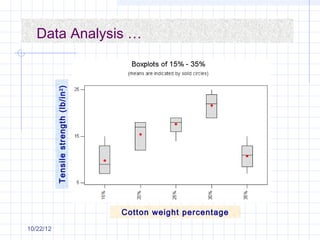
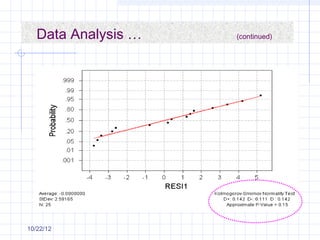
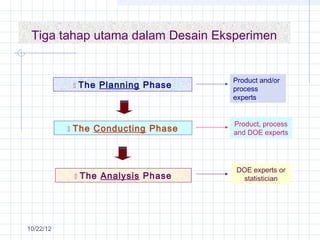
The document discusses different types of experimental designs, including simple comparative experiments, experiments with a single factor, randomized complete block design, Latin square design, and factorial designs. It provides examples of problems involving comparative experiments between two production procedures and between two tire brands. It demonstrates the process of collecting data, performing statistical analyses like t-tests, ANOVA, and Tukey's test to analyze the results and determine if there are significant differences between groups. The key steps in experimental design are planning, conducting, and analysis phases.

1. Materi : DOE Minggu II
1. Introduction
2. Simple Comparative Experiments 
3. Experiments with a Single Factor
4. The Randomized Complete Block Design
5. The Latin Square Design
6. Factorial Design
7. The 2 k Factorial Design
8. Two-Level Fractional Factorial Design
9. Nested or Hierarchial Design
10. Response Surface Methods
10/22/12

2. Reference :
. Montgomery, D.C. (2003)
Design and Analysis of
Experiments
Fifth Edition, John Wiley & Sons.
 Chapter 2. Simple Comparative Experiments
 Inferences About the Defferences in Means :
 Randomized Designs
 Paired Comparison Designs
 Inferences About the Variances of Normal Distributions
 Chapter 3. Experiments with a Single Factor: The Analysis
of Variance
 Completely Randomized Designs
10/22/12

3. Problem 1: Simple Comparative Experiments
Manusia, Mesin dan
Metode perakitan faktor lain yang dapat
produk Controllable Factors dikontrol dalam kondisi
SAMA
X 1 , X 2 , …, X q
Prosedur Prosedur
STANDA BARU
R
Input Process Output (Y)
Bahan baku Z 1 , Z 2 , …, Z q Waktu perakitan
produk produk
Uncontrollable Factors
Apakah ada perbedaan rata-rata waktu perakitan produk antara
prosedur STANDAR dan BARU ?
10/22/12

4. Problem 1: Data Eksperimen ... (dalam menit)
Prosedur Prosedur
j
STANDAR BARU
1. 32 35
2. 37 31
3. 35 29
4. 38 25
5. 41 34
6. 42 30
7. 40 27
8. 36 32
9. 34 31
9 pekerja 9 pekerja Dari 18 pekerja baru yang ada, 9 orang
dilatih dengan prosedur STANDAR dan
9 orang yang lain dengan prosedur
18 pekerja BARU. RANDOMIZED DESIGNS
10/22/12

5. Problem 1: Data Analysis ... (MINITAB output)
Data BARU
Berdistribusi
NORMAL
Data
STANDAR
Berdistribusi
NORMAL
10/22/12

6. Problem 1: Data Analysis ... (MINITAB output)
MTB > TwoSample 'STANDAR' 'BARU';
SUBC> Pooled.
Two-sample T for STANDAR vs BARU
N Mean StDev SE Mean
STANDAR 9 37.22 3.35 1.1
BARU 9 30.44 3.17 1.1
Difference = mu STANDAR - mu BARU
Estimate for difference: 6.78
95% CI for difference: (3.52, 10.03)
T-Test of difference = 0 (vs not =):
T-Value = 4.41 P-Value = 0.000 DF = 16
Both use Pooled StDev = 3.26
10/22/12

7. Problem 1: Data Analysis ... (continued)
MTB > AOVOneway 'STANDAR' 'BARU'.
One-way ANOVA: STANDAR, BARU
Analysis of Variance
Source DF SS MS F P
Factor 1 206.7 206.7 19.48 0.000
Error 16 169.8 10.6
Total 17 376.5
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ----------+---------+---------+------
STANDAR 9 37.222 3.346 (-----*------)
BARU 9 30.444 3.167 (------*------)
----------+---------+---------+------
Pooled StDev = 3.257 31.5 35.0 38.5
10/22/12

8. Problem 2: Simple Comparative Experiments
Manusia, Mesin,
Mobil, Jalan dan
Dua Merk BAN Controllable Factors faktor lain yang dapat
dikontrol dalam kondisi
Ban A Ban B X 1 , X 2 , …, X q TIDAK SAMA
Input Process Output (Y)
Bahan baku Z 1 , Z 2 , …, Z q Jarak tempuh
BAN mobil sampai ban
rusak
Uncontrollable Factors
Apakah ada perbedaan rata-rata jarak tempuh (keawetan) ban
antara ban merk A dan merk B ?
10/22/12

9. Problem 2: Data Eksperimen ... (dalam km)
Ada 5 mobil dengan merk, tahun, rute, sopir,
model dan kondisi mesin yang TIDAK SAMA 
RANDOMIZED BLOCK DESIGN

Ban A
Ban Ban
j
Merk A Merk B Ban B
1. 106 102
2. 98 94
3. 123 118
4. 97 91 
5. 88 83
Posisi ban kiri-kanan kiri-kanan
belakang acak acak
5 mobil
10/22/12

10. Problem 2: Data Analysis ... (continued)
MTB > Paired 'Ban A' 'Ban B'.
 MTB > TwoSample 'Ban A' 'Ban B'; 
SUBC> Pooled.
Paired T-Test and CI: Ban A, Ban B Two-Sample T-Test and CI: Ban A, Ban B
Paired T for Ban A - Ban B Two-sample T for Ban A vs Ban B
N Mean StDev SE Mean
N Mean StDev SE Mean Ban A 5 102.4 13.2 5.9
Ban A 5 102.40 13.16 5.89 Ban B 5 97.6 13.3 5.9
Ban B 5 97.60 13.28 5.94
Difference 4.80 0.837 0.374 Difference = mu Ban A - mu Ban B
Estimate for difference: 4.80
95% CI for mean difference: 95% CI for difference: (-14.48, 24.08)
(3.761, 5.839) T-Test of difference = 0 (vs not =):
T-Value = 0.57 P-Value = 0.582
T-Test of mean diff. = 0 (vs not = 0): DF = 8
Both use Pooled StDev = 13.2
T-Value = 12.83 P-Value = 0.000
difference conclusion !!!
10/22/12

11. Experiments with a Single Factor
People, Machine,
Cotton Weight Method and other
Percentge Controllable Factors controbllable factors are
inthe SAME conditions
X 1 , X 2 , …, X q
15, 20, 25, 30, 35, 40
Input Process Output (Y)
Material Z 1 , Z 2 , …, Z q The tensile
strength
Uncontrollable Factors
Engineer suspects that increasing the cotton content will increase
the tensile strength ?
10/22/12

12. Experimental Run Number
Cotton Weigth
Factor Experimental Run Number
Percentage
25
15 1 2 3 4 5
1
20 6 7 8 9 10
25 11 12 13 14 15
2
30 16 17 18 19 20
35 21 22 23 24 25
Use
computer
Level software
Factor Select a random number between 1 and 25.
A completely randomized design
10/22/12

13. The Test Sequence obtained …
Test Run Cotton Weight Test Run Cotton Weight
sequence Number Percentage sequence Number Percentage
1 8 20 14 7 20
2 18 30 15 1 15
3 10 20 16 24 35
4 23 35 17 21 35
5 17 30 18 11 25
6 5 15 19 2 15
7 14 25 20 13 25
8 6 20 21 22 35
9 15 25 22 16 30
10 20 30 23 25 35
11 9 20 24 19 30
12 4 15 25 3 15
13 12 25
10/22/12

14. Data from the Tensile Strength Experiment …
Cotton Observations
Weight Total Average
1 2 3 4 5
Percent
15 7 7 15 11 9 49 9.8
20 12 17 12 18 18 77 15.4
25 14 18 18 19 19 88 17.6
30 19 25 22 19 23 108 21.6
35 7 10 11 15 11 54 10.8
Total - - - - - 376 15.04
First data 25th data
10/22/12

15. Data Analysis …
Tensile strength (lb/in 2 )
Cotton weight percentage
10/22/12

16. Data Analysis … (continued)
MTB > AOVOneway '15%'-'35%'
One-way ANOVA: 15%, 20%, 25%, 30%, 35%
Analysis of Variance
Source DF SS MS F P
Factor 4 475.76 118.94 14.76 0.000
Error 20 161.20 8.06
Total 24 636.96
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ------+---------+---------+---------+
15% 5 9.800 3.347 (-----*----)
20% 5 15.400 3.130 (----*----)
25% 5 17.600 2.074 (----*----)
30% 5 21.600 2.608 (----*----)
35% 5 10.800 2.864 (-----*----)
------+---------+---------+---------+
Pooled StDev = 2.839 10.0 15.0 20.0 25.0
10/22/12

17. Data Analysis … (continued)
Tukey's pairwise comparisons BERBED
A
Family error rate = 0.0500
Individual error rate = 0.00722 SAMA
Critical value = 4.23
Intervals for (column level mean) - (row level mean)
15 20 25 30
20 -10.971
-0.229
25 -13.171 -7.571
-2.429 3.171
30 -17.171 -11.571 -9.371
-6.429 -0.829 1.371
35 -6.371 -0.771 1.429 5.429
4.371 9.971 12.171 16.171
10/22/12

18. Data Analysis … (continued)
10/22/12

19. Tiga tahap utama dalam Desain Eksperimen
Product and/or
 The Planning Phase process
experts
Product, process
 The Conducting Phase and DOE experts
DOE experts or
 The Analysis Phase statistician
10/22/12