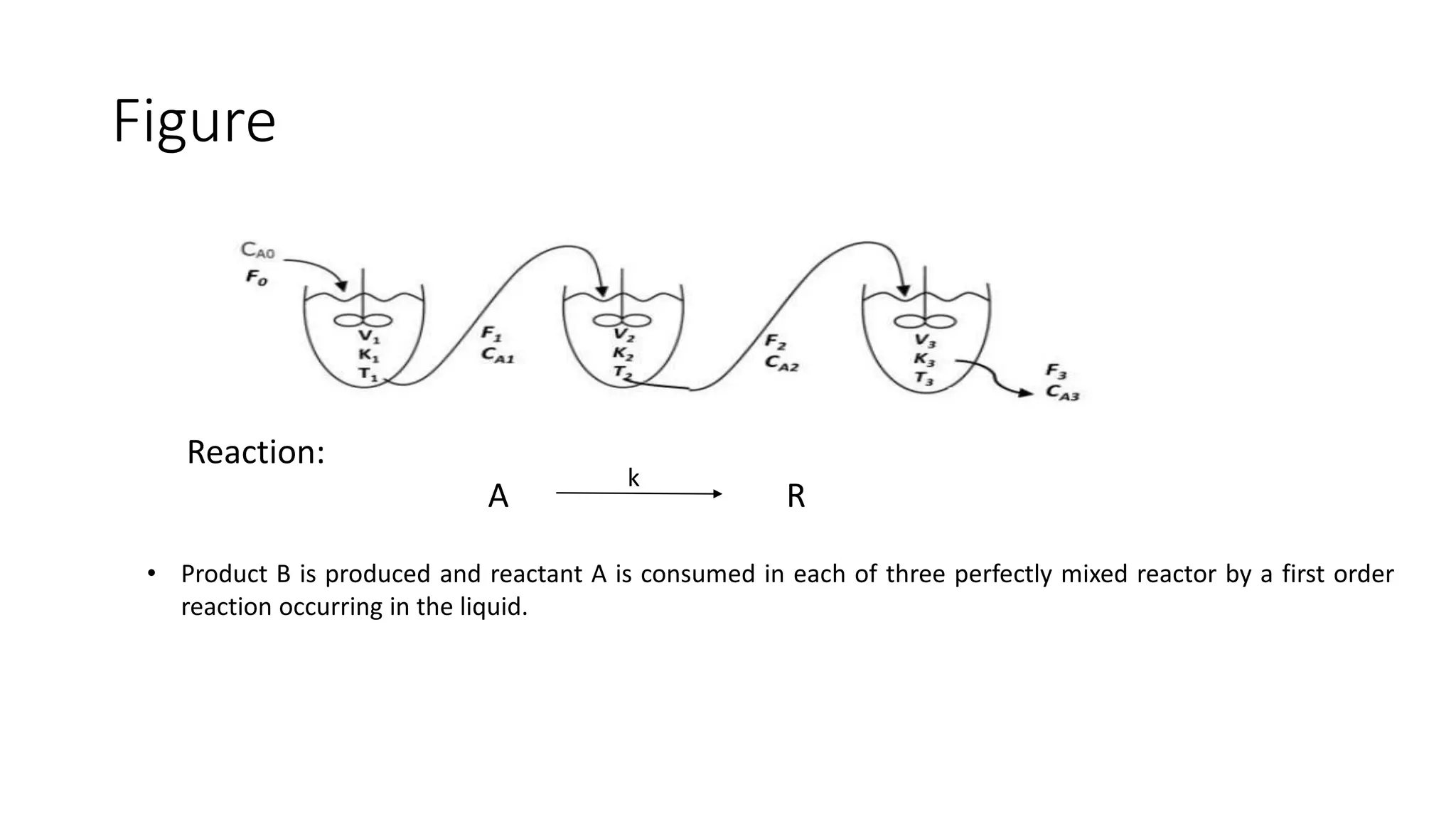
This document presents a mathematical model for a system of three continuously stirred tank reactors (CSTRs) in series where reactant A is converted to product B through a first-order reaction. It describes the assumptions made, including constant temperature, volume, and density in each reactor. Component continuity equations are developed for reactant A in each reactor to model how the concentration of A changes over time based on the inlet and outlet flows and the rate of the reaction. The specific reaction rates are defined using the Arrheusius equation. The model results in a set of three non-linear first-order ordinary differential equations that describe the dynamics of the system.

1. Modeling of constant
holdup CSTR

2. Figure
Reaction:
A R
k
• Product B is produced and reactant A is consumed in each of three perfectly mixed reactor by a first order
reaction occurring in the liquid.

3. Assumption
• The temperature and volume are assumed to be constant.
• Density is remain to be constant through out the system.

4. Cont…
• Now by using the above assumption the formulation of model is
shown below.
• If volume and density of each tank are constant, the total mass is
each tank is constant.
• Thus the total continuity equation for the first reactor is:
𝑑(ρ𝑉1
)
𝑑𝑡
= ρF0 – ρF1 = 0 Eq 1

5. Cont…
• Similarly we can balance for tank 2 and 3 the result we obtain is:
F3 = F2 = F1 = F0 =F
• F is define as throughput (m3/min).
• Now if we want to keep track of the amount of reactant A and
product B in each tank, so component continuity equations are
needed.
• Since the system is binary and we know the total mass of material in
each tank, only one component continuity equation is required.
• If we choose A, the equations describing the dynamic change in
amounts of reactant A in each tank are:

6. Cont…
• V1
𝒅𝑪 𝑨𝟏
𝒅𝒕
= F CA0 −
CA1 − V1K1CA1
• V1
𝒅𝑪 𝑨𝟏
𝒅𝒕
= F CA0 −
CA1 − V1K1CA1
• V1
𝒅𝑪 𝑨𝟏
𝒅𝒕
= F CA0 −
CA1 − V1K1CA1
• Unit of the equations are Kg. mol of A/ min

7. Cont…
• The specific reaction rate Kn are given by Arrhenius equation:
• If the temperature in the reactor are different, the K’s are different.
Kn = αe –E/RT

8. Cont…
• The three first-order non linear ODE gives us mathematical model of
the system.
• The parameters that must be known are V1 ,V2 ,V3,K1, K2, K3.
• The variables that must be specified before these equation can be
solved are F and CA0 .
• The initial condition of the three concentration must be known.

9. Cont…
• Simplify the above ODEs for constant V,T and putting τ = V/F.
• If F is thoughtput, temperature T and holdup V are same in all the
tanks, then τ = V/F(unit is Min).
𝑑𝐶 𝐴1
𝑑𝑡
+ (k + 1/τ) CA1 =
1
τ
CA0
𝑑𝐶 𝐴2
𝑑𝑡
+ (k + 1/τ) CA2 =
1
τ
CA1
𝑑𝐶 𝐴3
𝑑𝑡
+ (k + 1/τ) CA3 =
1
τ
CA2
• In this only Forcing Function is CAO .