deber#9

1. NOMBRE: JOSSELIN YAMBAY CURSO: QUINTO SEMESTRE “A”

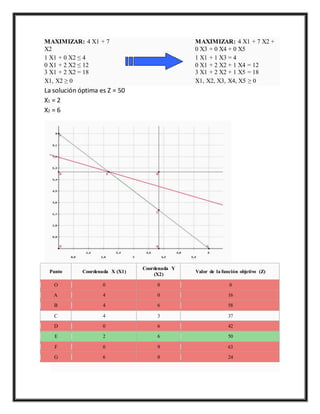
4. MAXIMIZAR: 4 X1 + 7
X2
MAXIMIZAR: 4 X1 + 7 X2 +
0 X3 + 0 X4 + 0 X5
1 X1 + 0 X2 ≤ 4
0 X1 + 2 X2 ≤ 12
3 X1 + 2 X2 = 18
1 X1 + 1 X3 = 4
0 X1 + 2 X2 + 1 X4 = 12
3 X1 + 2 X2 + 1 X5 = 18
X1, X2 ≥ 0 X1, X2, X3, X4, X5 ≥ 0
La solución óptima es Z = 50
X1 = 2
X2 = 6
Punto Coordenada X (X1)
Coordenada Y
(X2)
Valor de la función objetivo (Z)
O 0 0 0
A 4 0 16
B 4 6 58
C 4 3 37
D 0 6 42
E 2 6 50
F 0 9 63
G 6 0 24

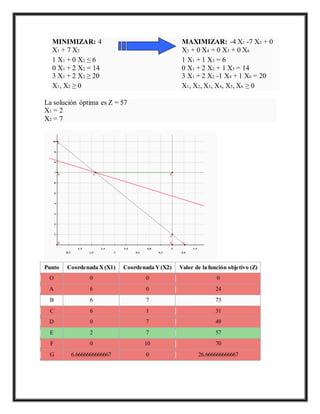
5. MINIMIZAR: 4
X1 + 7 X2
MAXIMIZAR: -4 X1 -7 X2 + 0
X3 + 0 X4 + 0 X5 + 0 X6
1 X1 + 0 X2 ≤ 6
0 X1 + 2 X2 = 14
3 X1 + 2 X2 ≥ 20
1 X1 + 1 X3 = 6
0 X1 + 2 X2 + 1 X5 = 14
3 X1 + 2 X2 -1 X4 + 1 X6 = 20
X1, X2 ≥ 0 X1, X2, X3, X4, X5, X6 ≥ 0
La solución óptima es Z = 57
X1 = 2
X2 = 7
Punto Coordenada X (X1) Coordenada Y (X2) Valor de la función objetivo (Z)
O 0 0 0
A 6 0 24
B 6 7 73
C 6 1 31
D 0 7 49
E 2 7 57
F 0 10 70
G 6.6666666666667 0 26.666666666667

6. MINIMIZAR: 6
X1 + 8 X2 + 16 X3
MAXIMIZAR: -6 X1 -8 X2 -
16 X3 + 0 X4 + 0 X5 + 0 X6 +
0 X7
2 X1 + 1 X2 + 0 X3 ≥ 5
0 X1 + 1 X2 + 2 X3 ≥ 4
2 X1 + 1 X2 -1 X4 + 1 X6 = 5
0 X1 + 1 X2 + 2 X3 -1 X5 + 1
X7 = 4
X1, X2, X3 ≥ 0 X1, X2, X3, X4, X5, X6, X7 ≥ 0
La solución óptima es Z = 35
X1 = 1 / 2
X2 = 4
X3 = 0