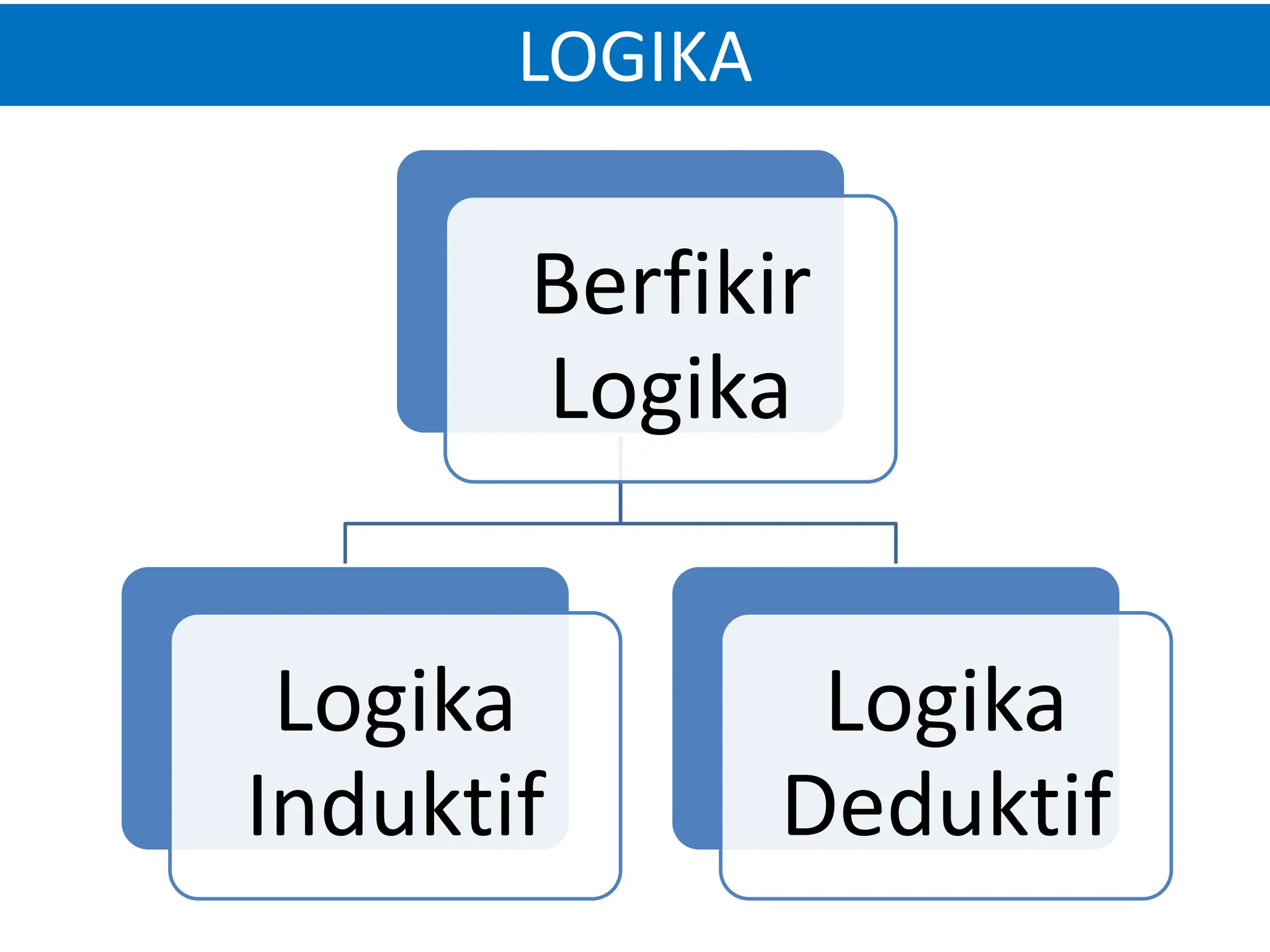
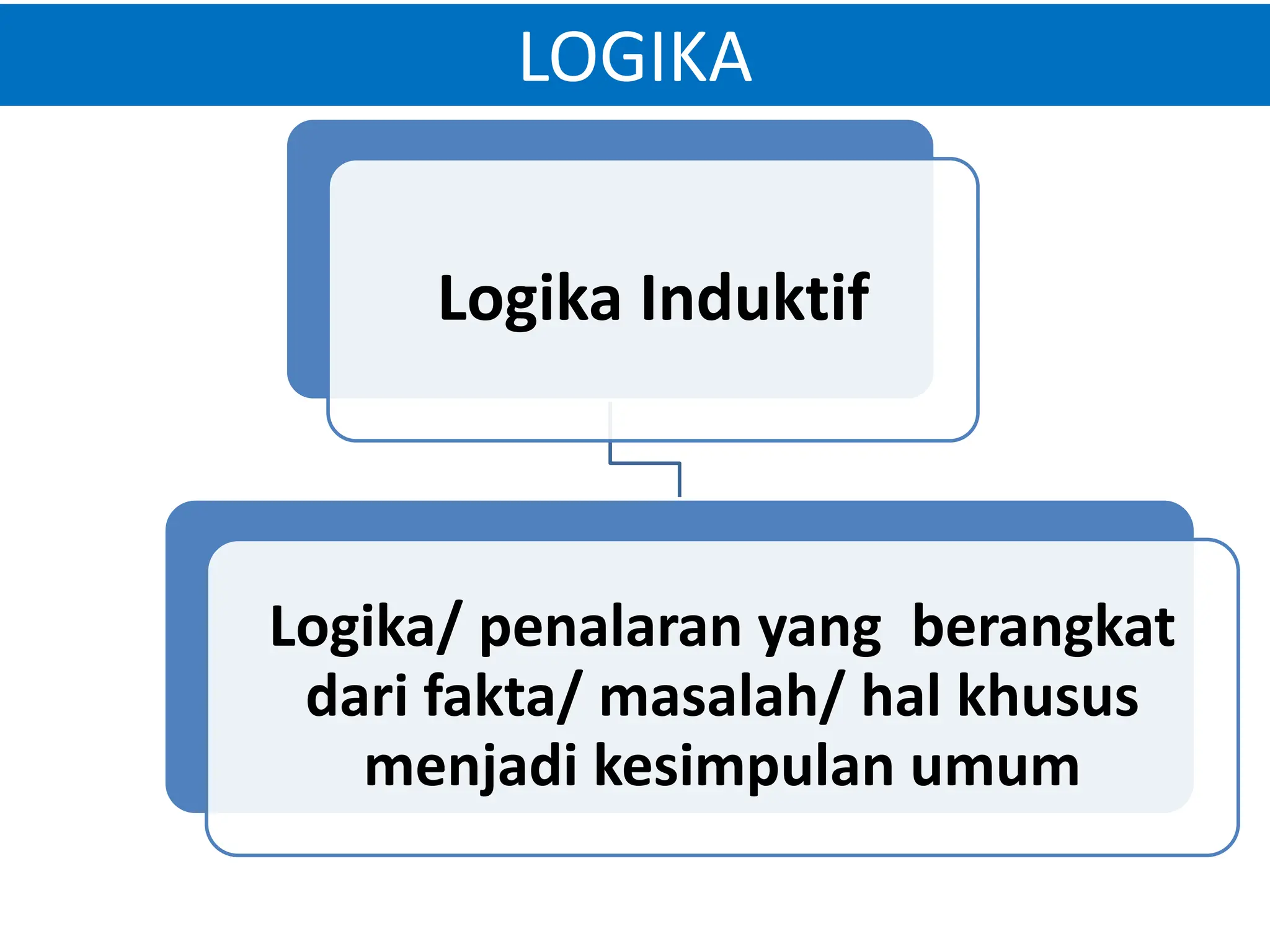
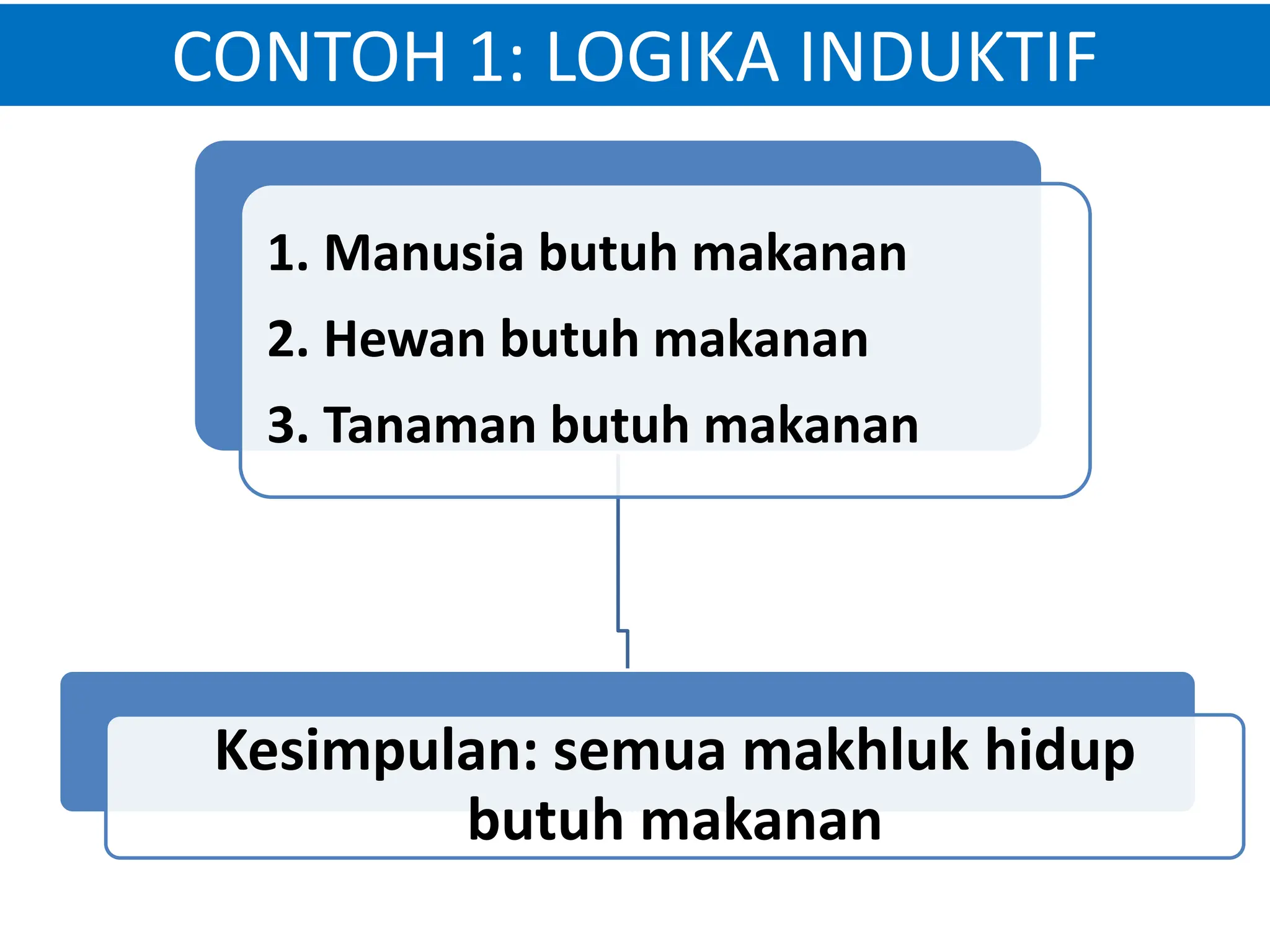
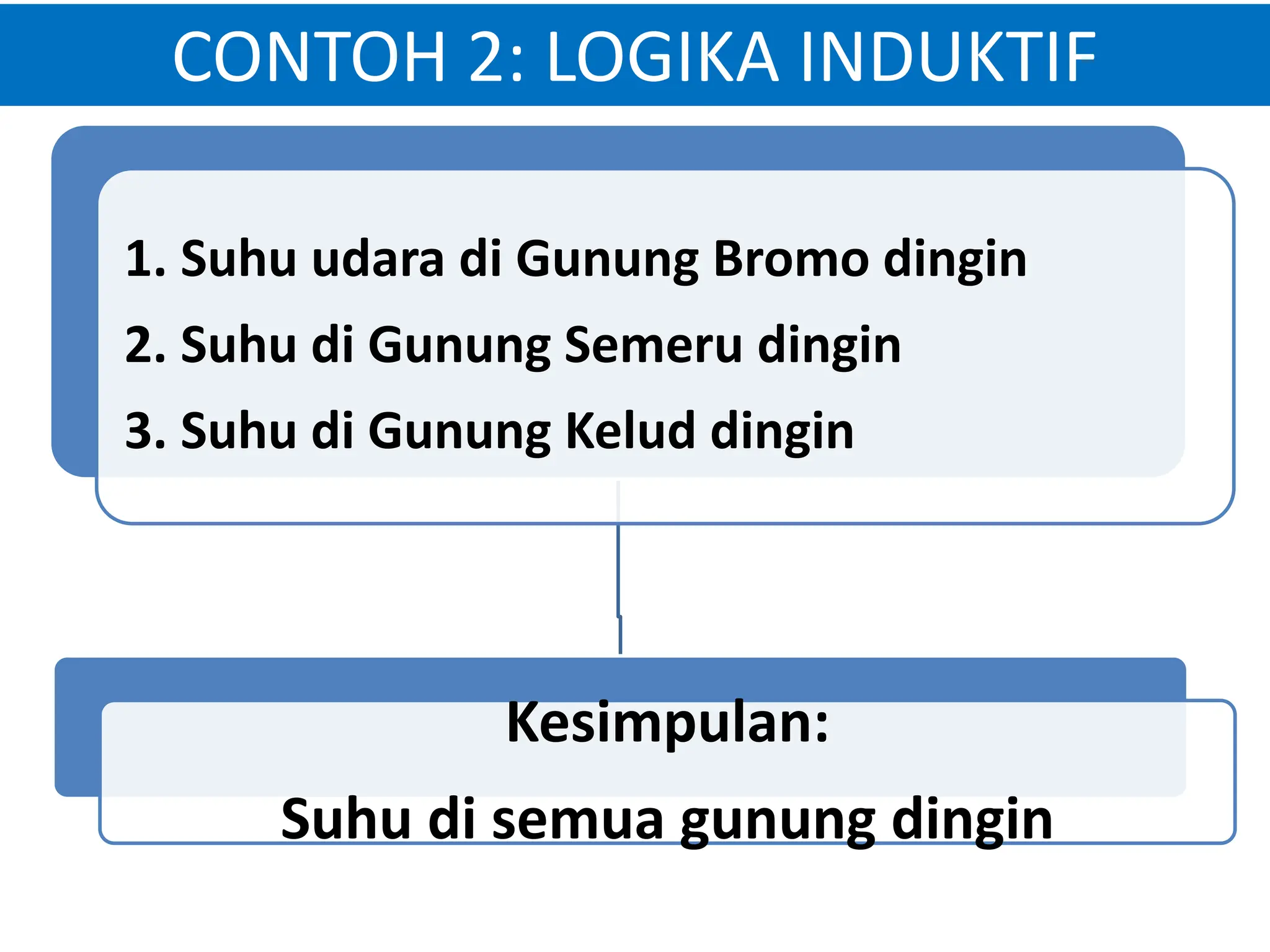
Dokumen tersebut membahas tentang logika, termasuk pengertian logika secara umum sebagai proses berpikir yang membuahkan pengetahuan. Logika dibedakan menjadi logika induktif dan logika deduktif, dengan memberikan contoh untuk masing-masing. Juga dibahas mengenai sumber pengetahuan melalui rasio, pengalaman, intuisi, dan wahyu.

1. Novi Catur Muspita, S. Pd, M.Si
Dosen Fakultas Ilmu Sosial dan Politik UNISBA Blitar
PERNYATAAN & PROPOSISI

2. LOGIKA
proses berpikir yang
membuahkan
pengetahuan.”Agar
pengetahuan yg dihasilkan
penalaran itu mempunyai dasar
kebenaran maka proses berpikir
itu harus dilakukan suatu cara
tertentu.
Suatu penarikan kesimpulan
baru dianggap sahih (valid)
kalau proses penarikan
kesimpulannya

3. LOGIKA
Secara luas logika
diartikan sebagai “
pengkajian untuk
berpikir secara sahih”

4. LOGIKA
Berfikir
Logika
Logika
Induktif
Logika
Deduktif

5. LOGIKA
Logika Induktif
Logika/ penalaran yang berangkat
dari fakta/ masalah/ hal khusus
menjadi kesimpulan umum

6. CONTOH 1: LOGIKA INDUKTIF
1. Manusia butuh makanan
2. Hewan butuh makanan
3. Tanaman butuh makanan
Kesimpulan: semua makhluk hidup
butuh makanan

7. CONTOH 2: LOGIKA INDUKTIF
1. Suhu udara di Gunung Bromo dingin
2. Suhu di Gunung Semeru dingin
3. Suhu di Gunung Kelud dingin
Kesimpulan:
Suhu di semua gunung dingin

8. CONTOH 3: LOGIKA INDUKTIF
1. Motor bergerak memiliki roda
2. Mobil bergerak memiliki roda
3. Sepeda bergerak memiliki roda
Kesimpulan: semua kendaraan yang
bergerak memiliki roda

9. CONTOH 1: LOGIKA DEDUKTIF
1. Semua hewan adalah makhluk hidup
2. Kucing adalah hewan
Kesimpulan: semua kucing adalah
makhluk hidup

10. CONTOH 2: LOGIKA DEDUKTIF
1. Dhila sering olahraga
2. Orang yang rajin berolahraha memiliki
tubuh yang sehat
Kesimpulan: Dhila memiliki tubuh yang
sehat

11. CONTOH 3: LOGIKA DEDUKTIF
1. Wildan suka menulis puisi
2. Orang yang rajin membuat karya puisi
adalah orang yang sering mengalami hati
galau dan resah.
Kesimpulan: …..

12. SUMBER PENGETAHUAN

13. Terdapat 2 cara untuk mendapatkan
pengetahuan yg benar
• Mendasarkan diri pada
rasio
– Kaum rasionalis
– Mempergunakan
metode deduktif
• Mendasarkan diri pada
pengalaman
- kaum empiris
- mempergunakan
metode induktif

14. Masalah yg timbul dari penyusunan
pengetahuan secara empiris
• Pengetahuan yg
dikumpulkan cenerung
untuk menjadi suatu
kumpulan fakta-fakta
• Hakikat pengalaman yg
merupakan cara dalam
menemukan
pengetahuan

15. cara lain untuk mendapatkan pengetahuan yg
benar
• Intuisi. Pengetahuan yg
didapat tanpa melalui
proses tertentu
• Wahyu.merupakan
pengetahuan yg
disampaikan oleh Tuhan
kepada manusia

16. Intuisi
• Bersifat personal dan tidak bisa diramalkan.
Sebagai dasar untuk menyusun pengetahuan
secara teratur maka intuisi ini tidak bisa
diandalkan. Pengetahuan intuitif dapat
dipergunakan sebgai hipotesis bagi analisis
selanjutnya. Kegiatan intuitif dan analitik bisa
bekerja saling membantu dalam menemukan
kebenaran

17. Wahyu
• Pengetahuan ini disalurkan lewat nabi-nabi yg
diutusnya sepanjang zaman. Agama merupakan
pengetahuan bukan saja mengenai kehidupan
sekarang yg terjangkau pengalaman, namun juga
mencakup masalah-masalah yg transedental.
• Kepercayaan kepada Tuhan yang merupakan sumber
pengetahuan, kepercayaan terhadap nabi sebagai
perantara dan kepercayaan terhadap wahyu sebagai
cara penyampaian, merupakan dasar dari penyusunan
pengetahuan ini.

18. 18
Logika (logic)

19. 19
Aristoteles, peletak dasar-dasar logika

20. 20
“Gajah lebih besar daripada tikus.”
Apakah ini sebuah pernyataan? YA
Apakah ini sebuah proposisi? YA
Apakah nilai kebenaran dari
proposisi ini?
BENAR
Permainan

21. 21
“520 < 111”
Apakah ini sebuah pernyataan? YA
Apakah ini sebuah proposisi? YA
Apakah nilai kebenaran dari
proposisi ini?
SALAH
Permainan

22. 22
“y > 5”
Nilai kebenaran dari pernyataan tersebut
bergantung pada y, tapi nilainya belum
ditentukan.
Pernyataan jenis ini kita sebut sebagai fungsi
proposisi atau kalimat terbuka.
Apakah ini sebuah pernyataan? YA
Apakah ini sebuah proposisi? TIDAK
Permainan

23. 23
“Tolong untuk tidak tidur selama kuliah”
TIDAK
TIDAK
Hanya pernyataanlah yang bisa menjadi
proposisi.
Ini adalah sebuah permintaan.
Apakah ini sebuah pernyataan?
Apakah ini sebuah proposisi?
Permainan

24. 24
Contoh 1. Semua pernyataan di bawah ini adalah
proposisi:
(a) 13 adalah bilangan ganjil
(b) Soekarno adalah alumnus UGM.
(c) 1 + 1 = 2
(d) 8  akar kuadrat dari 8 + 8
(e) Ada monyet di bulan
(f) Hari ini adalah hari Rabu
(g) Untuk sembarang bilangan bulat n  0, maka
2n adalah bilangan genap
(h) x + y = y + x untuk setiap x dan y bilangan
riil 

25. 25
Contoh 2. Semua pernyataan di bawah ini bukan
proposisi
(a) Jam berapa kereta api Argo Bromo tiba
di Gambir?
(b) Isilah gelas tersebut dengan air!
(c) x + 3 = 8
(d) x > 3 
Kesimpulan: Proposisi adalah kalimat berita

26. 26
• Kembali ke kalkulus proposisi
• Proposisi dilambangkan dengan huruf kecil p, q, r,
….
• Contoh:
p : 13 adalah bilangan ganjil.
q : Soekarno adalah alumnus UGM.
r : 2 + 2 = 4

27. TERIMA KASIH ATAS
PERHATIANNYA
SALAM SEHAT & SEMANGAT