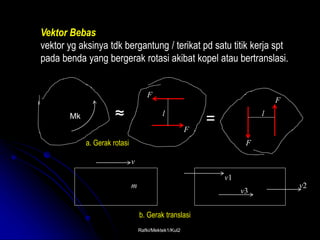
Dokumen tersebut membahas konsep dasar statika yang mencakup (1) definisi mekanika struktur dan jenis-jenisnya, (2) hukum-hukum dasar Newton, (3) satuan-satuan yang digunakan dalam statika, (4) vektor dan jenis-jenis vektor, (5) konsep gaya dan jenis-jenis gaya, serta (6) penjumlahan dan penguraian gaya.

1. Rafki Imani
Fakultas Teknik
Universitas Putra Indonesia
STATIKA
Engineering Mechanics
Yayasan Perguruan Tinggi Komputer Padang

2. Rafki/Mektek1/Kul2
KONSEP DASAR
STATIKA
Mekanika / Statika Struktur:
Ilmu yg mempelajari & meramalkan kondisi benda diam /
bergerak akibat pengaruh gaya yg bereaksi pd benda tsb
Dibedakan:
1. Mekanika benda tegar (mechanics of rigid bodies)
2. Mekanika benda berubah bentuk (mechanics of deformable)
3. Mekanika fluida (mechanics of fluids)

3. Rafki/Mektek1/Kul2
Mechanics
Dynamics
Statics
Deformable Bodies Fluids
Rigid Bodies
Compressible
Imcompressible

4. Mekanika benda tegar:
 Statika : mempelajari benda dlm keadaan diam
 Dinamika : mempelajari benda bergerak
Pada benda tegar, tdk pernah benar2 tegar melainkan tetap mengalami
deformasi akibat beban yg diterima, tapi umumnya deformasinya kecil,
shgg tdk mempengaruhi kondisi keseimbangan / gerakan struktur
yg ditinjau maka diabaikan
Fokus Mekanika Teknik (1): Mempelajari benda tegar dlm
keadaan diam
Rafki/Mektek1/Kul2

5. Dasar Hukum Statika
Hukum Newton I
ΣFx= 0
ΣFy= 0
ΣM = 0
Hukum Newton II
F = m.a = kg.m / dt = N
Hukum Newton III
Aksi = Reaksi
2
dt
2
Rafki/Mektek1/Kul2

6. Satuan
Mekanika berkaitan dengan 4 Besaran Dasar: Panjang, Massa, Gaya
dan Waktu. Lambang dari besaran2 tsb dinamakan dengan Satuan.
Sistem satuan:
1. Sistem Satuan Internasional (SI)
2. Sistem Satuan British
Jenis Satuan:
1. Satuan Pokok: satuan dasar yg tdk bergantung dg satuan lainnya,
misal:
a. Massa ( m ): satuannya kilogram (kg) atau gram (g)
b. Waktu ( t ) : satuannya detik ( dt )
c. Panjang ( l ): satuannya meter (m), centimeter (cm),
atau milimeter (mm)
Rafki/Mektek1/Kul2

7. 2. Satuan Turunan: satuan yg diperoleh dr satuan pokok.
Contoh:
a. Kecepatan ( v ) : turunannya: panjang/waktu = m / s
b. Percepatan ( a ): turunannya: kecepatan / waktu = m / s2
Rafki/Mektek1/Kul2

8. Dalam statika, satuan yg paling sering dipakai
adalah satuan yg mengacu pada sistem Satuan
Internasional
Besaran Simbol
Kecepatan, v m/s
Gaya, F N
Percepatan, a m/s^2
Momen,M Nm atau Nmm
Massa, m Kg
Panjang, l m atau mm
Daya, W W
Tekanan, P N/m^2 atau Pascal (Pa)
Tegangan, σ, τ N/mm^2 atau MPa
dll
Rafki/Mektek1/Kul2

9. Rafki/Mektek1/Kul2
Simbol Satuan

10. Vektor
Dalam mekanika, ada dua besaran:
1. Besaran skalar: Besaran yg hanya mempunyai nilai (harga) –nya saja.
Contoh: massa, panjang, volume, waktu, energi, dll.
2. Besaran vektor: Besaran yang mpy nilai dan arah.
Contoh: momen, kecepatan, percepatan, gaya, dll.
Macam2 vektor:
1. Vektor bebas
2. Vektor tetap / tertentu / terikat
3. Vektor geser
Rafki/Mektek1/Kul2

11. Vektor Bebas
vektor yg aksinya tdk bergantung / terikat pd satu titik kerja spt
pada benda yang bergerak rotasi akibat kopel atau bertranslasi.
Mk ≈ =
l
F
F
F
F
l
v
m
v1
v3
v2
a. Gerak rotasi
b. Gerak translasi
Rafki/Mektek1/Kul2

12. Vektor Tetap
adlh vektor yg mpy titik kerja yg harus dipertahankan. Apabila titik kerja
tsb mengalami perubahan, maka akan diperoleh perubahan akibat
pengaruh thdp benda tsb.
Benda yang diberikan aksi vektor
Rafki/Mektek1/Kul2

13. Vektor Geser
adlh vektor yg dlm aksinya harus mempertahankan garis kerja.
Aksi suatu vektor yg mempertahankan garis kerja
Rafki/Mektek1/Kul2

14. Rafki/Mektek1/Kul2
2. Konsep Gaya
Sistem Gaya
 Gaya adalah aksi sbh benda thdp benda lain yg umumnya ditentukan
oleh titik tangkap (titik kerja), besar dan arah, yg mrp sbh besaran vektor
 Sbh gaya mpy besar, arah & titik kerja tertentu yg digambarkan dgn
anak panah. Besarnya sebanding dgn pnjg anak panahnya.
 Satuan Gaya:
SI Units: N (Newton)
kN (kilo Newton = 1000 N)
US Units:
Pounds (lb); kip (k) = 1000 lb
F
Besar
Titik kerja/garis kerja gaya
arah

15. Rafki/Mektek1/Kul2
Jenis Gaya
1. Gaya Kolinier: gaya2 yg garis kerjanya berada pd satu grs lurus
2. Gaya konkuren: gaya2 yg garis kerjanya berpotongan pd satu titik
3. Gaya Kopel: sepasang gaya yg sejajar sama besar & berlawanan arah
yg bekerja pd suatu batang (benda), dmn akan menimbulkan momen (kopel)
pd batang tersebut.
M = F x r ; dengan F adalah gaya dan r adalah jarak antar gaya=kN.m
F3
F2
F1
F3
F1 F2
F4
OF
r
F
F

16. Rafki/Mektek1/Kul2
Yaitu garis yg panjangnya tak
tertentu yg terdpt pd vektor gaya
tsb.
Titik tangkap suatu gaya dpt
dipindahkan ke titik lain yg terletak
pd garis kerjanya, tanpa mengubah
efek translasional dan rotasional dr
gaya thdp benda yg dibebani.
Gaya yg bekerja pd benda tegar dpt
dipandang bekerja dimana saja di
sepanjang garis kerjanya
Garis Kerja Gaya

17. Rafki/Mektek1/Kul2
a. Gaya kolinier
b. Gaya konkuren

18. Rafki/Mektek1/Kul2
Sistem Gaya Space (3D)

19. Rafki/Mektek1/Kul2
3. Resultan/Penjumlahan Gaya
Definition:
Two forces acting or more on a particle/structure can be replaced by a single
force, called Resultant.
Dlm penyelesaian masalah vektor Resultan 2 gaya dpt ditentukan dgn metode
Grafis dan Analitis.
Metode Grafis:
1. Metode Jajaran Genjang
2. Metode Segitiga
Metode Analitis/aljabar:
1. Metode Sinus-Cosinus
2. Metode proyeksi ke sumbu yg saling tegak-lurus

20. Rafki/Mektek1/Kul2
1. Metode Grafis Jajaran Genjang (disebut juga: Paralelogram Law)
2. Metode Grafis Segitiga
A
F2
F1
A
F2
F1
R
A
F2
F1
R

21. Rafki/Mektek1/Kul2
Resultan Beberapa Gaya (Lebih dari 2 gaya)
Misalkan sbh benda mendapat aksi gaya sbb:
F2
F5
F1
F3
F4
1. Metode Paralelogram:
F2
F5
F1
F3
F4
R1
R2
R3
R
2. Metode Poligon:
R

22. Rafki/Mektek1/Kul2
Metode Analitis/Aljabar:
Aturan Segitiga/Aturan Sinus-Cosinus
A
B
C
β α
γ


 sin
sin
sin
C
B
A



cos
2
2
2
AB
B
A
C 



23. Rafki/Mektek1/Kul2
Contoh Soal:
Tentukan Resultan dari gaya2 yg bekerja pd benda di bawah!

24. Menentukan komponen gaya secara grafis
Rafki/Mektek1/Kul2

25. Rafki/Mektek1/Kul2
Komponen/Penguraian Gaya
Gaya dpt diuraikan mjd komponen vertikal dan horizontal atau mengikuti
arah sumbu -x dan –y
F
Fy
Fx
x
y
θ
θ : sudut kemiringan gaya
Fx : F cos θ
Fy : F sin θ
F
Fx
F
Fy

 
 cos
;
sin
Fx
Fy


tan
2
2
y
x F
F
F 

Jika terdpt bbrp gaya yg mpy komponen x dan y, maka Resultan gaya dpt dicari dg
menjumlahkan gaya2 dlm komponen x dan y:
y
y
x
x F
R
F
R 


 ;
Fx adalah gaya horizontal (sejajar sumbu –x)
Fy adalah gaya vertikal (sejajar sumbu –y)

26. Rafki/Mektek1/Kul2