The document provides an overview of matrices, defining them as rectangular arrays of elements organized in rows and columns, and explains different types, including row, column, null, square, diagonal, unit, and triangular matrices. It details the properties of these matrix types, such as the conditions that define them. The content serves as an introduction to the fundamental concepts of matrices and their classifications.

1. Matrix
LEVEL -2
NANDHITHA.K
23- EDM-12

2. MATRIX
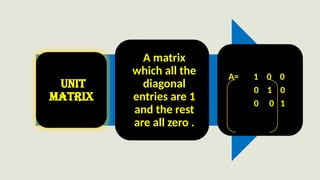
A Matrix is a rectangular array or arrangement of entries or
elements displayed in rows and columns put within a square
bracket [ ].
Matrices are denoted by capital letters A, B, C, ... etc.
 If a matrix A has m rows and n columns, then it is written as,
 ,1  i  m, 1 j  n.

3. In a matrix, the horizontal lines of elements are known as Rows
and the vertical lines of elements are known as Columns.

Row 1
Row 2
Row n
Row m
m rows

4. Types of Matrices
Row matrix
A matrix
having only
one row
column
matrix
A matrix
having only
one column
null matrix
A matrix is said to be
a zero matrix or null
matrix or void matrix
denoted by O. If aij=0
for all values.

5. EXAMPLES
Row matrix
A = []
2×1
Column matrix
A =
2×2
Null matrix

6. SQUARE MATRIX
 A matrix in which number of rows is equal to the number of
columns, is called a Square matrix.
 That is, a matrix of order n × n is often referred to as a square
matrix of order n.
 A = is a square matrix of order 3.

7. diagonal matrix
A square matrix is called a
Diagonal matrix if aij=0
whenever i≠j.
𝟏 𝟎 𝟎
𝟎 𝟐 𝟎
𝟎 𝟎 𝟑
𝐴=¿

8. UNIT
MATRIX
A matrix
which all the
diagonal
entries are 1
and the rest
are all zero .
A= 1 0 0
0 1 0
0 0 1

9. triangular matrix

10. triangular matrix
A Square Matrix is said to be a
Upper Triangular matrix if all the
elements below the main
diagonals are zero.
UPPER
TRIANGULAR
MATRIX
A Square matrix is said to be a
lower triangular matrix if all the
elements above the main
diagonals are zero.
LOWER
TRIANGULAR
MATRIX

11. THANK YOU

12. Click icon to add picture