1. Tennis StatisticsTennis Statistics
A Better Ranking System &A Better Ranking System &
An In-Play Probability AnalysisAn In-Play Probability Analysis
Peter SchindlerPeter Schindler
Imperial College LondonImperial College London
MSc ThesisMSc Thesis
August 28, 2015August 28, 2015
2. Acknowledgements
Firstly, I would like to express my gratitude to my supervisor Dr. Daniel Mortlock for his
excellent guidance and flexible attitude. I feel extremely lucky to have worked with someone as
passionate about tennis as I am.
Secondly, a huge thank you goes to my good friend Andrei Cioara, who helped me with the
web scraping of the point-by-point data. Without him, important parts of this project would
not have been possible.
Last but not least, I would like to say a big thank you to my mother Marianna and brother
Adam. They have always been there for me throughout my life, during the highs and lows, and
have permanently provided me with the best of their love and support.
3. Details
Name: Peter Schindler
CID Number: 00694136
Name of Supervisor: Dr Daniel Mortlock
Email Address: peter.schindler11@imperial.ac.uk
or schindlerpeter@ymail.com
Home Address: 7 Rue Saint Honore, Versailles, 78000, France
Plagiarism Statement
This is my own unaided work unless stated otherwise.
4. Abstract
The current ATP ranking system is far from perfect. Firstly, we develop an alternative way of
ranking tennis players using the Elo rating methodology. We then compare the rankings given
by our Elo model to the current official rankings. In a second part, we develop a tool to analyse
in-play tennis matches. This tool will enable the tracking of the match-outcome probability on
a point-by-point basis, as well as the identification of the important points in the match. We
illustrate its performance by applying it to the 2014 Wimbledon final between Roger Federer
and Novak Djokovic.
6. 1 Introduction
On June the 9th 2013, the French Open final was set to be an all Spanish affair between world
number 4, the king of clay Rafael Nadal, and world number 5 David Ferrer. Two days earlier,
Nadal emerged victorious from a titanic five-hour battle against world number 1 Novak Djokovic,
whereas Ferrer’s route to the final was relatively calm. In the final, Nadal was clearly the better
player and ruthlessly dispatched his compatriot 6:3 6:2 6:3. The next day however, when the official
ATP rankings were updated, Ferrer ascended to world number 4, overtaking Nadal, who now was
ranked 5. One might be thinking: ”Wait, that cannot be right! Surely there must be something
wrong with this ranking system!”.
The Association of Tennis Professionals (ATP) is the governing body of men’s professional
tennis. Every year, there are 66 ATP tournaments organised across the globe, where the world’s
elite tennis players participate in order to collect ATP ranking points. The points gathered by a
player in the past 52 weeks are then summed up to give his total ranking points. Arranging all the
players’ total points in decreasing order then gives rise to the official ATP World Tour rankings 1.
As pointed out to in the opening paragraph, the ATP ranking system is far from perfect. In
fact, mathematically speaking, it is pretty average. In the first part of this thesis, we will look
into an alternative way of building a ranking system for tennis players. This method is commonly
known as the Elo rating system, and it will be studied in great depth in Section 3. Firstly, the
fundamentals will be presented in Section 3.1, and then an extension of these basics will be discussed
in Section 3.2. Alongside the theory and the algorithms, the rankings obtained by this Elo model
will be displayed in these sections. These Elo ratings do not only enable the ranking of players, but
they can be used to estimate match-outcome probabilities, so we will also include an explanation
of how this is done. To wrap up Section 3, a comparative analysis is conducted between the official
ATP and our Elo rankings. We reveal which one is the better ranking system and will give solid
arguments to back our claim.
The second part of this thesis has a slightly different feel to it than the first one, as its final
goal is entirely different. In this Section 4, we aim to conduct an in-depth probability analysis of
a tennis match on a point-by-point level. The inspiration for this work came from a sports betting
tool called Tennis Trader2, part of the Bet Angel betting software. Tennis Trader is a computer
program built to facilitate the tennis betting of professional sports traders on Betfair3. It is an
in-play profiling tool, allowing traders to get an idea of the direction the odds might be heading.
Our focus however, will not be on odds but rather on probabilities, more specifically the match-
win probability of the players of a given match. In Sections 4.1 and 4.2, a thorough explanation
will be given of the ingredients required to obtain these desired match-win probabilities. The cherry
on the cake will come in Section 4.3, where we will take the example of the 2014 Wimbledon final
between Novak Djokovic and Roger Federer, and conduct a full point-by-point analysis on it. The
evolution of Djokovic’s match-win probability (i.e. 1 - Federer’s match-win probability) will be
presented in Section 4.3.1 and the important points of the match will be flagged out in Section
4.3.2. This thesis is wrapped up with some concluding thoughts and remarks in Section 5.
1
For a more detailed account on how this ranking system works, please see division 7.2 of the Appendix.
2
For a detailed account about the in-and-outs of Tennis Trader, please consult www.betangel.com/tennis/.
3
Betfair is the worlds largest Internet betting exchange platform, counting over 4 million customers worldwide.
1
7. In order to fully appreciate the content of this thesis, knowledge of the tennis scoring system is
strongly recommended. For those not entirely familiar with it, a detailed explanation is included in
division 7.1 of the Appendix.
Before we dive into this world of tennis statistics, let us describe the datasets that we will work
with.
2
8. 2 The Data
In this thesis we will mainly work with two datasets. The first dataset is a larger and more general
one, whereas the second one is smaller, but contains more detailed information.
2.1 Match Result Data
We take the data needed for our first dataset from the www.tennis-data.co.uk/alldata.php website.
This data describes the results of singles tennis matches of the ATP World Tour from the 1st
of January 2000 up until matches on the 1st of August 2015. After having applied some basic
transformations to this raw data, we end up with a dataset containing 43,317 rows and 23 columns.
We call this dataset tennis1. Each row of tennis1 corresponds to one match and it has the following
columns:
1. Winner - Name of the player who won the match.
2. Loser - Name of the player who lost the match.
3. WRank - ATP ranking of the winner.
4. LRank - ATP ranking of the loser.
5. nSet - Maximum number of sets allowed in the match: 3 or 5.
6. Wsets - Number of sets won by the winner.
7. Lsets - Number of sets won by the loser.
8. Surface - Surface the match is played on: hard, clay or grass.
9. Date - Date of the match.
10. nWplay - Number of matches the winner has played in the dataset previous to the current
match.
11. nLplay - Number of matches the loser has played in the dataset previous to the current match.
12. Comment - The completion status of the match: either the match was Completed or the loser
Retired. Note: Walkover (victory without play) matches are excluded from the dataset.
It is also important to note that tennis1 is arranged by date: it starts with the first matches of the
year 2000 and ends with the last matches of 2015. The significance of this chronological ordering
will become clear in Section 3.
2.2 Point-by-Point Data
In tennis, the final result of a match does not contain any information on how this final score came
about. In what order were the points won? When did the breaks happen? Who won the key points
of the match? etc. A point-by-point dataset, containing the sequence of points for every match
would give answers to all these questions. However, the problem is that such data is very hard to
find and even harder to acquire.
3
9. To our great delight, the website www.flashscore.com/tennis/ recently introduced point-by-point
data for every ATP World Tour match from 2014 onwards. Therefore writing a web scraper4 in
order to extract this data from the website seemed to be the solution. However, the big problem was
that this flashscore website was JavaScript intensive, and instead of getting the point-by-point data
on a HTML directly, it was getting it through asynchronous JavaScript AJAX calls. This made the
process significantly harder, because the execution of the JavaScript in the context of the page was
required. Two options were available to us: either reverse engineer the website to find the HTTP
endpoints that the page was calling for the actual scores, or simply execute the JavaScript code
ourselves. We decided to go for the latter, because it was faster to implement for a prototype. In
order to achieve this, we used a NodeJS (JavaScript) library called PhantomJS. This is a headless
browser that integrates nicely with the NodeJS environment. We used it to load and execute the
page we needed in order to receive all the matches. After having received the correct page, we
parsed its content using the CheerioJS library and created a JSON file. To finish, we fed this into
our R program, obtaining the desired data in a more friendly and usable format.
Having the point-by-point data for all ATP World Tour singles matches (roughly 4,110 matches)
between the 1st of January 2014 and the 1st of August 2015, opened up a wide range of possibilities.
In Section 4.3, it will allow us to plot point-by-point probability evolution of match outcomes, but
first we will make use of this data in Section 4.1. In Section 4.1, our interest will lie in estimating
the point-win probability of the player on-serve. Henceforth, we assume the fraction of service
points won by a player in a match to be a good estimator of the true value of his on-serve point-win
probability for that match. So, for each of the 4,110 matches, we can compute the percentage of
service points won by both the winner and the loser player.
The matches for which we have point-by-point data are equally found at the end of the tennis1
dataset, so our second dataset will be these 4,110 matches (rows) from tennis1 with the addition
of the following two columns to the existing twelve:
13. pW - Fraction of on-serve points won by the winner of the match.
14. pL - Fraction of on-serve points won percentage of the loser of the match.
We call this dataset tennis2. It will be extensively used in Section 4.1.
4
This web scraper was written with huge contribution of my friend and computer scientist Andrei Ioan Cioara.
4
10. 3 The Elo Rating System
Sport performance cannot be measured absolutely; it has to be inferred from wins and losses against
other competitors. A competitor’s level depends on his results against his opponents and their levels.
The levels of competitors can be quantitatively summarized by a rating system.
The Elo rating system is a method for calculating the relative skill levels of players in competitor-
versus-competitor games. It is named after its creator, the Hungarian physicist ´Arp´ad ´El˝o (1903-
1992). As presented in the original works Elo (1961) and Elo (1978), the system was invented in
order to serve as an improved chess rating system. Since then, its popularity has expanded, and
today its usage can be found in a wide variety of other competition games. Even Mark Zuckerberg
employed a version of the Elo rating system when building Facebook’s predecessor called Facemash;
a website that ranked Harvard students based on their levels of attractiveness!
In professional sports, Elo rating systems are also present, but are rarely endorsed by the sports’
governing bodies. The only Elo-based rankings used by a sport’s governance are for FIFA Women’s
Football. A good explanation of how these football Elo rating systems work can be found in Bhulai
and Szl´avik (2012).
In this section, we will be interested in applying the Elo rating system in the context of tennis.
Firstly, the underlying methodology will be explained, and then we will use the system to rank
professional men tennis players. We will also illustrate how the Elo model can be used to obtain
match-outcome probabilities. Works of the similar flavour have also been conducted in Clarke et al.
(1994) and Clarke and Dyte (2000).
3.1 Basics of the Elo
The fundamental assumption behind the Elo theory is that in any competitor-versus-competitor
game, a competitor’s skill level can be summarised by a single statistic, called an Elo rating. In
fact, the key idea driving this method is that the rating difference between two competitors can
give rise to a prediction of the outcome of the encounter.
3.1.1 The Elo Function
The function allowing this transition from competitors’ ratings to the probability of the outcome,
is the well-known logistic function, given by:
f(x) =
m
1 + e−α(x−x0)
, (1)
where m is the function’s maximal value, x0 is the x-value of the sigmoid’s midpoint and α is a
scaling parameter that tunes the steepness of the logistic curve. This function is of ideal use in an
Elo set-up. Let R1 denote the rating of Player 1 and R2 that of Player 2. Then setting m = 1,
x = R1 and x0 = R2, the logistic function will consequently output a value between 0 and 1, which
can therefore naturally be treated as a probability. So we define the Elo function ξ to be:
ξ(R1, R2) :=
1
1 + e−α(R1−R2)
, (2)
for a pre-specified α. Note that the parameter α solely has scaling purposes and hence the resulting
probability only depends on the difference R1 − R2.
5
11. Suppose π := ξ(R1, R2) represents the probability that Player 1 wins the match against Player
2. The following plot shows the Elo function for the value α = 1/2000:
Figure 1: The curve Elo function for α = 1/2000
Looking at this graph, we make the following type of statements:
1. If R1 − R2 = 0, meaning that the two players have the same level (i.e. R1 = R2), the Elo
function estimates probability π of Player 1 winning against Player 2 to be π = 0.5.
2. If say R1 −R2 ≈ 500, meaning that Player 1 is a slight favourite (i.e. R1 > R2), then π ≈ 0.56.
3. If say R1 −R2 ≈ −5000, meaning that Player 2 is the overwhelming favourite (i.e. R1 << R2),
then π ≈ 0.08.
As all this makes not just mathematically, but also common sense, it becomes clear why the Elo
function is so appropriate. Therefore let us move on to showing how this function is employed to
construct an algorithm.
3.1.2 The Basic Elo Algorithm
Elo ratings are the result of a sequential algorithm called the Elo algorithm (or model). The basic
version of this algorithm is very simple and works surprisingly well in practice. It contains one
6
12. for-loop and has only a single parameter. For our tennis1 dataset and the MSE 5 as error measure,
the algorithm is as follows:
Algorithm 1 BASIC ELO
1: Fix parameter k
2: Let mse := 0
3: Let M be the number of players in the dataset.
4: Initialise ratings by setting Rm := 1000 for m in 1 → M
5: Let N be the number of matches in the dataset.
6: for i in 1 → N do
7: Compute the probability π(i) := ξ(R
(i)
W , R
(i)
L ) of the winner winning match i, where R
(i)
W and
R
(i)
L are the ratings of the winner and loser of match i respectively
8: Let π∗(i) denote the observed probability of the winner winning match i. Clearly π∗(i) = 1.
9: mse := mse + (π∗(i) − π(i))2
10: R
(i)
W := R
(i)
W + k × (π∗(i) − π(i))
11: R
(i)
L := R
(i)
L − k × (π∗(i) − π(i))
12: end for
13: Finalise MSE := mse/N
Let us comment on this algorithm6. Firstly, the setting of all initial ratings to the arbitrary
number of 1000 (line 4) is simply for visual convenience. Secondly, it is crucial to point out, that the
magnitude of the rating updates (lines 10-11) plays a vital role in the success of the algorithm. The
rating of the winner is increased by an amount that depends on his chance of winning: the amount
is small if the chance of winning is high and vice versa. In a tennis match, a player can either be
the favourite (probability of winning > 0.5) or the underdog (probability of winning < 0.5), and
as the two only possible outcomes of a match are winning or losing, this gives rise to two possible
scenarios:
1. Favourite Wins - an expected victory, hence |π∗(i) − π(i)| will be small and so the win will
increase the favourite’s rating by a small amount
Underdog Loses - an anticipated defeat, hence |π∗(i) − π(i)| will be small and so this loss will
decrease the underdog’s rating by a small amount
2. Underdog Wins - a surprise victory, hence |π∗(i) −π(i)| will be big and so this win will increase
the underdog’s rating by a big amount
Favourite Loses - an unexpected defeat, hence |π∗(i) − π(i)| will be big and so this loss will
decrease the favourite’s rating by a big amount
5
Explained in the next section
6
The R code implementing this algorithm can be found in Section 7.6.
7
13. The following table helps with the visualisation:
Table 1: Simple visualisation of the main idea underlying the Elo algorithm. Arrows indicate the magnitude
and direction of the rating update after a match.
It should be noted that the usage of the words ”big” and ”small amount” are quite vague. The
magnitude of the increase or decrease of the ratings are controlled by the parameter k. But for
what value of k do we get optimal model performance?
3.1.3 Tuning the Elo
In order for an Elo algorithm to work and give satisfying results, it has to be tuned correctly.
Tuning here means finding the set of parameter values that minimize the error measure. There are
a multitude of error measures at our disposition that we could make use of. There is no wrong or
correct choice, as each measure has its advantages and limitations. We could choose to go for the
Likelihood or the Mean Absolute Deviation, but in order to be more punishing on the larger errors
made by the model, we opt for a well-established error measure called the Mean Squared Error
(MSE) 7. Its formula is given by:
MSE =
1
N
N
i=1
(π∗(i)
− π(i)
)2
, (3)
where the notation used is the same as encountered in Algorithm 1. We shall stick with this error
measure for the remainder of this thesis.
The basic rule of thumb for the MSE, is that lower its value, the better the model. A tuned
model is one where no other set of parameters gives a lower MSE than the MSE given by the current
set of parameters. For a given Elo algorithm, we an optimiser function 8 is used in order to finding
an optimal (satisfactory but not perfect) set of parameters of the algorithm. Applying this opti-
miser to Algorithm 1, we find k = 300.9 to be optimal with an error measure of MSE = 21.36×10−2.
3.1.4 Burn-In Period
Before we move on to building a more voluminous Elo model, an important point has to be made.
The main component of the MSE is the π∗(i) − π(i) term, and therefore a low MSE depends on
7
For detailed discussions on the pros and cons of the MSE, consult Wang and Bovik (2009) and Girod (1993).
8
The details of how this optimiser works can be found division 7.6 of Appendix.
8
14. how close the expected probability π(i) is to the observed probability π∗(i). As π∗(i) is simply 1
(probability that winner player has won the match), the key here are the values of the π(i)s. These
π(i)s are computed using the players’ ratings, so if the ratings are inaccurate, the π(i)s will be
inaccurate and hence the MSE will be high. Recall that in line 4 of Algorithm 1, all initial ratings
are set to the arbitrary and hence clearly incorrect value of 1000. Therefore the players that are
new in the dataset will most likely have a bad effect on the MSE of the model. However this does
not mean that the model is deficient, it simply means that the players need to play a number of
matches before they attain their suitable rating and so should be included in the calculation of the
MSE. This could be thought of as a certain burn-in period.
Let β denote the number of matches a player has had to play in order to reach an Elo rating
considered ”appropriate”. This burn-in period feature can be incorporated into our basic algorithm
by replacing line 9 of Algorithm 1 by the lines:
In other words, we only consider those for matches for the calculation of the MSE, where both
players have played more than β matches. Also note, that when finalising the MSE in line 13 of
Algorithm 1, we no longer divide mse by the total number of matches N, but by the number of
matches N∗ that satisfied the condition (nWplay(i) > β & nLplay(i) > β).
But the question still remains: what would be an appropriate value for β? There is no perfect
answer to this question, as a combination of two things has to be considered. Intuitively, the greater
β gets, the more accurate the Elo ratings will be in the matches that are taken into account, and
hence the lower the MSE. However as β increases, there will be fewer and fewer matches in the
dataset where both players have played more than β matches. Let us take a quick look at the table
below to get an idea.
β 0 10 20 30 40 50 100
MSE×10−2 21.36 21.05 20.99 20.94 20.85 20.78 20.59
Data % 100% 85% 76% 68% 63% 57% 37%
Table 2: Table helping to determine a good value for the burn-in period β
This table nicely illustrates the decrease of the MSE, as well as the decrease of the size of the
remaining data for computation of this MSE, as we increase β. The most important thing to point
out, is the size of the MSE reduction between β = 0 and β = 10. This demonstrates the point we
were making earlier in this section: players not having played enough matches to have a suitable
rating, falsify the value of the error measure by quite a bit. So choosing any value for β above 10
would not be a mistake.
However in order to compare different Elo models, it is vital to keep the value of β fixed across
all models. Hence for the remainder of Section 3, we choose to work with a burn-in of β = 30.
This seems to be a good burn-in period, as a meaningful two-third of the data is still kept for the
calculation of the MSE. Also, 30 represents roughly the number of matches an average tennis
player plays in half a season, hence a new player would attain a suitable Elo rating in about 6
months.
9
15. 3.1.5 First Results
It is now finally time for our first proper results. After having found k = 240.6 by optimisation, we
attain MSE = 20.947×10−2 for the fixed values α = 1/2000 and β = 30. Running Algorithm 1 for
these parameter values and the date 2015-08-01 allows us to present the following Elo rankings9:
Elo Ranking Player Name Elo Rating
1 Djokovic N. 9934.3
2 Federer R. 8201.6
3 Murray A. 7663.6
4 Nadal R. 6855.2
5 Nishikori K. 6387.6
6 Berdych T. 6177.4
7 Del Potro J.M. 6052.4
8 Ferrer D. 5957.2
9 Wawrinka S. 5950.8
10 Raonic M. 5504.9
11 Gasquet R. 5256.3
12 Tsonga J.W. 5134.3
13 Monfils G. 4910.3
14 Cilic M. 4805.7
15 Simon G. 4791.7
16 Dimitrov G. 4761.0
17 Anderson K. 4561.1
18 Isner J. 4148.8
19 Fish M. 3913.0
20 Troicki V. 3727.2
Table 3: Ranking table given by the optimised Algorithm 1
These rankings should not look too unfamiliar to my fellow tennis fans! Note that Elo ratings
are real number, here however they have been rounded to one decimal place.
Recall from Section 3.1.1, that plugging two Elo ratings into the Elo function gives us the
probability estimate of Player 1 winning the match. So for example if we are interested in finding
the probability πD of Djokovic beating Federer, we simply calculate:
πD = ξ(RDjo, RFed) =
1
1 + e−(9934.3−8201.6)/2000
= 0.704 (4)
So based on the given ratings, Djokovic has a 70.4% chance of beating Federer on the specified
date. Given another date, Djokovic and Federer’s level of tennis would be different than what it is
for the currently specified date, and as an Elo rating represents a measure of a player’s level at one
point in time, both Djokovic and Federer’s ratings would be something different. Consequently the
value of πD would also change. In Figure 2, we can take look at the evolution of the Elo ratings of
Federer, Nadal, Djokovic and Murray (commonly referred to as the Big Four).
It would also be interesting to know how the evolution of these ratings compares to the evolution
of the Big Four’s ATP ranking points over the same period. This is shown in Figure 3.
9
Inactive players and players with less than 30 matches have been excluded from all ranking tables.
10
16. Observing Figures 2 and 3, we are glad to be able to spot a vague resemblance. However, we
also point out a major difference: the ratings given by the Elo model seem to evolve more closer
together, whereas the ATP ranking points undergo some serious fluctuations! Computations like
Equation (4) illustrate that Elo ratings actually have a mathematical interpretation; whereas on
the other hand, things are not as clear for the ATP points, as they originate from a much more
arbitrary principle. Further comparison between the two systems will be conducted in Section 3.3.2.
As a final note in this section, we ought to mention a potential weakness of the Elo model. The
Elo theory runs under the assumption of associativity 10. In other words, if Player 1 is better than
Player 2 and Player 2 is better than Player 3, then Player 1 is better than Player 3. However, there
are occasional ”cyclic” relationships that associativity, and hence the Elo, cannot identify. Using
a tennis example, it would be fair to say that Nadal’s game is effective against Federer, Federer’s
game causes Djokovic trouble, but Djokovic’s game works well against Nadal. But models that
would detect such cyclic interactions are far more complex and probably would not be great for
ranking tasks...
10
In fact, almost all ranking systems require this cornerstone assumption, and in the vast majority of the cases this
causes no problem.
11
17. Figure 2: Timeline showing the evolution of the Big Four’s Elo ratings (given by Algorithm 1) over the
years
Figure 3: Timeline showing the evolution of the Big Four’s ATP ranking points over the years. (Note: The
vertical dotted line represents the date on which the ATP point system has been slightly amended. In this plot,
all ATP points prior to this date are multiplied by a factor of two in order to compensate for the previous
system...)
12
18. 3.2 Extending the Elo
The main selling point of the Elo rating system is that it gives a very good approximation of reality:
a victory is evidence of an elevation of strength; a defeat is indication of a lowering of strength.
In the previous section, we described how this idea can be incorporated in a basic tennis setting.
However there is more to tennis however than just winning and losing! Tennis is a sport with
multiple features and some of these can be nicely built into an Elo model.
The set-up of a tennis match has two main components: the match format and the surface it is
played on. Both these have a significant impact on the final outcome of the match and so they will
be treated in the upcoming two sections.
3.2.1 Set Specific Elo
In tennis there are two types of match formats: best of 3 and best of 5 set matches. The best of 3
set match is the standard format, used in most tournaments (81% of the total matches of tennis1),
as they take less time. Best of 5 set matches (19% of matches), are only played by men in the
Grand Slam matches and in the Davis Cup...
Recall that two Elo ratings can be combined using the Elo function to obtain a probability.
But this probability can be chosen to represent anything that suits our needs! Throughout Section
3.1, it was chosen to be the probability that Player 1 wins the match. In this section however, we
decide that plugging two ratings into the Elo function will result in giving the probability of Player
1 winning a set. In order to understand why this choice is made, let us look at Algorithm 2, that
makes the distinction between the 3 and 5 set match formats. The notation used is the same as the
one employed in Algorithm 1.
Let us explain this algorithm. The first remark that can be made, is that its structure is very
similar to Algorithm 1. The only major difference is the addition of lines 9 to 18, where this
algorithm treats best of 3 and best of 5 set matches separately. A best of 3 set match can either be
won with a set score of 2:0 or with the set score 2:1. We note that this model makes the simplifying
assumption that the set-win probability π (i) stays constant throughout the entire match. Hence for
a given a π (i), the probability π
(i)
20 of winning the match 2:0 is simply given by (π (i))2 (line 10). In
order to win a match in 3 sets, one can either lose the first set or lose the second set. By observing
that (1 − π (i)) is the probability of Player 1 losing a set, the probability π
(i)
21 of him winning the
match with a set score of 2:1 is given by (1 − π (i))(π (i))2 + π (i)(1 − π (i))π (i) (line 11). As these
are the only two possible ways of winning a best of 3 set match, adding up these two probabilities
gives us the match-win probability (line 12).
Computing the match-win probability for a best of 5 sets match is of similar essence, just with
a bit more combinatorics involved. Let us denote by W a set won by the winner, and by L a set
won by the loser of the match. For the two match formats, the following combination possibilities
arise:
Best of 3:
(2:0) WW −→ 1 combination
(2:1) WLW, LWW −→ 2
13
19. Algorithm 2 SET ELO
1: Fix parameter k
2: Fix burn-in β
3: Set mse := 0
4: Initialise ratings Rm := 1000 for m in 1 → M
5: for i in 1 → N do
6: Compute the probability π (i) := ξ(R
(i)
W , R
(i)
L ) of the winner winning a set in match i, where
R
(i)
W and R
(i)
L are the ratings of the winner and loser of match i respectively
7: if nSets(i) = 3 then
8: π
(i)
20 := 1 × π (i) × π (i)
9: π
(i)
21 := 2 × π (i) × π (i) × (1 − π (i))
10: π(i) := π
(i)
20 + π
(i)
21
11: else if nSets(i) = 5 then
12: π
(i)
30 := 1 × π (i) × π (i) × π (i)
13: π
(i)
31 := 3 × π (i) × π (i) × π (i) × (1 − π (i))
14: π
(i)
32 := 6 × π (i) × π (i) × π (i) × (1 − π (i)) × (1 − π (i))
15: π(i) := π
(i)
30 + π
(i)
31 + π
(i)
32
16: end if
17: if nWplay(i) > β & nLplay(i) > β then
18: mse := mse + (π∗(i) − π(i))2
19: end if
20: R
(i)
W := R
(i)
W + k × (π∗(i) − π(i))
21: R
(i)
L := R
(i)
L − k × (π∗(i) − π(i))
22: end for
23: Let N∗ be the number of matches in tennis1 satisfying nWplay > β & nLplay > β.
24: Finalise MSE := mse/N∗
14
20. Best of 5:
(3:0) WWW −→ 1
(3:1) WWLW, WLWW, LWWW −→ 3
(3:2) WWLLW, WLLWW, LLWWW, LWLWW, LWWLW, WLWLW −→ 6
The number of different combinations for each case justifies the multiplicative factor in front of
the probability of a particular case happening.
By including this distinction between these two types of match formats, the match-win probabil-
ity π(i) should in general be more accurate than it was before this upgrade. Hence we would expect
a lower MSE than the one obtained in Section 3.1.5. After finding k = 151.2 by optimisation, we
reach a slightly lower error measure of MSE = 20.914 × 10−2 for the fixed values α = 1/2000 and
β = 30. Running Algorithm 2 for these parameter values and the date 2015-07-26, we obtain the
following Elo ranking table:
Elo Ranking Player Name Elo Rating
1 Djokovic N. 6442
2 Federer R. 5418
3 Murray A. 5100
4 Nadal R. 4583
5 Nishikori K. 4343
6 Berdych T. 4188
7 Del Potro J.M. 4143
8 Ferrer D. 4081
9 Wawrinka S. 4052
10 Raonic M. 3785
11 Gasquet R. 3640
12 Tsonga J.W. 3545
13 Monfils G. 3431
14 Simon G. 3376
15 Cilic M. 3356
16 Dimitrov G. 3333
17 Anderson K. 3215
18 Isner J. 2948
19 Fish M. 2807
20 Bautista R. 2691
Table 4: Elo ranking table given by the optimised Algorithm 2
The first reassuring remark that can be made, is that the players are ranked in nearly the exact
same order as the rankings in Table 3. However, extremely similar rankings were to be expected, as
both algorithms used the exact same matches and date. The major differences are the Elo ratings
themselves. We notice that the magnitudes of these ratings are smaller and more tightly clustered
than the previous ones. The reason for this, is that sets are shorter and hence for a given match-up,
sets have a more volatile outcome than matches. This causes, that for a given pair of players, the
set-win probability of the favourite is always less than his match-win probability. Hence in order
for the Elo ratings to reflect this, they need to be smaller and denser together.
15
21. Let us now compute the probability πD of Djokovic winning a set against Federer. This can be
done using the familiar Elo function:
πD = ξ(6442, 5418) = 0.625 (5)
So based on these ratings, Djokovic has a 62.5 % chance of winning a set against Federer. Assuming
that this set-win probability stays constant throughout the match, using calculations presented in
lines 10-12 of Algorithm 2, we work out that Djokovic’s match-win probability in a best of 3 set
match against Federer to be 0.684. To find this probability between these two players for a best of
5 set match, we apply lines 14-17 from Algorithm 2 and get 0.725. This illustrates nicely that the
longer the match format, the higher the likelihood that the favourite will eventually prevail.
We also observe, that adding this extra piece of information about the match format gives us
match-win probabilities on both sides of πD = 0.704 found in Section 3.1.5. This could was to be
expected, as by not taking into account the match format, we anticipate πD to be of a ”neutral”
nature. This is exactly the case for our Djokovic versus Federer example: 0.684 < 0.704 < 0.725.
The format of the match is not the only valuable pre-match information available: we also
know what surface the match is played on. Let us now move on to discussing how this additional
specification can be included in our Elo model.
3.2.2 Surface Specific Elo
One of the key things characterising a tennis match, is the type of surface it is played on. Tennis
is played on three different types of surfaces:
1. Clay - the slowest surface, having 34% of matches of tennis1 played on it
2. Hard - the middle-speed surface, encompassing 55% of the matches
3. Grass - the fastest surface, accounting for 11% of the matches
The game styles of a player may suit certain surfaces but not others. For example, Federer’s
game is particularly effective on grass, whereas Nadal’s style is exceptionally powerful on clay.
Our Elo rankings from the previous sections do not take into account surface types. Therefore
in this section, we are going to extend our previous algorithms so that the valuable information
contained in knowing the surface of a match is exploited.
In what follows, we make the realistic assumption that tennis players do not play the same level
of tennis on every surface. Hence each player will have 3 distinct Elo ratings: a hard, a clay and a
grass court rating. Making use of the same notation seen in Algorithms 1 and 2, let us take a look
at Algorithm 3, which generates these surface specific Elo ratings for every player.
We now comment on the new features that can be found within this algorithm. Unlike Algorithm
1 and 2, this one makes a distinction for the three different surface types. Not having one general
rating, but three different ratings, one for each surface, does this. These surface specific ratings are
initialised in line 7.
Using the if-statement in line 10, the algorithm separates cases depending on the surface. Con-
sequently the estimated set- and hence match-win probabilities are computed using surface specific
ratings corresponding to the surface of the match at hand.
16
22. Algorithm 3 SURFACE ELO
1: Fix hard court parameters hh, hc, hg
2: Fix clay court parameters cc, ch, cg
3: Fix grass court parameters gg, gh, gc
4: Fix burn-in β
5: Set mse := 0
6: Initialise surface specific ratings Rh,m := 1000, Rc,m := 1000 and Rg,m := 1000 for m in 1 → M
7: for i in 1 → N do
8: if Surface(i) = j for j ∈ (h, c, g) then
9: Compute π (i) := ξ(R
(i)
j,W , R
(i)
j,L), where R
(i)
j,W and R
(i)
j,L are respectively the winner and
the loser ratings on surface j of match i
10: if nSets(i) = 3 then
11: π
(i)
20 := π (i) × π (i)
12: π
(i)
21 := 2 × π (i) × π (i) × (1 − π (i))
13: π(i) := π
(i)
20 + π
(i)
21
14: end if
15: if nSets(i) = 5 then
16: π
(i)
30 := π (i) × π (i) × π (i)
17: π
(i)
31 := 3 × π (i) × π (i) × π (i) × (1 − π (i))
18: π
(i)
32 := 6 × π (i) × π (i) × π (i) × (1 − π (i)) × (1 − π (i))
19: π(i) := π
(i)
30 + π
(i)
31 + π
(i)
32
20: end if
21: if nWplay(i) > β & nLplay(i) > β then
22: mse := mse + (π∗(i) − π(i))2
23: end if
24: R
(i)
h,W := R
(i)
h,W + jh × (π∗(i) − π(i))
25: R
(i)
h,L := R
(i)
h,L − jh × (π∗(i) − π(i))
26: R
(i)
c,W := R
(i)
c,W + jc × (π∗(i) − π(i))
27: R
(i)
c,L := R
(i)
c,L − jc × (π∗(i) − π(i))
28: R
(i)
g,W := R
(i)
g,W + jg × (π∗(i) − π(i))
29: R
(i)
g,L := R
(i)
g,L − jg × (π∗(i) − π(i))
30: end if
31: end for
32: Finalise MSE := mse/N∗
17
23. The main upgrade in this algorithm comes in the rating update step displayed in lines 27-32.
We notice that after each match, the update is not only done for the relevant surface ratings, but
also for the other two sets of ratings.
The justification for this is based on common sense. For example, a victory on grass is not
solely an indication of an elevation of level as a player on grass, but also a sign for the increase of
level in general. Hence not only the grass court rating should increased, but also the clay and hard
court ratings. The inverse argument can be applied for defeats. We therefore require different 9
parameters to govern the magnitude of these updates:
• hh = 198.2 , parameter scaling the effect of a hard court match on the hard court ratings
• hc = 144.5 , effect of hard court match on clay court ratings
• hg = 164.4 , effect of hard court match on grass court ratings
• cc = 261.8 , effect of clay court match on clay court ratings
• ch = 180.2 , effect of clay court match on hard court ratings
• cg = 138.2 , effect of clay court match on grass court ratings
• gg = 261.8 , effect of grass court match on grass court ratings
• gh = 188.2 , effect of grass court match on hard court ratings
• gc = 138.2 , effect of grass court match on clay court ratings
Attached to each parameter are their optimised values. The relative magnitudes of these pa-
rameters are interesting to comment on. We notice, that a match has the biggest impact on the
surface rating that match was played on, as hh > hc, hg, cc > ch, cg and gg > gh, gc. Hard court
is considered to be the average speed surface: faster than clay, but slower than grass. Looking at
the hard court parameters, we see that a hard court match has a roughly equal effect on the clay
and grass court ratings (slightly more on grass court ratings, hinting that the speed of hard courts
are slightly tilted toward the speed of grass courts...). Now observing the clay court parameters,
we see that the result of a clay court match has some effect on hard court ratings, however it has
relatively small impact on the much faster grass surface. Similar phenomenon can be observed for
grass: a grass court match has sizable impact on the mid-speed hard court ratings, however it does
not effect the slower clay court ratings too much. These last two remarks make intuitive sense:
results on a slow court only slightly effect fast court ratings, and match outcomes on a fast court
only marginally impacts slow court ratings.
Let us now look at the results we get from this surface specific algorithm. Using the optimised
parameter values from above, we attain the much improved error measure of MSE = 20.568×10−2
for α = 1/2000 and β = 30. Running Algorithm 3 for these parameter values and the date
2015-07-26, we obtain the surface specific Elo rankings presented in Table 5.
18
24. Rank Clay Ratings Hard Ratings Grass Ratings
1 Djokovic N. 6877 Djokovic N. 6894 Djokovic N. 6746
2 Nadal R. 5822 Federer R. 5919 Federer R. 6180
3 Murray A. 5157 Murray A. 5578 Murray A. 5803
4 Federer R. 5150 Nishikori K. 4710 Berdych T. 4450
5 Wawrinka S. 4917 Berdych T. 4462 Nishikori K. 4360
6 Ferrer D. 4875 Wawrinka S. 4252 Del Potro J.M. 4139
7 Nishikori K. 4637 Del Potro J.M. 4240 Gasquet R. 4024
8 Del Potro J.M. 4397 Raonic M. 4142 Cilic M. 3989
9 Berdych T. 4298 Nadal R. 3845 Tsonga J.W. 3834
10 Gasquet R. 4037 Ferrer D. 3844 Wawrinka S. 3727
11 Raonic M. 3816 Tsonga J.W. 3761 Nadal R. 3686
12 Tsonga J.W. 3804 Cilic M. 3760 Raonic M. 3677
13 Monfils G. 3727 Simon G. 3731 Simon G. 3640
14 Dimitrov G. 3720 Gasquet R. 3729 Dimitrov G. 3629
15 Simon G. 3404 Monfils G. 3628 Ferrer D. 3557
16 Anderson K. 3285 Isner J. 3563 Anderson K. 3482
17 Thiem D. 3283 Anderson K. 3431 Monfils G. 3435
18 Cilic M. 3132 Dimitrov G. 3373 Karlovic I. 3381
19 Almagro N. 3128 Sock J. 2924 Fish M. 3171
20 Cuevas P. 3092 Fish M. 2871 Isner J. 3160
21 Sock J. 3058 Troicki V. 2829 Haas T. 3085
22 Bautista R. 3008 Bautista R. 2746 Seppi A. 3079
23 Fognini F. 2958 Haas T. 2744 Troicki V. 3036
24 Kohlschreiber P. 2919 Tomic B. 2681 Sock J. 2963
25 Robredo T. 2915 Goffin D. 2669 Lopez F. 2930
26 Andujar P. 2890 Dolgopolov A. 2647 Bautista R. 2859
27 Monaco J. 2881 Muller G. 2619 Tomic B. 2809
28 Mayer L. 2858 Querrey S. 2602 Mahut N. 2798
29 Bellucci T. 2793 Robredo T. 2592 Kohlschreiber P. 2796
30 Garcia-Lopez G. 2783 Thiem D. 2577 Kyrgios N. 2716
31 Isner J. 2768 Karlovic I. 2569 Querrey S. 2716
32 Verdasco F. 2722 Seppi A. 2475 Mayer F. 2669
33 Seppi A. 2698 Kohlschreiber P. 2413 Istomin D. 2633
34 Troicki V. 2695 Pospisil V. 2409 Verdasco F. 2618
35 Haas T. 2691 Kyrgios N. 2393 Dolgopolov A. 2607
36 Goffin D. 2636 Baghdatis M. 2353 Goffin D. 2603
37 Dolgopolov A. 2582 Verdasco F. 2345 Muller G. 2589
38 Paire B. 2544 Almagro N. 2310 Bolelli S. 2561
39 Bolelli S. 2543 Benneteau J. 2253 Baghdatis M. 2427
40 Klizan M. 2531 Bolelli S. 2247 Mannarino A. 2409
41 Chardy J. 2422 Lopez F. 2230 Pospisil V. 2406
42 Sousa J. 2418 Johnson S. 2209 Stepanek R. 2397
43 Kyrgios N. 2398 Istomin D. 2207 Tursunov D. 2381
44 Berlocq C. 2376 Janowicz J. 2179 Llodra M. 2378
45 Coric B. 2339 Coric B. 2176 Lu Y.H. 2307
46 Karlovic I. 2303 Monaco J. 2164 Janowicz J. 2301
47 Delbonis F. 2272 Sousa J. 2156 Thiem D. 2268
Table 5: Surface specific Elo ranking tables given by the optimised Algorithm 3
19
25. These are remarkable results, as it illustrates that the algorithm picks up beautifully on the
surface preferences of players. For example, it points out players like Nadal (clay=2, hard=9,
grass=11), Ferrer (6, 10, 15) or Fognini (23, 73, 68) who perform better on slower surfaces; and it
also identifies players like Federer(4, 2, 2), Cilic (18, 12, 8) or Isner (31, 15, 20) who love the faster
surfaces.
These ratings also allow us to compute match-win probabilities for any match-up, any desired
match format and any surface of our choice! Applying the familiar computations along the lines 8-20
from Algorithm 3, we can find match-win probabilities for Djokovic beating Federer for different
match set-ups. We summarise this in the following table:
πD Clay Hard Grass
Best of 3 79% 68% 60%
Best of 5 84% 72% 63%
Table 6: Djokovic’s match-win probability against Federer for different match set-ups, obtained by using our
surface specific Elo raings.
This illustrates nicely how Federer’s game style should cause Djokovic more and more trouble
the faster the court they play on.
Note that Algorithm 3 has six different values of π to choose from, whereas Algorithm 2 only
has two and Algorithm 1 only has a single one. This is the reason why Algorithm 3 outperforms its
ancestors.
To round off this section, let us look at some intriguing timeline plots on the next pages,
illustrating the evolution of the surface specific ratings of the Big Four.
20
26. Figure 4: Timeline showing the evolution of the Big Four’s clay court Elo ratings. Notice the reign of the
king of clay Rafa Nadal, only recently losing his throne to Djokovic
Figure 5: Timeline showing the evolution of the Big Four’s hard court Elo ratings. Spot the Federer’s
dominance in the early years, but a much more disputed fight from 2009 onwards.
21
27. Figure 6: Timeline showing the evolution of the Big Four’s grass court Elo ratings. Similar to the hard
court ratings, underlining the fact that grass and hard court game styles go hand-in-hand.
Figure 7: Timeline showing the evolution Federer’s surface specific Elo ratings. It is interesting to remark
the strong correlation between the three ratings. The Elo model picks up beautifully on Federer playing the
best clay court tennis of his life when winning the French Open in 2009.
22
28. 3.3 The Future of the Elo
So now that we obtain nice results and can get hold of good match-win probabilities, is it time to
run off to the bookies and try to make some money betting on tennis matches? Not quite. There
are still couple of key issues that have to be kept in mind. We start off this section by discussing
these.
3.3.1 Further Improvement Opportunities
So the question remains: how good is actually our Elo model? The short answer would be: it is
very good, but far from perfect. So what is still missing?
The main thing missing from our current Elo model is the handling of player injury. Those that
follow tennis might have noticed that players like Del Potro, Fish or Haas are ranked much higher
then they ought to be. Del Potro has been injured for nearly a year now, has undergone multiple
wrist operations and probably has a hard time holding a racket in his hand at this very moment!
However our Elo still ranks him 7 in the world, which is obviously wrong. The reason Elo misranks
injured players is simple. Remember that a player’s Elo rating only changes after that player has
played a match. However if a player is injured, he will not be playing any matches, hence his rating
will stay unchanged until he gets over the injury and starts being active again.
There could be multiple ways of dealing with this problem caused by this injury time-out.
Probably the most intuitive solution would be to apply an appropriate decay function δ to injured
players’ ratings. If we suppose that the number of days d since a player has last played a match is a
good indication of the player’s injury status, then when a player plays his first match after an injury
time-out of d days, his rating would no longer be the rating R0 that he had when he got injured,
but rather δ(d) × R0. Obviously, for small d (i.e. the player is not injured), we would expect δ to
satisfy something like δ(d) × R0 ≈ R0. The next thing we would have to find is an appropriate
decay function that improves the model performance. As long as the error measure is reduced, δ
could take any form: linear, piecewise linear, quadratic, exponential, etc. It should also be noted,
that retirement could be considered as a particular case of injury (think of it as ”injury for life”)
and hence also be dealt with using this decay function approach...
A second and also quite promising improvement we could make to our Elo model is taking the
completion status of matches into account. Was a match completed (96% of matches in tennis1) or
did a player win because his opponent abandoned (4% of matches)? In our current Elo model, if
a weaker player beats a higher rated player because that one abandons, the increase in the weaker
player’s rating will be that same as if he would have been victorious in a fully contested match.
This obviously is not right and hence has to be dealt with.
The most straightforward way of handling this is by introducing an additional parameter φ that
further scales the magnitude of the rating update. So if a match ends by abandon, the size of the
update in lines 10-11 of Algorithm 1 would be φ × k × (π∗(i) − π(i)). We would expect φ < 1, as
we have φ = 1 for completed matches. Including this additional feature into our algorithm should
allow us to hope for a decreased error measure.
There is further room for improvement by taking care of some of the simplifying assumptions
that have been made. Remember, in Section 3.2.1, we have assumed constant set-win probability
23
29. throughout the entire match. This obviously is not true, and let us show why by giving a simple
demonstration. Let us assume we have a 0.5 prior probability for Player 1 winning a set against
Player 2. Say if Player 1 wins the first set, common sense dictates that his probability of winning
the second set is now more than 0.5 and so we ought to update our prior to something more suitable
like 0.6 for example. Hence the match-win probability with score 2:0 would not be 0.5 × 0.5 but
0.5 × 0.6 instead.
Generalising this idea, the first step would be to define a strictly increasing function w, such
that w : [0, 1] → [0, 1], w(0) = 0, w(1) = 1 and w(π ) > π for π ∈ (0, 1). This function would
have the role of increasing the set-win probability of the winner of the current set by an appropriate
amount. For our previous little example, we would have had w(0.5) = 0.6. Then if we define a
function l to be one that decreases the set-win probability if the current set is lost, then a wise
choice for l would be the inverse of w. In other words, after having won and lost equal amount of
sets, the set-win probability will once again just be the prior: l(w(π)) = π. So in the case of best
of 3 sets, the match win probability would be calculated by summing the probability of winning
2:0 plus the probability of winning 2:1 having lost the first set plus the probability of winning 2:1
having lost the second set:
π = π × w(π ) + (1 − π ) × l(π ) × w(l(π )) + π × (1 − w(π )) × l(w(π )) (6)
Similar computations could be applied to best of 5 set matches. If we manage to find an appropriate
w function, this methodology will allow us to get better match-win probabilities and hence we can
hope for improved error measures.
3.3.2 Elo vs. ATP Rankings
The official ATP rankings have been in place since 1973. It allows the ranking of professional tennis
players using a very comprehensible method, presented in detail in division 7.2 of the Appendix.
It is highly important for these rankings to be accurate, because apart from being an indication of
relative strength, it is used to determine which players are allowed to enter which tournaments, as
well as the seedings11 for all tournaments. But how good are these ATP rankings actually? How
good are they in comparison to our Elo rankings?
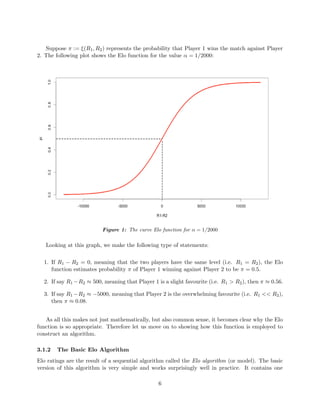
Let us first look at these rankings from the point-of-view of match prediction. How often does
the higher ranked player win? To give us an idea on how good of a predictor a ranking system is,
a worthy indicator could be the percentage of times the higher ranked player wins. If the higher
ranked player wins 100% of the time, that ranking system would be considered to be perfect; whereas
a ranking system forecasting the higher ranked to win only 50% of the time should be considered
as a baseline, as its prediction power is no better than a coin-flip.
For the current ATP rankings, the higher ranked player wins 65.6% of time. This is a solid value,
far better than the baseline 50%, and hence its usage in the real world is nowhere near catastrophic.
However this value is 66.7% for our Elo rankings from Section 3.2.1 and as high as 67.6% for our
surface specific Elo in Section 3.2.2. These represent respectively a 7% (66.7−65.6
65.6−50 × 100%) and a
13% improvements compared to the ATP rankings. Hence one might rightfully argue that the Elo
ranking systems developed in this thesis is a strong competitor of the current one.
11
For a full explanation on what tennis seedings are, go to the en.wikipedia.org/wiki/Seed(sports) website.
24
30. But the official ATP rankings have further weaknesses. In 2008 Rafael Nadal was in devastating
form, winning nearly every tournament he entered. That year in won the French Open and Wim-
bledon back-to-back, however on the eve of lifting the most prestigious trophies in tennis, he was
still ranked as the second best player in the world behind Roger Federer. It was only three months
later, when Nadal went on to win the Olympic Games, that he ascended to the number 1 ranking.
Most experts and fans, had long since come to the conclusion that Nadal was the best player in
the world, the implication being that the official ATP rankings were rather slow in reflecting what
everyone else already knew. So the big question is: how does our Elo ranking system behave in this
situation? In order to visualise the difference between the ATP and the Elo rankings, let us plot
the evolution of Nadal’s rankings across the years for both ranking systems.
Figure 8: Visual comparison of Nadal’s ATP and Elo ranking along the years
This graph reveals beautiful results in favour of the Elo. Looking at this figure, we can spot with
ease that the Elo ranking system seems to always be a step ahead of the ATP rankings. In 2008, the
Elo already ranked Nadal as world number 1 even before Wimbledon started and not three month
after he has won it! In 2012, Nadal had a very mediocre year. In the first half of the season he
kept on losing to his main rivals and he skipped the second half of the season for injury reasons.
However the Spaniard came roaring back in 2013, winning (nearly) every possible trophy on the
calendar year of the ATP World Tour. The Elo model immediately picked up on Rafa’s bombastic
form and quickly put him back to the top of rankings. On the other hand, the official ATP rankings
where once again slow to react. Due to his injury from the previous year, Nadal lacked ATP points,
and by the time he collected all points he needed to be the official world number 1, his good form
25
31. started fading away...
Nadal’s example is just one amongst the many where the Elo outperforms the official rankings.
The ranking evolution of Latvian tennis player Ernest Gulbis is another flagrant example of this.
Gulbis is one of the most talented players in the world of tennis, however he is mainly known for
the inconsistency of his form and his volatile mood. Gulbis reached the semi-finals of the French
Open last year beating Federer on the way, played the best tennis of his life and reached a career
high of world number 10 on official ATP rankings. However, the decline that came afterwards was
one of the most astonishing ones in tennis history. Not having any injury problems, Gulbis played
week-in week-out on Tour and in a period of 8 months (November 2014 - June 2015) managed to
win only a single match! Let us look at the timeline of Gulbis’ rankings to get a comparative idea:
Figure 9: Visual comparison of Gulbis’ ATP and Elo ranking along the years
This figure clearly illustrates Gulbis’ drought during that eight-month period. However once
again this plot makes it obvious that the Elo reacts much quicker to what is actually happening
than the official ATP rankings do. A second thing that we can note from this figure is that the
Elo rankings are slightly less extreme than the ATP rankings, which once again might be a point
in favour of the Elo. And having in mind that our Elo model is far from its highest potential,
one might seriously start questioning the authority of the current rankings. In my opinion, the old
fashioned ATP rankings ought to be replaced by a more Elo-like ranking system.
26
32. 4 Point-by-Point Probability Analysis
The second goal of this thesis is to find a method that allows us to track the evolution of a tennis
player’s match-win probability whilst a match is in-play. A match that is in-play, is one that has
already started, and as point are played one after the other, the score is constantly evolving. Points
are the building blocks of a tennis match: points make up games, games make up sets and sets
make up the match. Hence the outcome of each point played is a source of information that allows
us to update our belief about the end result of the match. As this update can be made on a
point-by-point basis, knowing the probability of each player winning the next point is key in order
to find the evolution of match-win probabilities of an in-play tennis match. We explain how these
point-win probabilities can be obtained in Section 4.1. Then in Section 4.2, we present a model
that gives us match-win probabilities for any given match score. Finally, in Section 4.3, we use an
example of a famous tennis match to present the operations of our model, and we also explain how
the importance of each point of the match can be measured.
But before we dive in, we have to highlight an assumption that we make throughout this entire
section. Henceforth we will assume, that points in tennis are independent and identically distributed
(i.i.d.), and so the on-serve point-win probabilities of players stay constant for the entire duration of
a match. This is a common assumption made in the literature (Schutz (1970), Carter Jr and Crews
(1974) or Barnett and Clarke (2005)), as it hugely simplifies computations. In reality however,
tennis points are not i.i.d. This is proven in works by Klaassen and Magnus (2001) or Jackson and
Mosurski (1997), however for our purposes, it is a decent assumption to work with. As a potential
extension to this thesis, we might want look into replacing this simplification by something more
advanced...
4.1 On-Serve Point-Win Probabilities
For a point in tennis, a player can either be the one serving or the one returning the serve. Serving
is a huge advantage: on average, the server wins his service point 64.0% of the time. This percentage
varies from one surface to another. On a fast surface like grass, the serve bounces faster and lower
off the court, therefore it is harder to return, resulting in an increased average point-win percentage
of 66.8%. However, all the opposite is true on the slower clay, hence servers win only 62.4% of their
serves on average. This statistic is 64.4% for hard courts. These percentages give us a nice feel
about the significance of the surface type in a tennis match.
Levels of serve vary from player to player, and so do levels of returns. Some players are better at
serving, other better at returning. The best players are good at both. Consequently, the on-serve
(and return) point-win probabilities vary for every particular match-up. For example, the on-serve
point win probability of a player will be lower against a good returner than against a weaker one.
Assuming that every tennis player has a quantifiable service and return level, we find ourselves once
again in an Elo-like set-up!
At this point, some might wonder: Why not just simply reverse engineer the match-win proba-
bilities obtained in Section 3 to retrieve point-win probabilities? The reason we cannot do this, is
because we are interested in making the distinction between service and return point-win probabili-
ties. If our interest would lie in knowing general point-win probabilities (which is not of great value
in tennis to be honest), a reverse engineering method could work. Let us give a simple example
for further clarification. Suppose we have two matches: in Match 1, both players have an on-serve
point-win probability of 0.9, and in Match 2, both players’ on-serve point-win probability is 0.6. It
27
33. is easy to see, that in both matches, Player 1 has a match-win probability π1 of 0.5. However, if the
only information that we are given is π1 = 0.5, then it is impossible to know whether this comes
from Match 1 or Match 2. Hence we will need to use yet another variation of the Elo algorithm to
find the probabilities of our interest.
The fundamentals used for this Elo task are similar to those discussed in Section 3. But instead
of creating a rating system for each of the three surfaces, we will produce six sets of ratings: a
service and a return set of ratings for each of the three surfaces. Recall from Section 2.2, that the
dataset tennis2 contains the fraction of on-serve points won by the winner (pW), as well as this
fraction (pL) for the loser of every match. As we have assumed points to be i.i.d., we will consider
these fractions to be the observed value for the on-serve point-win probabilities that are estimated
by the Elo model in each loop. Making use of the same notation employed in the algorithms from
Section 3 and our permanently fixed value of α = 1/2000, Algorithm 4 allows us to achieve the
desired results.
Let us comment on this algorithm. The first observation we can make, is that its fundamental
structure is very similar to that of Algorithm 3. The main extension is that this algorithm’s
dimensionality is twice as big, as a distinction between service and return is made. Hence there are
twice as many parameters than what we had previously. The notation we used for the parameters
is also very similar: for example hcR is the parameter that controls the magnitude of the effect a
hard court match has on the clay return Elo ratings.
Secondly, we might wonder why all service ratings are initialised at 2000 and all return ratings
at 1000. As mentioned above, the server wins the point 64% of the time on average, so it would be
clever to choose initial ratings that reflect this. In this algorithm, the on-serve point-win probability
ρ is obtained by using the Elo function to combine the service rating of the server with the return
rating of the returner. Thus a smart choice for RjS,m and RjS,m for j ∈ (h, c, g) would be one that
satisfies:
0.64 ≈ ξ(RjS,m, RjR,m) =
1
1 + exp(−(RjS,m − RjR,m)/2000)
(7)
Choosing the friendly integers RjS,m = 2000 and RjR,m = 1000 we get the value of 0.622, which is
good enough. Having these as initial ratings will also give us a nice spread for the ratings in the
end result, hence we shall stick with them.
Also, notice that by subtracting respectively the observed and estimated on-serve point-win
probabilities from 1, we can obtain the observed and estimated return point-win probabilities. The
simple reason for this is that a tennis point is either won by the server or the returner; there is no
other possibility.
The error measure update step of this algorithm presented in lines 15-17, is similar to the one
found in Algorithm 3: the closer the estimated probability is to the observed one, the smaller the
error. The only dissimilarity is that here two squared error terms are added to the mse, as there
are two estimated probabilities (ρ
(i)
W and ρ
(i)
L ) for each match.
Finally, the six ratings for both the winner and the loser player are updated one-by-one in
lines 18-25 in similar fashion as in Algorithm 3. However there is one small thing to bring to our
attention. For the update of the return ratings (i.e. when K = R in line 18), the magnitude of the
update should naturally depend on the difference between the observed return point-win fraction
γ∗ and estimated return point-win probability γ. However as these are just given by γ∗ ≡ 1 − ρ∗
and γ ≡ 1 − ρ. Hence their difference can simply be written as:
γ∗
− γ ≡ (1 − ρ∗
) − (1 − ρ) ≡ ρ − ρ∗
≡ −(ρ∗
− ρ) (8)
28
34. Algorithm 4 SERVICE ELO
1: Fix service hard court parameters hhS, hcS, hgS
2: Fix return hard court parameters hhR, hcR, hgR
3: Fix service clay court parameters ccS, chS, cgS
4: Fix return clay court parameters ccR, chR, cgR
5: Fix service grass court parameters ggS, ghS, gcS
6: Fix return grass court parameters ggR, ghR, gcR
7: Fix burn-in β
8: Set mse := 0
9: Initialise service surface specific ratings RhS,m := 2000, RcS,m := 2000 and RgS,m := 2000 and
return surface specific ratings RhR,m := 1000, RcR,m := 1000 and RgR,m := 1000 for m in
1 → M
10: for i in 1 → N do
11: if Surface(i) = j for j ∈ (h, c, g) then
12: Compute ρ
(i)
W := ξ(R
(i)
jS,W , R
(i)
jR,L), the on-serve point-win probability of the winner of
match i, where R
(i)
jS,W is the service rating of the winner and R
(i)
jR,L is the return rating of the
loser of match i on surface j
13: Also compute ρ
(i)
L := ξ(R
(i)
jS,L, R
(i)
jR,W )
14: Let ρ
∗(i)
W denote the observed fraction of service points won by the winner of match i and
let ρ
∗(i)
L denote this fraction for the loser.
15: if nWplay(i) > β & nLplay(i) > β then
16: mse := mse + (ρ
∗(i)
W − ρ
(i)
W )2 + (ρ
∗(i)
L − ρ
(i)
L )2
17: end if
18: for K ∈ (S, R) do
19: R
(i)
hK,W := R
(i)
hK,W + jhK × (ρ
∗(i)
W − ρ
(i)
W )
20: R
(i)
hK,L := R
(i)
hK,L − jhK × (ρ
∗(i)
L − ρ
(i)
L )
21: R
(i)
cK,W := R
(i)
cK,W + jcK × (ρ
∗(i)
W − ρ
(i)
W )
22: R
(i)
cK,L := R
(i)
cK,L − jcK × (ρ
∗(i)
L − ρ
(i)
L )
23: R
(i)
gK,W := R
(i)
gK,W + jgK × (ρ
∗(i)
W − ρ
(i)
W )
24: R
(i)
gK,L := R
(i)
gK,L − jgK × (ρ
∗(i)
L − ρ
(i)
L )
25: end for
26: end if
27: end for
28: Finalise MSE := mse/N∗
29
35. The additional minus sign at the front will just be absorbed by the multiplicative parameter and
hence the algorithm will work just fine.
So let us get on to looking at the results given by this algorithm. We first optimise the parameters
of this algorithm for α = 1/2000 and β = 10 and attain an error measure of MSE = 6.244 × 10−3.
This value is clearly not comparable to those obtained in Section 3, the reason for this being that
here we are estimating on-serve point-win probabilities and not match-win ones. By their nature,
estimates of on-serve point-win probabilities will be closer to their observed values then estimates
of match-win probabilities to their observed values, hence a much lower MSE was to be expected.
Running Algorithm 4 for the optimised parameter and the date 2015-08-01, we can produce the
Elo rankings presented in Tables 8, 9 and 10.
Once again we get very nice results. The model perfectly identifies big servers like Karlovic
(211cm tall), Isner (208cm) or Raonic (196cm) and ranks them high up the service rankings. Excel-
lent returners like Ferrer (175cm), Nishikori (179cm) or Simon (182cm) can be spotted towards top
of the return rankings. And the best players in the world like Djokovic (188cm), Federer (186cm)
or Murray (191cm) can be found high up both types of rankings!
As a quick side-note, looking at the heights of these players, we can spot an interesting trend.
Obviously in order to be good server, being tall is a massive advantage, as permits the serve to be
hit from higher up. On the other side of the spectrum, good returners are generally the shorter
players, as that allows them to be more dynamic and move around the court with more agility. But
to be outstanding in tennis, both good serving and returning skills are required. So the conclusion
of this mini data analysis is that the ideal height for a male tennis player is in the range 185-190cm.
To wrap up this section, let us look at some point-win probabilities that can be obtained from
the above ratings. Ivo Karlovic might be the best server in the world, but he is also the worst
returner with his clay, hard and grass court return ratings being 332, 349 and 366 respectively.
So for Federer serving, let us compare his on-serve point-win probabilities when, on the one hand
serving to Ferrer, on the other to Karlovic. Using the Elo function like in Equation (7), we obtain
the following comparative table summarising Federer’s chances of winning a point on-serve:
ρF Clay Hard Grass
Ferrer 64% 68% 72%
Karlovic 79% 80% 80%
Table 7: Federer’s on-serve point-win probability on the different surfaces when serving to Ferrer or Karlovic
Hence we conclude that Federer will have an easier time winning service points against Karlovic
than against Ferrer. This table also nicely highlights that the quicker the surface, the easier to win
service points.
30
36. Rank Clay Service Ratings Clay Return Ratings
1 Karlovic I. 3187 Nadal R. 1918
2 Raonic M. 3044 Ferrer D. 1896
3 Federer R. 3036 Djokovic N. 1872
4 Isner J. 3015 Murray A. 1665
5 Djokovic N. 2994 Nishikori K. 1642
6 Anderson K. 2699 Simon G. 1553
7 Berdych T. 2666 Garcia-Lopez G. 1495
8 Wawrinka S. 2658 Monfils G. 1490
9 Murray A. 2637 Federer R. 1487
10 Tsonga J.W. 2626 Andujar P. 1459
Table 8: Service and return clay court Elo ranking table given by the optimised Algorithm 4
Rank Hard Service Ratings Hard Return Ratings
1 Karlovic I. 3319 Djokovic N. 1958
2 Federer R. 3152 Murray A. 1761
3 Raonic M. 3122 Ferrer D. 1689
4 Isner J. 3107 Federer R. 1609
5 Djokovic N. 3053 Nadal R. 1524
6 Anderson K. 2776 Nishikori K. 1522
7 Berdych T. 2744 Simon G. 1502
8 Wawrinka S. 2722 Berdych T. 1403
9 Murray A. 2688 Seppi A. 1323
10 Tsonga J.W. 2682 Bautista R. 1320
Table 9: Service and return hard court Elo ranking table given by the optimised Algorithm 4
Rank Grass Service Ratings Grass Return Ratings
1 Karlovic I. 3439 Djokovic N. 1700
2 Federer R. 3267 Murray A. 1573
3 Isner J. 3183 Federer R. 1518
4 Raonic M. 3157 Ferrer D. 1329
5 Djokovic N. 3064 Berdych T. 1299
6 Berdych T. 2837 Simon G. 1287
7 Anderson K. 2802 Nishikori K. 1283
8 Wawrinka S. 2737 Seppi A. 1280
9 Muller G. 2722 Gasquet R. 1239
10 Tsonga J.W. 2711 Bautista R. 1233
Table 10: Service and return grass court Elo ranking table given by the optimised Algorithm 4
31
37. 4.2 Match-Win Building Blocks
In Section 3, we saw how the Elo methodology can be used to estimate match outcome probabilities.
However, as a tennis match gets under way and more and more points are played, the initial
(or prior) match-win probability changes. What does this match-win probability look like for an
intermediate score in the match? In this section, we develop a model that can determine the match-
win probability of a player for any inputted score of a match. Works by Huang et al. (2011) and
Barnett et al. (2006) served as great inspiration for this section.
4.2.1 Finding Game-Win Probabilities using Markov Chains
The scoring system of a tennis match is a bit like the Russian Matryoshka dolls: within a match are
sets, within sets are games and within games are points. Firstly, we shall concentrate on how points
make up a game; more specifically, how can the game-win probability be found once the point-win
probability is known. To begin with, let us present the structure of a tennis game:
Figure 10: Structure of a game in tennis.
It should be noted that the notation for the scoring of a game is unnecessarily complicated: one
point is denoted by 15, two points by 30 and three points by 40. In order to win a game, one has
to win four points with at least two points difference. So say at three points a piece (i.e. deuce or
40:40), Player 1 would need a point score of 5:3 (or G:40) to win the game, etc. 12
At this point, an interesting remark can be made. Mathematically speaking, the score 30:30 is
no different from 40:40; in both cases one of the players will require at least two points in a row to
win the game. Similar remark is true for 40:30 and A:40; Player 1 requires one point to win the
12
See division 7.1 of the Appendix for a full explanation of the tennis scoring system.
32
38. game, whereas if Player 2 wins the next point, the score will go back to deuce. By symmetry, the
same is true for 30:40 and 40:A. Hence the Figure 10 can be simplified to:
Figure 11: Simplified structure of a game in tennis, used for the Markov chain computations.
Contemplating this figure, two words seem to be screaming out: Markov chains! This graph
looks just like a transition diagram of a discrete-time Markov chain: the arrows symbolise the
transition probabilities and the scores represent the states of the Markov chain. And in fact, this
problem can indeed be looked at from a Markov chain perspective so let us quickly familiarise
ourselves with some basic Markov chain theory.
Definition 1. A Markov chain is a sequence {Xk} of random variables that have the Markov
property; meaning that, given the present state, the future and past states are independent. Formally,
Pr(Xk+1 = x|X1 = x1, X2 = x2, . . . , Xk = xk) = Pr(Xk+1 = x | Xk = xk) (9)
if both conditional probabilities are well defined, i.e. if Pr(X1 = x1, ..., Xk = xk) > 0.
Let Ψ represent the state space of the Markov chain. The single-step transition probabilities of
the Markov chain are given by:
ρij := Pr(Xk+1 = j | Xk = i) (10)
for k ∈ N and i, j ∈ Ψ. The set of all these transition probabilities gives a probabilistic summary
of transition dynamic of the Markov chain. This information is most commonly represented by a
33
39. transition matrix P, a |Ψ| × |Ψ| matrix with ρij as its (i, j)th entry. For a more detailed account on
Markov chain theory, Kemeny and Snell (1960) or Isaacson and Madsen (1976) provide excellent
further reading opportunities.
So let us apply the above theory to our tennis game example. But before we do so, we underline
an important assumption that we make. For the remainder of Section 4, we will work with the
simplifying assumption that the point-win probability (on-serve and return) of a tennis player stays
constant throughout the entire match. This is not completely true in reality, but it is a decent
approximation to make, as simplifies computations quite a bit. This is similar to the constant
set-win assumption made in Section 3.2.1, and this also would merit further investigation in future
studies...
Looking at Figure 11, we can say that the point score within a game can be treated as a discrete-
time Markov chain with 21 states and transition probabilities ρ (dark green arrows) and q := 1 − ρ
(bright green arrows). Here is what the transition matrix corresponding to Figure 11 looks like:
P =
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 0 ρ q 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 0 0 ρ q 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 ρ q 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 ρ q 0 0 0 0 0 0 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0 ρ q 0 0 0 0 0 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0 0 ρ q 0 0 0 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0 0 0 ρ q 0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0 0 0 0 ρ q 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0 0 0 0 0 ρ q 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0 0 0 0 ρ q 0 0 0 0 0 0
11 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ρ q 0 0 0 0
13 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ρ q 0 0 0
14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ρ q 0 0
15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
17 0 0 0 0 0 0 0 0 0 0 0 0 q 0 0 0 0 0 0 ρ 0
18 0 0 0 0 0 0 0 0 0 0 0 0 ρ 0 0 0 0 0 0 0 q
19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
20 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
21 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Let us make a few remarks about this transition matrix. It points out clearly that once the
Markov chain gets to state 11, 15, 16, 19, 20 or 21, it will stay there forever. These states are
called absorbing states and correspond to a scores where the game is over. All other states are
transient, as once the Markov chain leaves these states, there is a chance that it will never come
back: Pr(Xk+n = i | Xk = i) < 1 for k ∈ N and n ∈ N∗.
Theorem 1. Let P be the transition matrix of a Markov chain, and let u(0) be the probability vector
representing the starting distribution. Then the probability that the chain is in state i after n steps,
is given by the ith entry in the vector
u(n)
= u(0)
Pn
. (11)
34
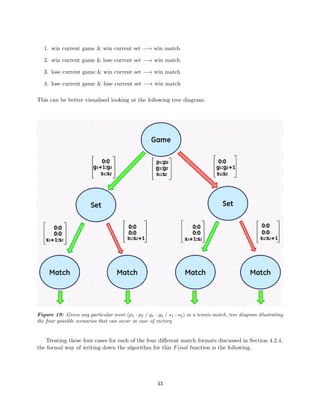
40. Basically what this theorem 13 is telling us, is that if we know the initial distribution and the
transition matrix of a Markov chain, the entire dynamics of the chain can be deduced. Let us
demonstrate this using an example. Suppose that two players are at the beginning of a game at 0:0
(State1) and we are given that ρ = 0.5. Hence our initial vector is defined to be the following:
> state <- 1
> u0 <- matrix(0,1,21)
> u0[state] <- 1
> u0
[,1][,2][,3][,4][,5][,6][,7][,8][,9][,10][,11][,12][,13][,14][,15][,16][,17][,18][,19][,20][,21]
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Then the first point of the game is played. The chain can either move to State2 with probability
ρ = 0.5 or to State3 with probability 1 − ρ = 0.5. This is illustrated by applying Equation (11) the
above theorem:
> u0 %*% (P %^% 1)
[,1][,2][,3][,4][,5][,6][,7][,8][,9][,10][,11][,12][,13][,14][,15][,16][,17][,18][,19][,20][,21]
0 0.5 0.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Continuing this process for 2, 3, 4, 5 and 6 points played, the probability distribution evolves
the following way:
> u0 %*% (P %^% 2)
[,1][,2][,3][,4][,5] [,6][,7][,8][,9][,10][,11][,12][,13][,14][,15][,16][,17][,18][,19][,20][,21]
0 0 0 0.25 0.5 0.25 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
> u0 %*% (P %^% 3)
[,1][,2][,3][,4][,5][,6] [,7] [,8] [,9] [,10][,11][,12][,13][,14][,15][,16][,17][,18][,19][,20][,21]
0 0 0 0 0 0 0.125 0.375 0.375 0.125 0 0 0 0 0 0 0 0 0 0 0
> u0 %*% (P %^% 4)
[,1][,2][,3][,4][,5][,6][,7][,8][,9][,10] [,11][,12] [,13][,14] [,15][,16][,17][,18][,19][,20][,21]
0 0 0 0 0 0 0 0 0 0 0.063 0.25 0.375 0.25 0.063 0 0 0 0 0 0
> u0 %*% (P %^% 5)
[,1][,2][,3][,4][,5][,6][,7][,8][,9][,10][,11][,12][,13][,14][,15] [,16] [,17] [,18] [,19][,20][,21]
0 0 0 0 0 0 0 0 0 0 0.063 0 0 0 0.063 0.125 0.313 0.313 0.125 0 0
> u0 %*% (P %^% 6)
[,1][,2][,3][,4][,5][,6][,7][,8][,9][,10][,11][,12][,13][,14][,15] [,16][,17][,18][,19] [,20] [,21]
0 0 0 0 0 0 0 0 0 0 0.063 0 0.313 0 0.063 0.125 0 0 0.125 0.156 0.156
We notice, that once an amount of probability arrives to an absorbing state, it stays there for-
ever. Remember, our main interest lies in finding the probability gρ that Player 1 wins the game.
This game-win probability is given by the sum of the probabilities of winning the game losing no
points; losing only one point; losing two points, plus the probability that the game goes to 40:40,
but it is still won.
13
The proof of this theorem can be found in Chapter 2.3 of Karlin (2014).
35
41. This summation can formally be written the following way:
gρ = Pr(G : 0) + Pr(G : 15) + Pr(G : 30) + Pr(40 : 40 ∩ G)
= Pr(G : 0) + Pr(G : 15) + Pr(G : 30) + Pr(40 : 40) × Pr(G|40 : 40)
= Pr(State11) + Pr(State16) + Pr(State20) + Pr(State13) × Pr(G|State13) (12)
From the above matrix computations, the probabilities Pr(State11), Pr(State16), Pr(State20)
and Pr(State13) are known. Therefore the only thing that is still to be found is Pr(G|State13).
This leads us to the following problem.
Problem 1. Player 1 is playing a tennis game against Player 2 and the score within the game is
40:40. If the probability of Player 1 winning a point is ρ, what is the probability D(ρ) that Player
1 wins the game?
In order to answer this question, we point out that Player 1 can win the game by either winning
the next two points or by winning the game after one more deuce or by winning the game after
passing through another 2 deuces or by winning the game after coming back to deuce 3 times etc.
Here is a graphical representation of the situation:
Figure 12: Structure of a game in tennis when starting from deuce
36
42. We can find the expression for D(ρ) going through the following steps:
D(ρ) = Pr(Player 1 wins game with the next 2 points) + Pr(Player 1 wins game after another deuce)+
Pr(Player 1 wins game after 2 deuces) + Pr(Player 1 wins game after 3 deuces) + ...
= ρ2
+ 2ρ2
[ρ(1 − ρ)] + 4ρ2
[ρ(1 − ρ)]2
+ 8ρ2
[ρ(1 − ρ)]3
+ ...
= ρ2
(1 + 2[ρ(1 − ρ)] + [2ρ(1 − ρ)]2
+ [2ρ(1 − ρ)]3
+ ...)
= ρ2
∞
n=0
[2ρ(1 − ρ)]n
=
ρ2
1 − 2ρ(1 − ρ)
using the geometric summation formula
∞
n=0
Xn
=
1
1 − X
if |X| < 1
(13)
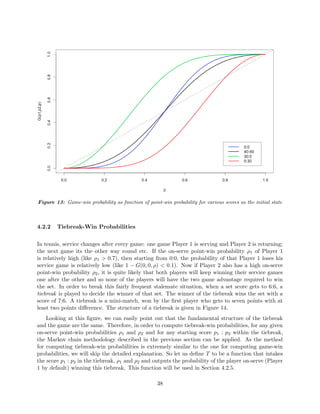
The black curve of Figure 13 plots D(ρ).
Returning to our initial example where we set ρ = 0.5, simple computations give us:
Pr(G|State13) = D(0.5) =
0.52
1 − 2 × 0.5 × (1 − 0.5)
=
0.25
1 − 2 × 0.25
=
0.25
0.5
= 0.5 (14)
And hence:
g0.5 = 0.0625 + 0.125 + 0.15625 + 0.3125 × 0.5 = 0.5 (15)
Concluding this example, if both players have an equal probability of winning a point, then starting
at 0:0, Player 1 has a 50% chance to win the game. This does not seem to be a surprising result
and one might even argue that it is pretty obvious to guess without all the Markov chain business!
However what if ρ = 0.5? What if ρ is something like ρ = 0.64? Applying similar computations as
above, we get the values needed for Formula (12):
g0.64 = Pr(State11) + Pr(State16) + Pr(State20) + Pr(State13) × Pr(G|State13)
= 0.168 + 0.242 + 0.217 + 0.245 × 0.760
= 0.813 (16)
Therefore if a player wins a point 64% of the time, this will result in him winning the game in about
81% of the cases. To picture this, we can look at the blue curve of Figure 13.
Thus far we only looked at game-win probabilities for the initial state being 0:0 and 40:40.
However the same method works perfectly for any other score being the initial state; the only thing
that needs to be changed is the initial distribution vector u(0). Let us define G to be a function that
intakes the point score (p1 : p2) within the game as well as the point-win probability ρ of the player
on-serve, and outputs the game-win probability of that player. As an end for this subsection, let us
take a look at how this function behaves for various point-scores as the initial state:
37
43. Figure 13: Game-win probability as function of point-win probability for various scores as the initial state
4.2.2 Tiebreak-Win Probabilities
In tennis, service changes after every game: one game Player 1 is serving and Player 2 is returning;
the next game its the other way round etc. If the on-serve point-win probability ρ1 of Player 1
is relatively high (like ρ1 > 0.7), then starting from 0:0, the probability of that Player 1 loses his
service game is relatively low (like 1 − G(0, 0, ρ) < 0.1). Now if Player 2 also has a high on-serve
point-win probability ρ2, it is quite likely that both players will keep winning their service games
one after the other and so none of the players will have the two game advantage required to win
the set. In order to break this fairly frequent stalemate situation, when a set score gets to 6:6, a
tiebreak is played to decide the winner of that set. The winner of the tiebreak wins the set with a
score of 7:6. A tiebreak is a mini-match, won by the first player who gets to seven points with at
least two points difference. The structure of a tiebreak is given in Figure 14.
Looking at this figure, we can easily point out that the fundamental structure of the tiebreak
and the game are the same. Therefore, in order to compute tiebreak-win probabilities, for any given
on-serve point-win probabilities ρ1 and ρ2 and for any starting score p1 : p2 within the tiebreak,
the Markov chain methodology described in the previous section can be applied. As the method
for computing tiebreak-win probabilities is extremely similar to the one for computing game-win
probabilities, we will skip the detailed explanation. So let us define T to be a function that intakes
the score p1 : p2 in the tiebreak, ρ1 and ρ2 and outputs the probability of the player on-serve (Player
1 by default) winning this tiebreak. This function will be used in Section 4.2.5.
38
44. Figure 14: Structure of the tiebreak
4.2.3 Set-Win Probabilities
We now arrive to the final building block of a tennis match: the set. There exist two types of set
formats: a format where a tiebreak is played at 6:6, and another format where no tiebreak is played
at 6:6 and the set continues normally until one of the players gains a two-game lead. Figures 15
and 16 illustrate these two set structures.
In both these cases, the underlying structure is once again the same as those encountered
previously, so fundamentally similar Markov chain computations can be applied to find the desired
set-win probabilities. Let us define S to be a function that intakes the score g1 : g2 of the set, ρ1, ρ2
and whether the set is allowed to have a tiebreak or not, and outputs the set-win probability of the
player on-serve. Let us look at a quick demonstration of the results this function gives. Suppose we
have ρ1 = 0.7 and ρ2 = 0.65. Then for the given scores, the chance of Player 1 winning the set for
the two set formats is summarised in this table:
S(score, ρ1, ρ2, TB?) 0 : 0 4 : 4 4 : 5 5 : 4
Tiebreak 66% 61% 54% 96%
No Tiebreak 67% 65% 59% 97%
Table 11: The chances of the set-win for different set scores as initial state, tiebreak or no tiebreak set and
for the given on-serve point-win probabilities ρ1 = 0.7 and ρ2 = 0.65
As ρ1 > ρ2, we can affirm that Player 1 is the favourite. The first thing we can point out when
looking at this table, is that the set-win percentages of the favourite are lower for the tiebreak
39
45. Figure 15: Structure of a set in tennis when a tiebreak is played at 6:6
Figure 16: Structure of a set in tennis, when no tiebreak is played at 6:6 and the set continues normally
till one of the players wins it with a two-game advantage
40
46. sets. This makes sense, as playing a tiebreak creates a quicker and more even ending to the set.
Consequently, we deduce that tiebreaks favour the underdog.
We can also notice that the set-win percentages are more even at 4:4 then at 0:0. The reason
for this is that at 4:4 the set is closer to its end and hence the set-win can swing easier to either of
the players, hence favouring the underdog.
We should also bear in mind, that the score is shown for the point of view of the server. So at
4:5, the Player 1 will serve to try to equalise to 5:5; however at 5:4, Player 1 is serving to win the set
6:4. And as the probability of him winning his service game is relatively high (G(0, 0, 0.7) = 0.9),
the percentages reflect nicely whether he is serving to equalise or serving to win the set.
4.2.4 Match-Win Probabilities
Our eventual interest is to find match-win probabilities. Recall from Section 3.2.1 that a tennis
match can either be best of 3 or 5 sets. Here are the structures for both:
Figure 17: Structure of a best of 3 set tennis match
Figure 18: Structure of a best of 5 set tennis match
41
47. Depending on the tournament, a tennis match can be one of the following four formats:
• Best of 3 sets with tiebreak in the final set (by far the most common format, played in most
tournaments)
• Best of 5 sets with no tiebreak in the final set (used in Grand Slam matches (excluding the
US Open) and the Davis Cup)
• Best of 5 sets with tiebreak in the final set (only used in the US Open)
• Best of 3 sets with no tiebreak in the final set (only used on the women’s circuit)
Given a particular set standing, match win probabilities for any match format can be obtained
using our beloved Markov chain methodology discussed in depth in Section 4.2.1, therefore we once
again will omit the details. So let us define M to be a function that intakes the set standing s1 : s2,
the on-serve point-win probabilities ρ1 and ρ2 and a match format chosen from the above four
possibilities, and outputs the match-win probability of the player on-serve. We will make good use
of this function in the section to come.
4.2.5 The Match-Win Probability Calculator
Armed with the functions G, T, S and M, we finally arrive to the point, where for any chosen score
in the match, the final match-outcome probabilities can be computed. We define Final to be a
function with the following intake:
1. p1 - The point score of Player 1 in the game or tiebreak
2. p2 - The point score of Player 2 in the game or tiebreak
3. g1 - The game score of Player 1 in the set
4. g2 - The game score of Player 2 in the set
5. s1 - The set score of Player 1 in the match
6. s2 - The set score of Player 2 in the match
7. ρ1 - The on-serve point-win probability of Player 1
8. ρ2 - The on-serve point-win probability of Player 2
9. bo - Match format? Best of 3 or 5 sets
10. tb - Final set tiebreak allowed? Yes (y) or No (n).
Final then outputs the match-win probability of the player on-serve at the next point (Player 1
by default). Notice that there is much more to this function then to our previous building-block
functions G, T, S and M. Remember that G and T outputted respectively a game- and tiebreak-win
probability given the specified point score; S gave the set-win probability given the inputted game
score; and M printed the match-win probability given a particular set standing. The function Final
combines these four building-block functions in a smart way in order to find the desired probability.
Given any score (p1 : p2 / g1 : g2 / s1 : s2) in the match, we identify four different possible ways to
eventually win the match:
42
48. 1. win current game & win current set −→ win match
2. win current game & lose current set −→ win match
3. lose current game & win current set −→ win match
4. lose current game & lose current set −→ win match
This can be better visualised looking at the following tree diagram:
Figure 19: Given any particular score (p1 : p2 / g1 : g2 / s1 : s2) in a tennis match, tree diagram illustrating
the four possible scenarios that can occur in case of victory
Treating these four cases for each of the four different match formats discussed in Section 4.2.4,
the formal way of writing down the algorithm for this Final function is the following.
43
49. Algorithm 5 The FINAL function
1: Fix p1, p2, g1, g2, s1, s2, ρ1, ρ2, bo and tb
2: Set σ := s1 + s2
3: if tb = y and bo = i for i ∈ (3, 5) then
4: if g1 = 6 or g2 = 6 then
5: π1 := G(p1, p2, ρ1) × (1 − S(g2, g1 + 1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, y)
6: π2 := G(p1, p2, ρ1) × S(g2, g1 + 1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, y)
7: π3 := (1 − G(p1, p2, ρ1)) × (1 − S(g2 + 1, g1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, y)
8: π4 := (1 − G(p1, p2, ρ1)) × S(g2 + 1, g1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, y)
9: else if g1 = 6 and g2 = 6 then
10: π1 := T(p1, p2, ρ1, ρ2) × (1 − S(g2, g1 + 1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, y)
11: π2 := T(p1, p2, ρ1, ρ2) × S(g2, g1 + 1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, y)
12: π3 := (1 − T(p1, p2, ρ1, ρ2)) × (1 − S(g2 + 1, g1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, y)
13: π4 := (1 − T(p1, p2, ρ1, ρ2)) × S(g2 + 1, g1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, y)
14: end if
15: end if
16: if tb = n and bo = i for i ∈ (3, 5) then
17: if g1 = 6 or g2 = 6 and σ < i − 1 then
18: π1 := G(p1, p2, ρ1) × (1 − S(g2, g1 + 1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, n)
19: π2 := G(p1, p2, ρ1) × S(g2, g1 + 1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, n)
20: π3 := (1 − G(p1, p2, ρ1)) × (1 − S(g2 + 1, g1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, n)
21: π4 := (1 − G(p1, p2, ρ1)) × S(g2 + 1, g1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, n)
22: else if g1 = 6 and g2 = 6 and σ < i − 1 then
23: π1 := T(p1, p2, ρ1, ρ2) × (1 − S(g2, g1 + 1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, y)
24: π2 := T(p1, p2, ρ1, ρ2) × S(g2, g1 + 1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, n)
25: π3 := (1 − T(p1, p2, ρ1, ρ2)) × (1 − S(g2 + 1, g1, ρ2, ρ1, y)) × M(s1 + 1, s2, ρ1, ρ2, i, n)
26: π4 := (1 − T(p1, p2, ρ1, ρ2)) × S(g2 + 1, g1, ρ2, ρ1, y) × M(s1, s2 + 1, ρ1, ρ2, i, n)
27: else if σ = i − 1 then
28: π1 := G(p1, p2, ρ1) × (1 − S(g2, g1 + 1, ρ2, ρ1, n)) × M(s1 + 1, s2, ρ1, ρ2, i, n)
29: π2 := G(p1, p2, ρ1) × S(g2, g1 + 1, ρ2, ρ1, n) × M(s1, s2 + 1, ρ1, ρ2, i, n)
30: π3 := (1 − G(p1, p2, ρ1)) × (1 − S(g2 + 1, g1, ρ2, ρ1, n)) × M(s1 + 1, s2, ρ1, ρ2, i, n)
31: π4 := (1 − G(p1, p2, ρ1)) × S(g2 + 1, g1, ρ2, ρ1, n) × M(s1, s2 + 1, ρ1, ρ2, i, n)
32: end if
33: end if
34: Output π1 + π2 + π3 + π4
44
50. At first glance, this function might be a bit scary, but in fact it is nothing but a bit fiddly. So
let us go through its tricky features in order to get a good grip on it.
The first thing we note, is that this function treats matches that can have a final set tiebreak
(lines 3-17) separately from those that cannot (lines 18-37). If there can be a final set tiebreak, that
means that a tiebreak could be played in every set and so we put tb = y as input for the functions
S and M. However, if only the final set cannot have a tiebreak, then this is reflected by putting
tb = n in all the M functions as well as tb = n in the S functions for the case of a final set (lines
29-33). If we define σ to be the number of sets already played (line 2), then if σ is equal to the
maximum number of sets allowed minus one (line 29), we know that the match is in its final set.
The second thing we pay attention to, is whether the inputted score is one from a game or a
tiebreak. If g1 = 6 or g2 = 6 (lines 4 and 19), the score is a game score and the function G is used.
However if g1 = 6 and g2 = 6 (lines 9 and 24), the given score is from a tiebreak and the function
T is employed.
Now let us clarify the most confusing aspect of this algorithm. We will use the example of line
7 for the clarification. In this line, we are interested in finding the probability π3 that Player 1 wins
the match, given that he loses the current game but wins the current set. As Player 1 is serving, the
probability of him winning the game from score (p1 : p2) is G(p1, p2, ρ1). Therefore the probability of
him losing this game is simply 1−G(p1, p2, ρ1). And as Player 1 loses the game, the set score becomes
(g2 + 1 : g1) from Player 2’s point of view. Player 2 is now on-serve however, and so the probability
of him winning the set is given by S(g2 + 1, g1, ρ2, ρ1, tb = y). Consequently the probability of
Player 2 losing and hence Player 1 winning the set is just 1 − S(g2 + 1, g1, ρ2, ρ1, tb = y). So now
the set count from the perspective of Player 1 is (s1 + 1 : s2), hence his match-win probability in a
best of i set match with possibility of tiebreak in the final set is M(s1 + 1, s2, ρ1, ρ2, bo = i, tb = y).
Multiplying all the relevant probabilities together, we can obtain our desired π3.
Having now a full understanding of how the function Final works, we can move on to our next
section that is filled with the juicy results!
45
