Download to read offline
Uploaded byBert Chenin
Experimental Xylophone. Study of transverse vibrations in a thin metal bar
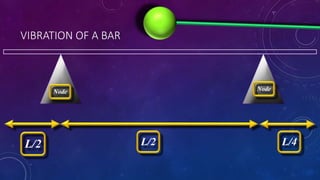
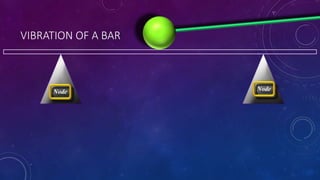
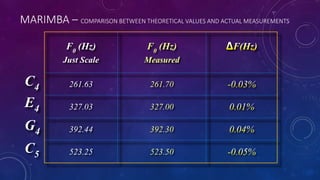
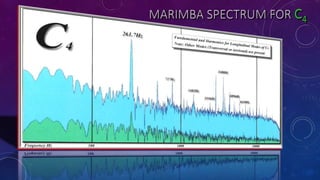
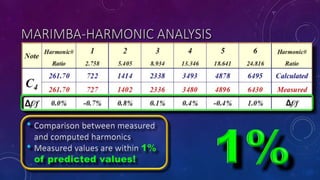
The document discusses the transverse vibration modes of a bar, emphasizing the fundamental frequency and deriving formulas related to the Young's modulus and density of aluminum. It highlights that the ratios for harmonics are not whole or rational numbers, indicating that a solid bar won't produce harmonious sounds. A comparison of theoretical and measured frequencies for musical notes on a marimba is also presented.
Experimental Xylophone. Study of transverse vibrations in a thin metal bar
- 5. VIBRATION OF ABAR L/2 L/4L/2 Node Node
- 6. VIBRATION OF ABAR Node Node
- 7. VIBRATION OF ABAR Node Node
- 8. VIBRATION OF ABAR Node Node
- 9. VIBRATION OF ABAR Node Node
- 10. VIBRATION OF ABAR Node Node
- 11. VIBRATION OF ABAR Node Node 𝑭 = 𝟑. 𝟎𝟏𝟏 𝟐 𝝅 𝟖 𝟏𝟐 𝒀 𝝆 𝑻 𝑳 𝟐 This transverse vibration mode is the fundamental The frequency F is Y is the young modulus = 69Gpa for Al ρ is the bulk density = 2700kg/m3 for Al T is the thickness = 0.00635m ¼” L is the length of the bar = 0.355 for C4
- 12. VIBRATION OF ABAR Node Node All the transverse modes are expressed as: 𝑭 = 𝝅 8 12 𝒀 𝝆 𝑻 𝑳2 3.0112, 52 , 72, … , 2𝒏 + 1 2, …
- 13. VIBRATION OF ABAR Node Node The ratios for the harmonics are: 0 1 2 3 4 5 6 Harmonic# 1 2.758 5.405 8.934 13.346 18.641 24.816 Ratio The ratios of harmonics are not whole or rational numbers. Therefore, a solid bar will not produce a “harmonious” sound.
- 16. MARIMBA – COMPARISONBETWEEN THEORETICAL VALUES AND ACTUAL MEASUREMENTS F0 (Hz) Just Scale F0 (Hz) Measured 261.63 261.70 327.03 327.00 392.44 392.30 523.25 523.50 C4 C5 E4 G4