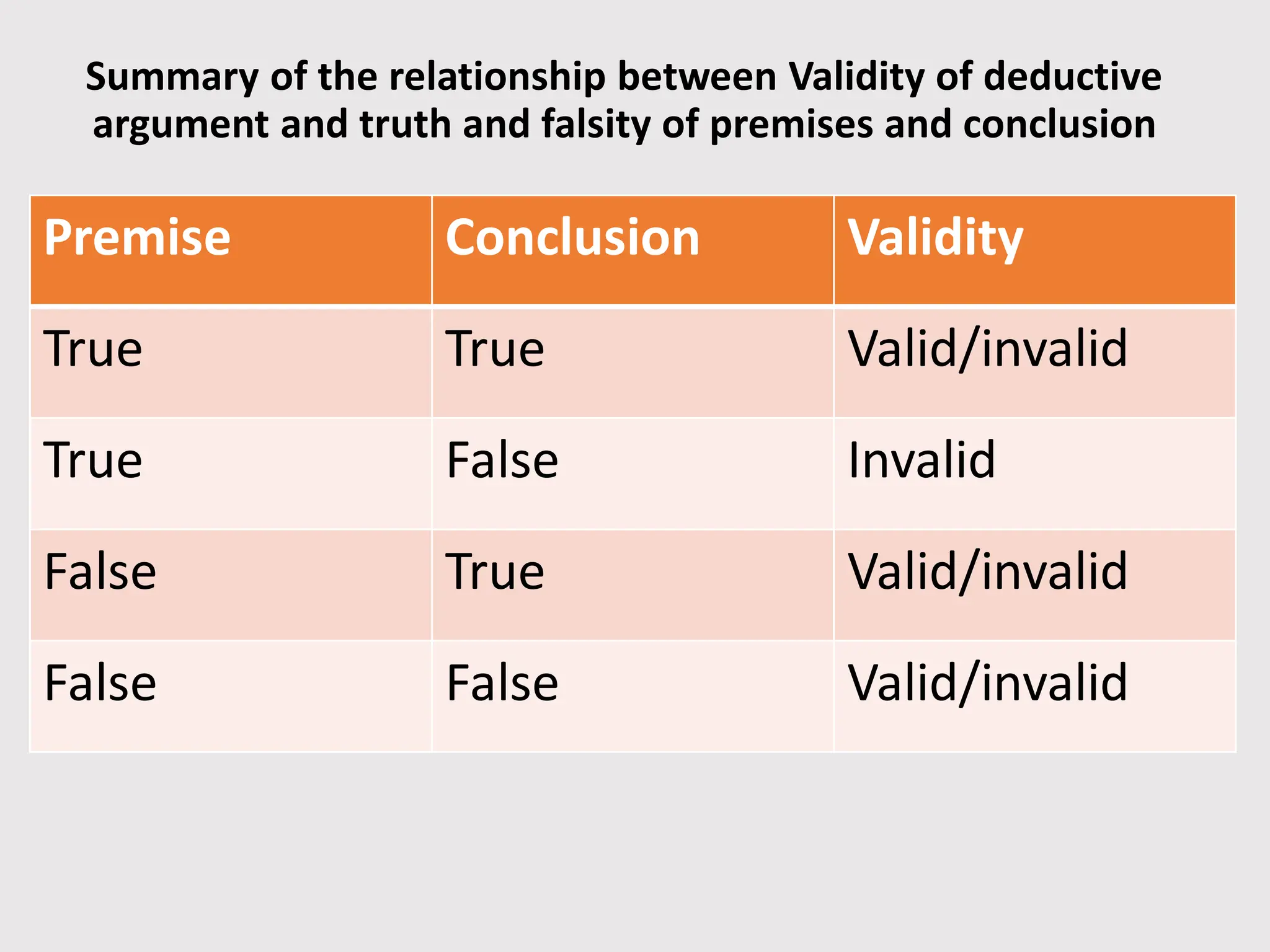
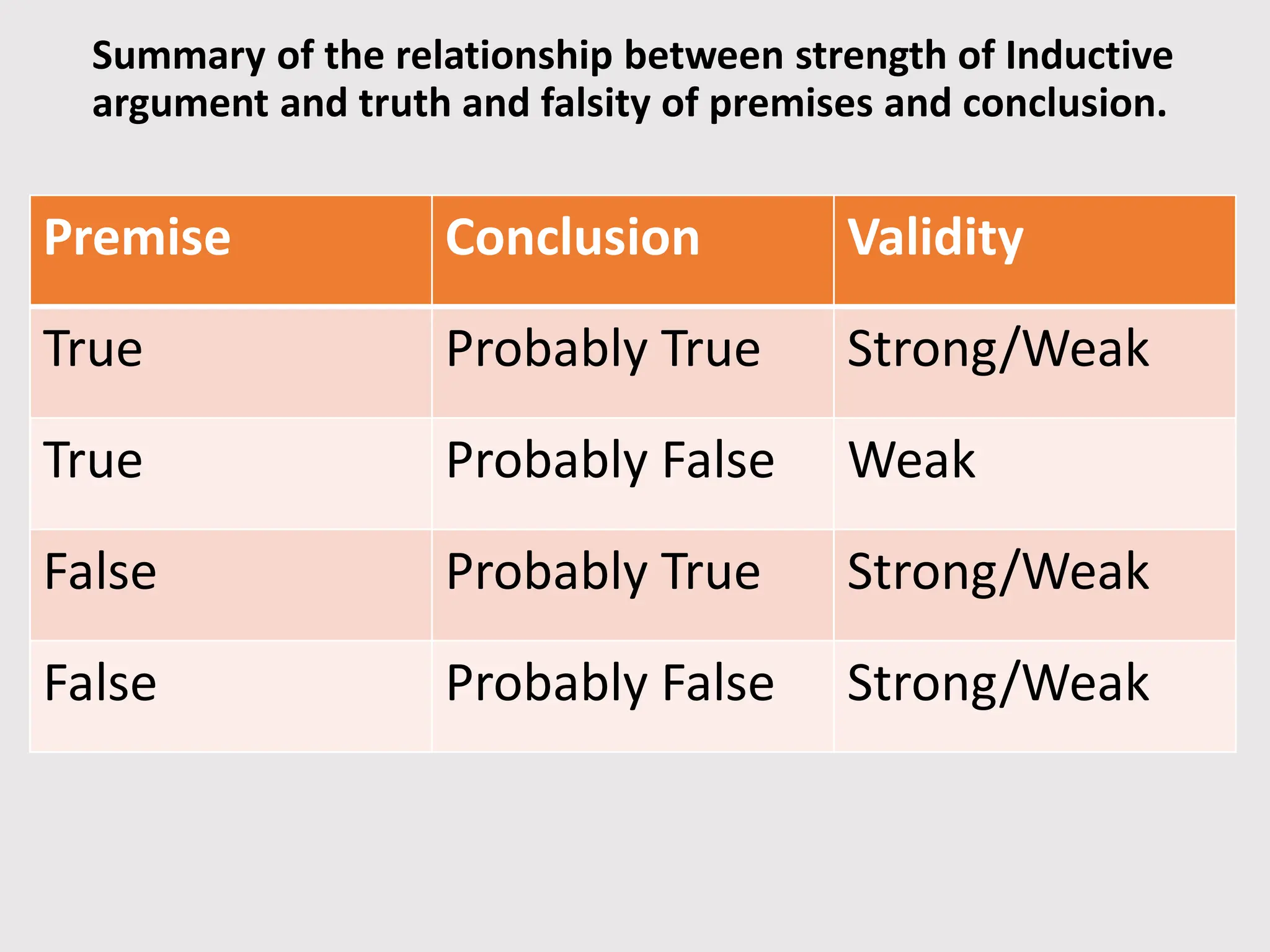
The document provides a comprehensive overview of logic for teachers, covering the nature of logic, the structure and types of arguments, and the distinctions between inductive and deductive reasoning. It details the concepts of truth, validity, and soundness within logical arguments, as well as common logical fallacies and their implications for teaching. Additionally, it emphasizes the importance of logic in education, aiding teachers in reasoning and decision-making.

1. Introduction to Logic
for Teachers

2. Topical outline
 Nature of logic; concept of logic,, structure of an argument,
inductive and deductive arguments, truth, validity and
soundness of arguments, importance of logic to the teacher.
 Fallacies; informal and formal Fallacies, application and
implication of Fallacies.
 Categorical statements; types and standards forms of
statements, Venn diagrams, distribution of terms, the square
of proposition.
 Syllogism; the characteristics of Syllogism, the mood and
figures, validity of Syllogism.
 Logic and languages methods of definition, truth tables.

3. Concept of logic
The word "logic" originates from the Greek word
"logos", which has a variety of translations, such
as reason, discourse, or language.
Traditionally defined as the study of the laws of
thought or correct reasoning.
Not restricted to one subject but to all subjects
As science it investigates, develops and systematizes
principles and methods that can be used to distinguish
between correct and incorrect reasoning .
As an art, because it helps the person to weigh
evidence, marshal and construct arguments

4. General importance of logic
Good ground for acting
Protects one being unduly influenced
Makes one more rational and more intellectually
aware
Its basis for both productive, collaboration and
effective and dependable leadership
etc

5. Group Assignment
Qn. Explain the importance
of logic to a primary
teacher?

6. Structure of Argument
An argument is a set of premises together with a
conclusion
Logic is interested in whether arguments are correct, i.e.
whether their premises support the conclusion
Premise(s) are the statements /propositions that
support or provide for the conclusion.

7. The premises can be one or many E.g.
1. All Africans are black
Therefore blacks live in Africa
2. Human beings are mammals
Khaukha is a human being
Khaukha is a mammal
NB. 1. Each statement in any of the arguments is
called a proposition
2. No proposition by itself is in isolation is either a
premise or conclusion.

8. Identifying Premise or Conclusion in
Argument
• This is done by recognizing and identifying special
terms that determine the different parts of a
particular argument
• Special terms/expressions are called premise
indicators and conclusion indicators
• Example of premise indicators are; since, because,
for, or as.
• Example of conclusion indicators are; therefore,
hence, thus or so.

9. Inductive and Deductive Arguments
Inductive Arguments
It follows the particular to general order or
sequence
Use specific premises or observations to make a
broader generalization.
e.g. Musa is good a teacher
Mariam is a good teacher
Therefore Moslems are good teachers
As teacher, you start by illustrating the idea which is
studied in order to generalize and make inferences

10. Deductive Arguments
• This type argument starts its reasoning from a
general principle to particular instances.
• E.g. The teacher states “Teachers are
knowledgeable”
• He/she gives examples to illustrate, such as because
“they teach all categories of the people” and “have
been trained for the job”

11. Truth and Validity of Arguments
• In ordinary language validity’ can be used
interchangeably with ‘truth’ and vice versa,
• But in Logic, validity applies only to arguments, and the
concept of truth applies exclusively to propositions.
• Thus, validity is an attribute of an argument
• Validity is about the logical connection between the
propositions
• An argument is valid if the relationship between its
components are so that the premises conclusively
prove the conclusion.

12. Cont…
• Conversely, if the conclusion is not a logical necessity,
then the argument is not valid, and it will be called an
invalid argument
• Validity as a “logical necessity” confines the concepts of
validity and invalidity to Deductive arguments only (this is
b’se deductive arguments make the claim that its premises conclusively support the conclusion, while
in case of Induction, the premises do not conclusively support the conclusion)
• The objective of deductive arguments is to establish that the
conclusion undeniably follows from the premises.
• When it achieves this objective, the argument is said to be valid,
and when it fails to achieve this objective then the argument is
invalid argument.

13. •How do we know that a deductive
argument has achieved its objective? How
do we ascertain whether the argument is
valid?
• The validity is determined by the relationship between the
premises and the conclusion.
• If the premises in an argument are true then the
conclusion can never be false. Therefore, this is a valid
argument.

14. Let us consider an example:
All Fast foods are unhealthy.
French Fry is a Fast Food.
Therefore, French Fry is Unhealthy.
The validity is determined by the relationship between the
premises and the conclusion.
If the object “French Fry” is included in the group of “Fast Food” (second premise)
and if “Fast food” is included in the group of “unhealthy” things (first premise),
then the object “French Fry” is necessarily included in the group of “unhealthy”
things(conclusion).
• You can see that the above relationship gives a
particular form of the argument and this form is a
valid one.

15. Cont…
• Interestingly if we use an argument with utterly false
propositions, yet fulfilling the same argument “form”
like the one given above, it will still be valid.
• All mammals have wings.
• All plants are mammals.
• Therefore, all plants have wings.
All the propositions in the above argument are false, but the argument is still
valid, because the logical relationship of the propositions is such that if the
premises were actually true, the conclusion would be certainly true.

16. Qn. Is there connection between the truth value of
the proposition and validity/ invalidity of the
argument?
Now you can recall;
The validity and invalidity of an argument depends on the
logical relationship between its propositions.
Propositions are constituent parts of an argument.
Every argument can have one proposition as conclusion
and at least two or more propositions as premises.
Each proposition can be true or false, and every
argument must be either valid or invalid.

17. Cont…
• There are several arrangements of truth/falsity and
validity/invalidity.
• These arrangements will provide crucial clues to
understand the relationship between truth and validity in
deductive Logic.
• Let us explore those arrangements with examples
Arrangement 1: True Premises, True Conclusion, Valid
Argument
Example: All mammals are animals.
All cats are mammals.
Therefore, all cats are animals.
In this argument, all the propositions are known to be true. The
premises conclusively establish the conclusion; therefore, making the
argument “valid”.

18. Arrangement 2: False Premises, False Conclusion, Valid
Argument
• Example:
All mammals are six legged animals.
All Ostriches are mammals.
Therefore, all Ostriches are six legged animals.
In this argument, all the propositions are known to be false. But here
the premises conclusively establish the conclusion, because if the
premises were actually true, the conclusion would have been
certainly true. Therefore, this argument is also valid.

19. Arrangement 3: True Premises, True Conclusion, Invalid
Argument
• Example:
If I won the UBC Show, I would be a millionaire.
I did not win the UBC show.
Therefore, I am not a millionaire.
The premises and conclusion here are true, the argument is invalid
because the conclusion does not necessarily follow from the
premises. This will be further clear from the next example.

20. Arrangement 4: True Premises, False Conclusion, Invalid
Argument
• Example:
If Sudhir Tata won the UBC Show, he would be a millionaire.
Sudhir doesn’t win the UBC show.
Therefore, Sudhir is not a millionaire.
In this argument the premises are true, but the conclusion is false in
reality. Mr. Sudhir till now didn’t participate in UBC show, but he is one
of the richest persons in Uganda. The argument is invalid because the
premises don’t conclusively establish the conclusion.

21. Arrangement 5: False Premises, True Conclusion, Valid
Argument
• Example:
All Fishes are mammals.
All dolphins are fishes.
Therefore, all dolphins are mammals.
The conclusion here is true in reality, but the premises are
unquestionably false. However, since there is a logically necessary
connection between the premises and the conclusion, because of
which the premises conclusively support the conclusion, the
argument is valid.

22. Arrangement 6: False Premises, True Conclusion, Invalid
Argument
• Example:
All mammals have wings.
All dolphins have wings.
Therefore, all dolphins are mammals.
This argument has two false premises and still the conclusion is true. However, the
argument is invalid, because the conclusion is not conclusively supported by the
premises. We know that by examining the form of the argument. Here, in the
second premise the group “all dolphins” belongs to the group “wings”, and in first
premise, the group “all mammals” belong to the group “wings”, and these don’t
prove whether the group “all dolphins” belong to the group “mammals”

23. Arrangement 7: False Premises, False Conclusion, Invalid
Argument
Example:
All mammals have wings.
All dolphins have wings.
Therefore, all mammals are dolphins.
In this argument both premises and conclusion are false. And the
argument is invalid. Because the conclusion is not supported by the
premises.

24. • Arrangement 8: True Premises, False Conclusion, Valid
Argument
• Example: Nil
By definition, in a deductively valid argument if the premises are
true, it is impossible for the conclusion to be false. If the conclusion is
false, when premises are true, that means the conclusion is not
conclusively supported by the premises. Therefore, the argument will
be always invalid. That is why there is no example of Arrangement 8

25. Summary of the relationship between Validity of deductive
argument and truth and falsity of premises and conclusion
Premise Conclusion Validity
True True Valid/invalid
True False Invalid
False True Valid/invalid
False False Valid/invalid

26. Does validity apply to inductive arguments?
• Validity as a “logical necessity” confines the concepts of
validity and invalidity to Deductive arguments only
• However, the terms “Strong” and “Weak” are used for
the evaluation of inductive arguments.
• Inductive argument is either weak or strong but not valid
or invalid.
• The objective of an inductive argument is to establish
that it is improbable for the conclusion to be false when
the premises are true.

27. Cont…
• The conclusion here has a probability of being
supported by the premises.
Example 1:
Every year in last decade there were always heavy rainfall
during month of May in Bugisu.
Therefore, probably there will be heavy rainfall in the in
the month of may of this year in Bugisu.
Example 1:
Every Ugandan president was an orator
Therefore, it is probable that the next will Ugandan
president also be an orator.
NB. In most cases inductive arguments are used to make
predictions about the future.

28. Cont…
• An inductive argument is strong when it achieves its
objectives.
• A weak inductive argument is the one which fails its
objective.
• In weak inductive argument, the conclusion does not
probably follow from the premises, even though it is
claimed so.
• The strength or weakness of the arguments depend on
its confirming instances

29. Summary of the relationship between strength of Inductive
argument and truth and falsity of premises and conclusion.
Premise Conclusion Validity
True Probably True Strong/Weak
True Probably False Weak
False Probably True Strong/Weak
False Probably False Strong/Weak

30. Soundness of Arguments
• A sound argument is a deductive argument that is valid
and it has true premises.
• It must satisfy two conditions: the argument must be
valid, and the premises must be true.
• If any of this condition is not met, then no valid
argument can be termed as sound.
• There is possibility of having an argument which is valid
but not sound.

31. Cont…
Consider the following argument:
All planets of the solar system revolve around the Sun.
The Earth is a planet of the Solar System.
Therefore, the Earth revolves around the Sun.
This argument is valid because the logical relation between the
propositions are so that if the premises were true, then the conclusion
would be certainly true. This argument is valid and in addition, the premises
here are actually true. So this is a Sound deductive arguments.

32. Cont…
• In contrast to Sound argument, unsound arguments are
those which do not satisfy the conditions of a sound
argument.
• To put it clearly:
1. An argument which is invalid is unsound.
2. An argument which is valid but has false premises is
unsound.
• Following these conditions, if we consider the eight
arrangements of truth and validity described in previous
slides, we shall find that only Arrangement No.1 is
sound.
• All other possible combinations of truth/falsity and
validity/invalidity are always unsound.
• All deductive arguments are either sound or unsound.

33. Individual Assignment
Qn. What are the
implications of the
inductive and deductive
arguments to you as a
classroom teacher?