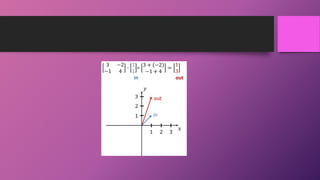
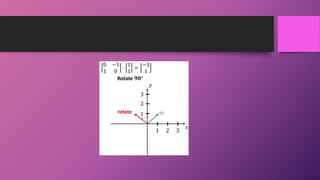
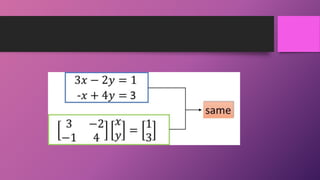
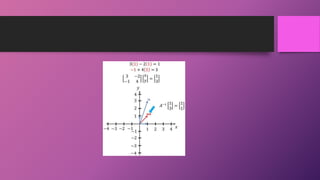
linear algebra for ML

1. Linear Algebra for Machine
Learning basics

2. Why do you need to learn Linear algebra?
• Linear algebra is a foundation of machine learning. Before you
start to study machine learning, you need to get better knowledge
and understanding of this field

3. Vectors, Matrices, and Tensors
• In machine learning, the majority of data is most often
represented as vectors, matrices or tensors. Therefore, the
machine learning heavily relies on the linear algebra.

4. A vector
• A vector is a 1D array. For instance, a point in space can be
defined as a vector of three coordinates (x, y, z). Usually, it is
defined in such a way that it has both the magnitude and the
direction.

5. A matrix
• A matrix is a two-dimensional array of numbers, that has a fixed
number of rows and columns. It contains a number at the
intersection of each row and each column. A matrix is usually
denoted by square brackets [].

7. Tensors
• A tensor is a generalization of vectors and matrices. For instance,
a tensor of dimension one is a vector. In addition, we can also
have a tensor of two dimensions which is a matrix. Then, we can
have a three-dimensional tensor such as the image with RGB
colors. This continues to expand to four-dimensional tensors and
so on.

9. Linear Algebra examples

13. Eigenvector and eigenvalue
• Any vector that is only scaled by a matrix is called
an eigenvector of that matrix. And how much the vector is
scaled we call the eigenvalue.

14. Eigenvector and eigenvalue