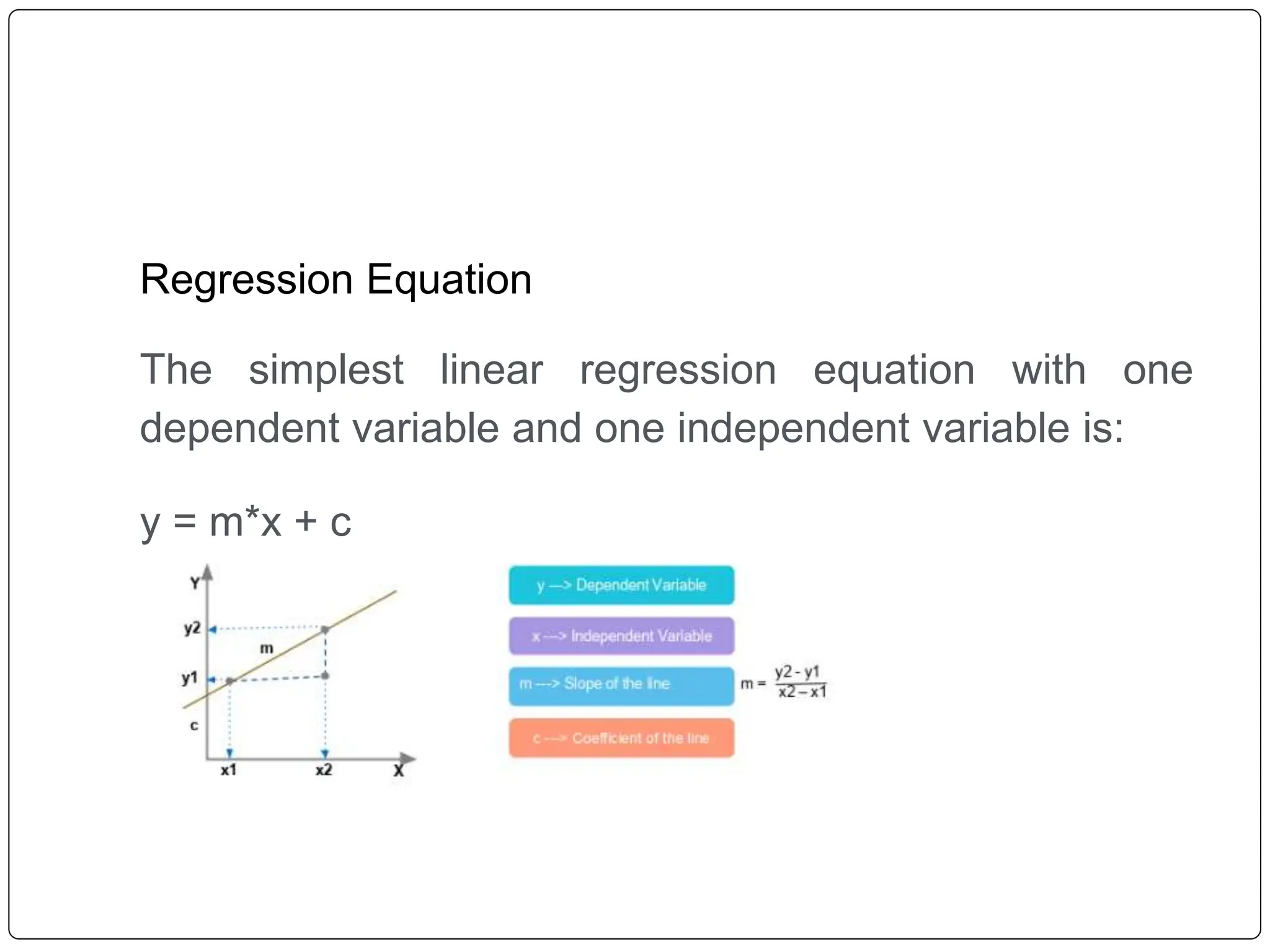
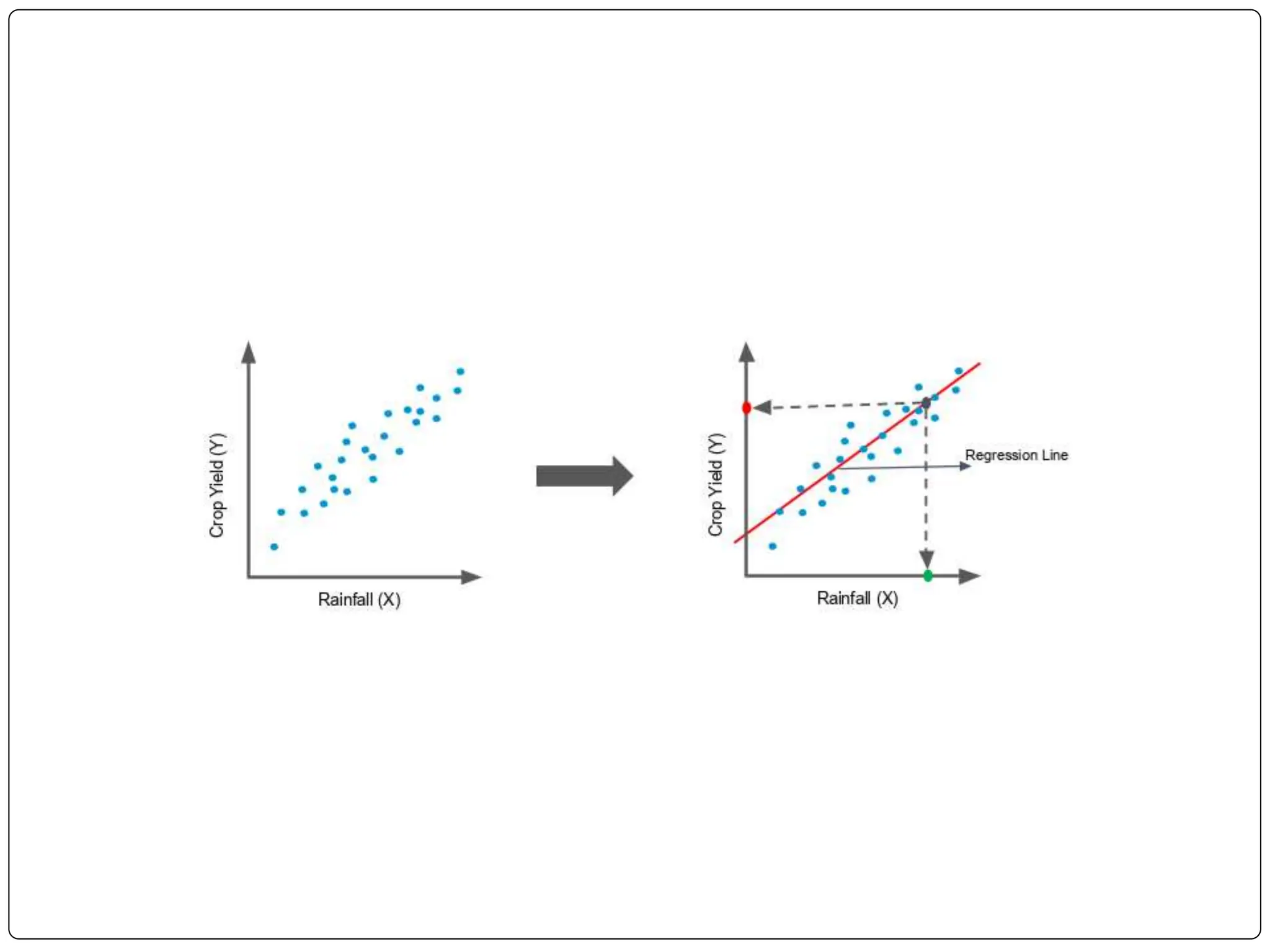
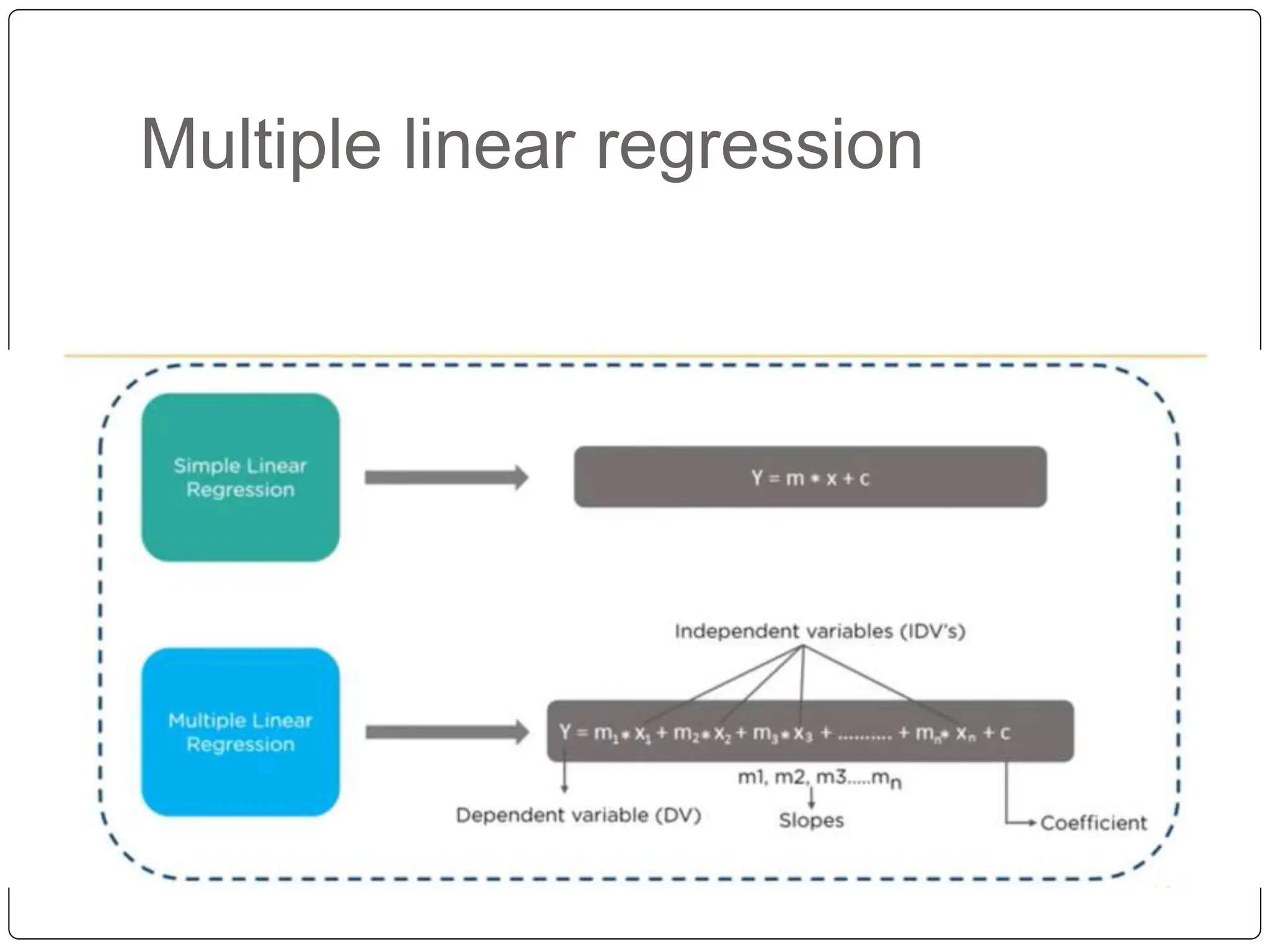
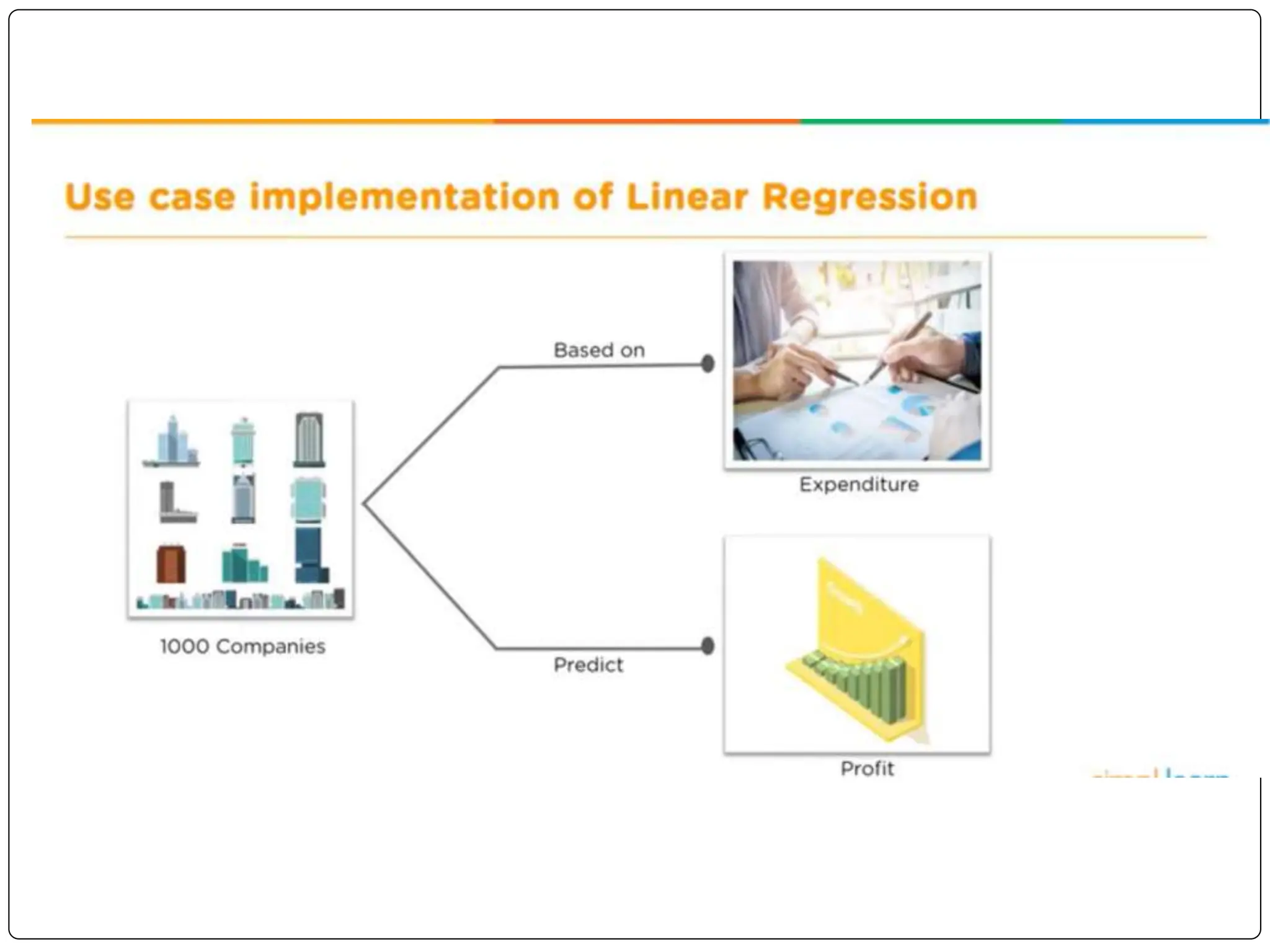
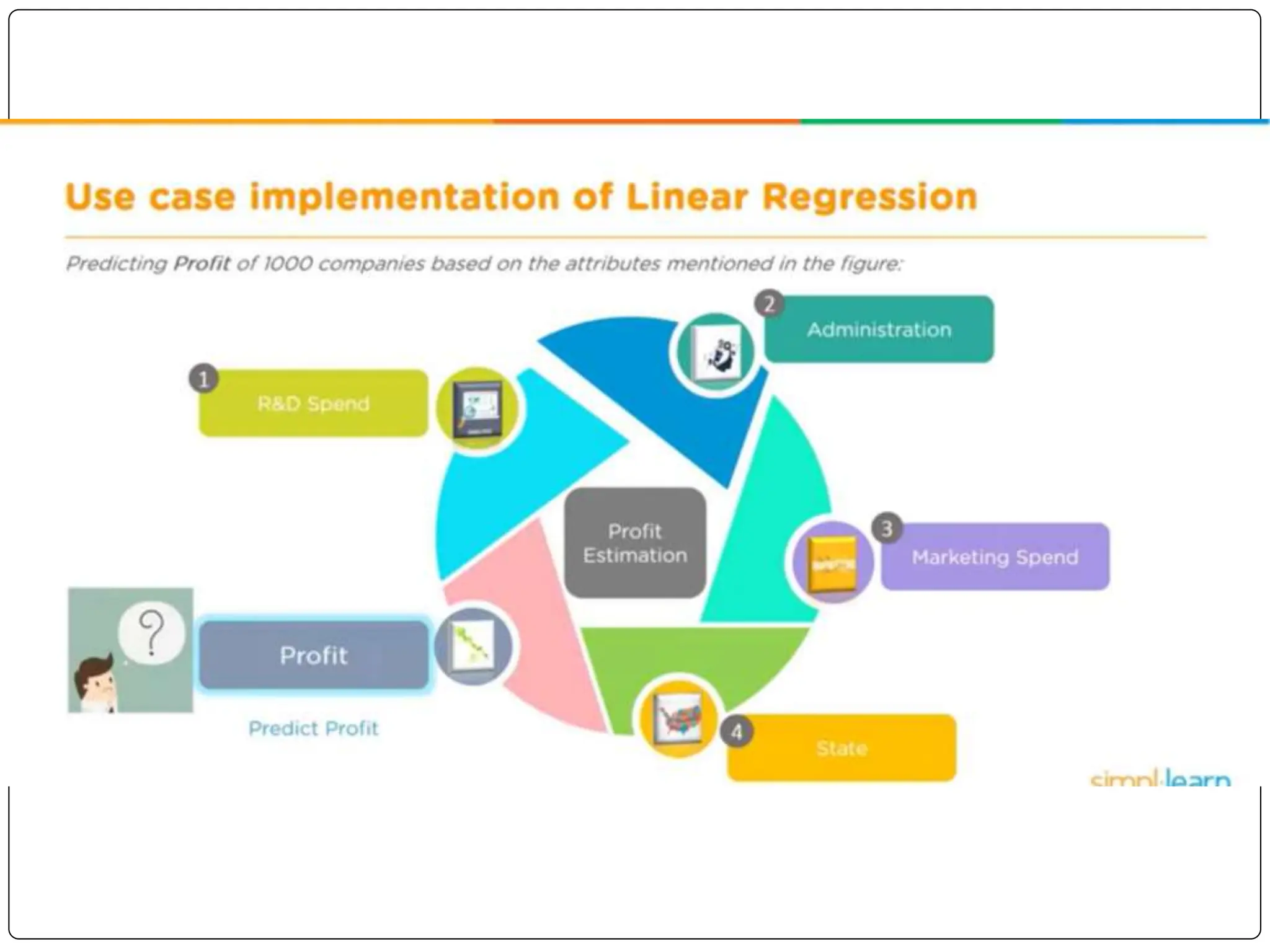
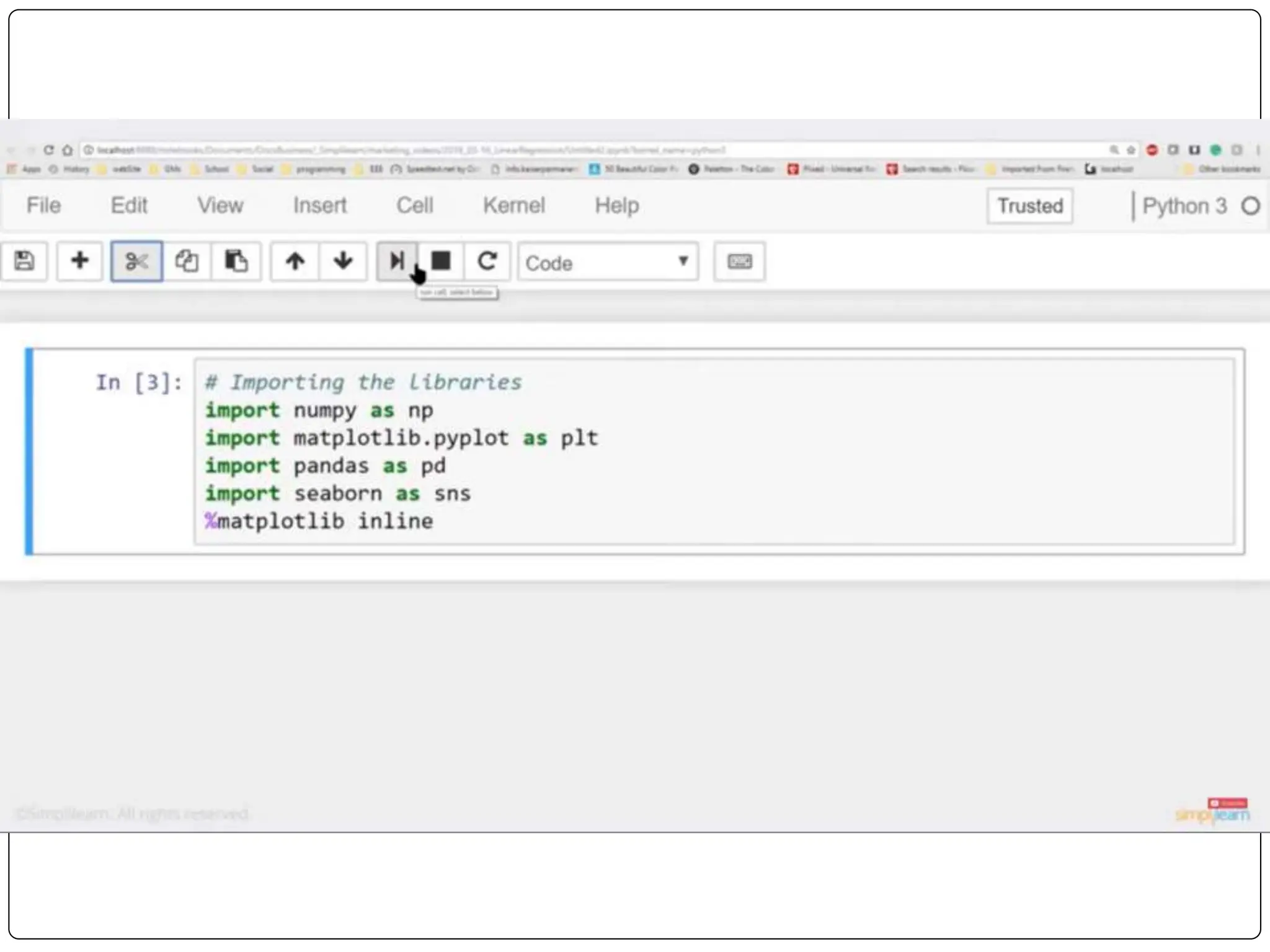
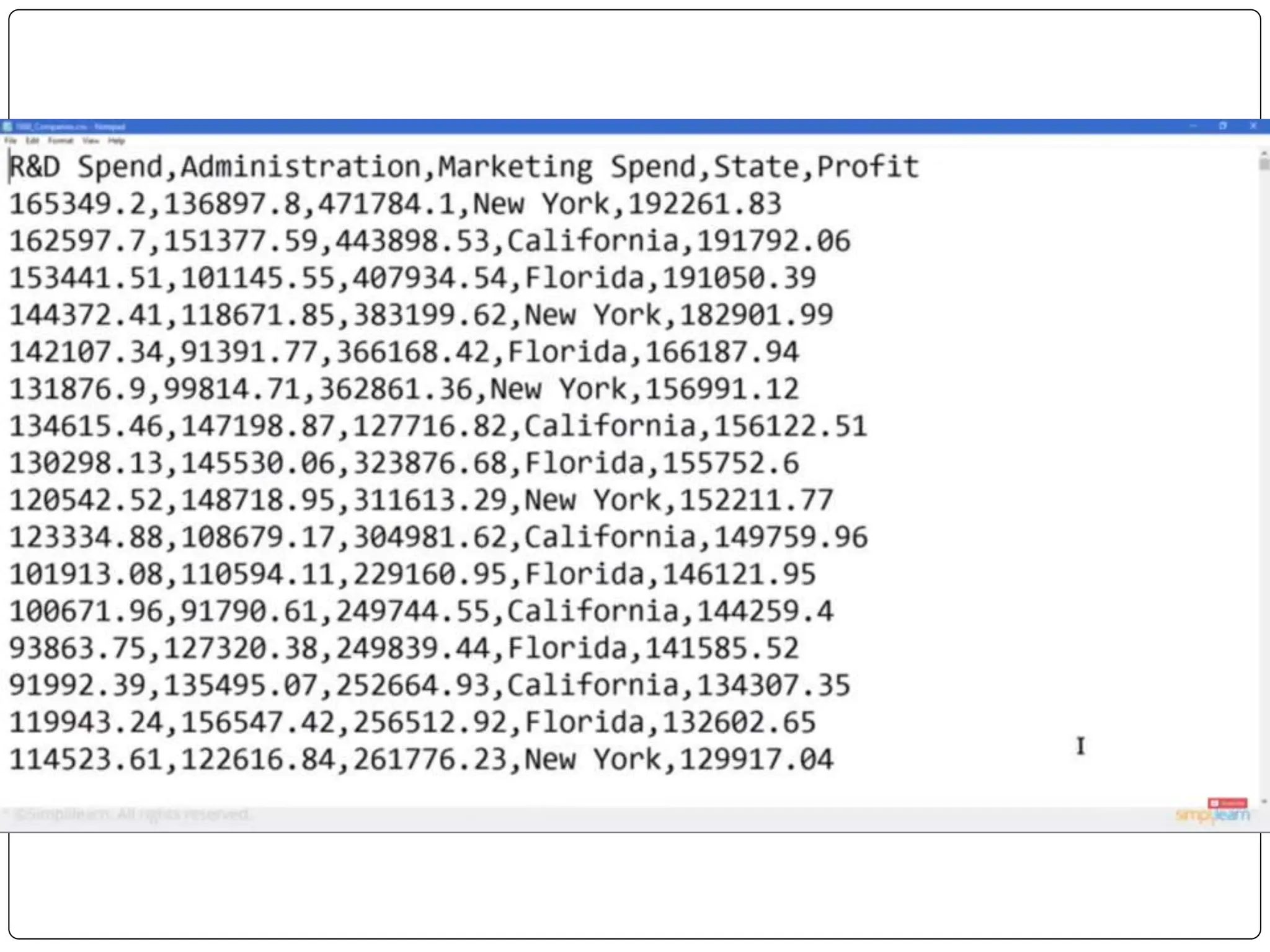
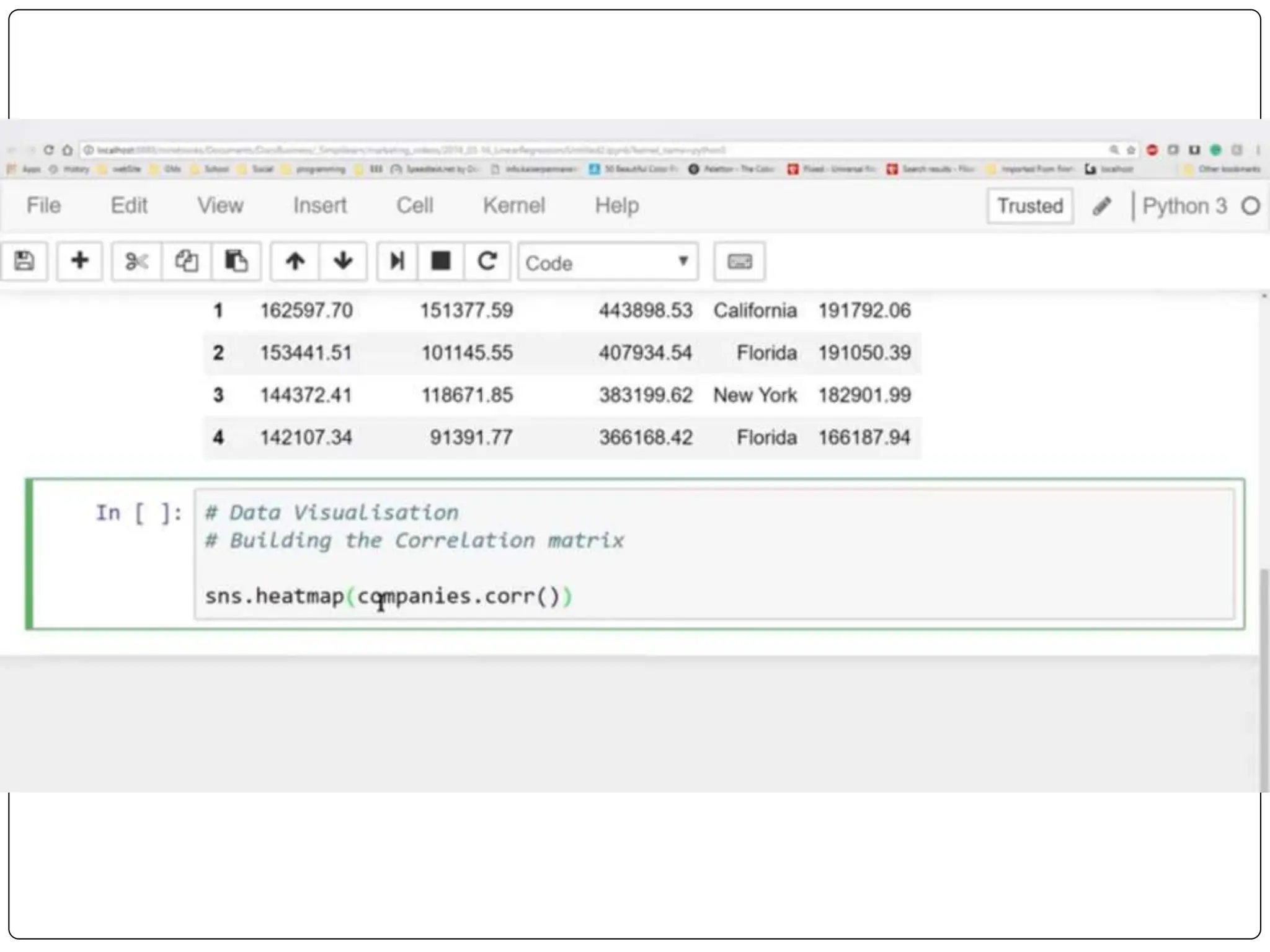
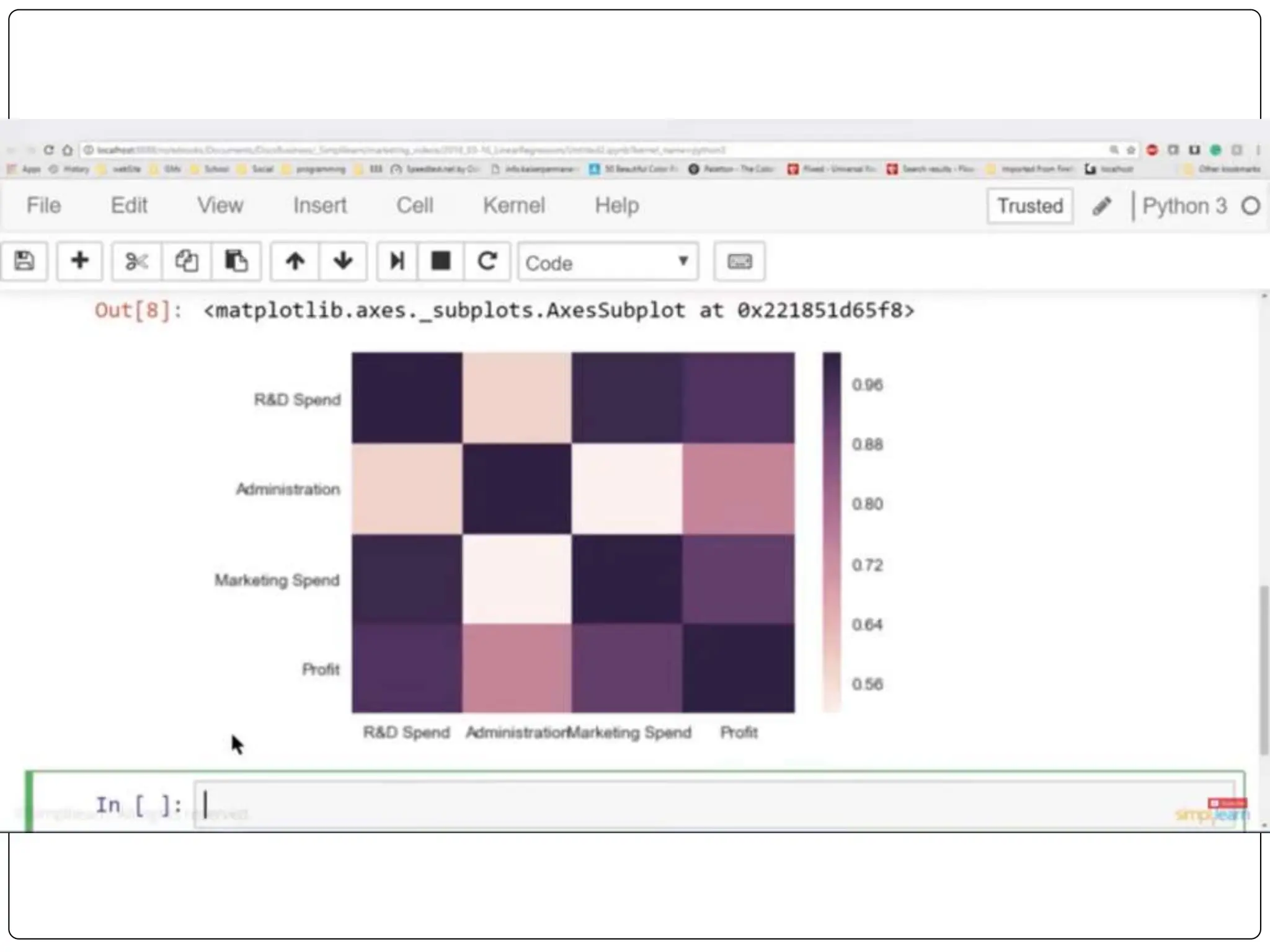
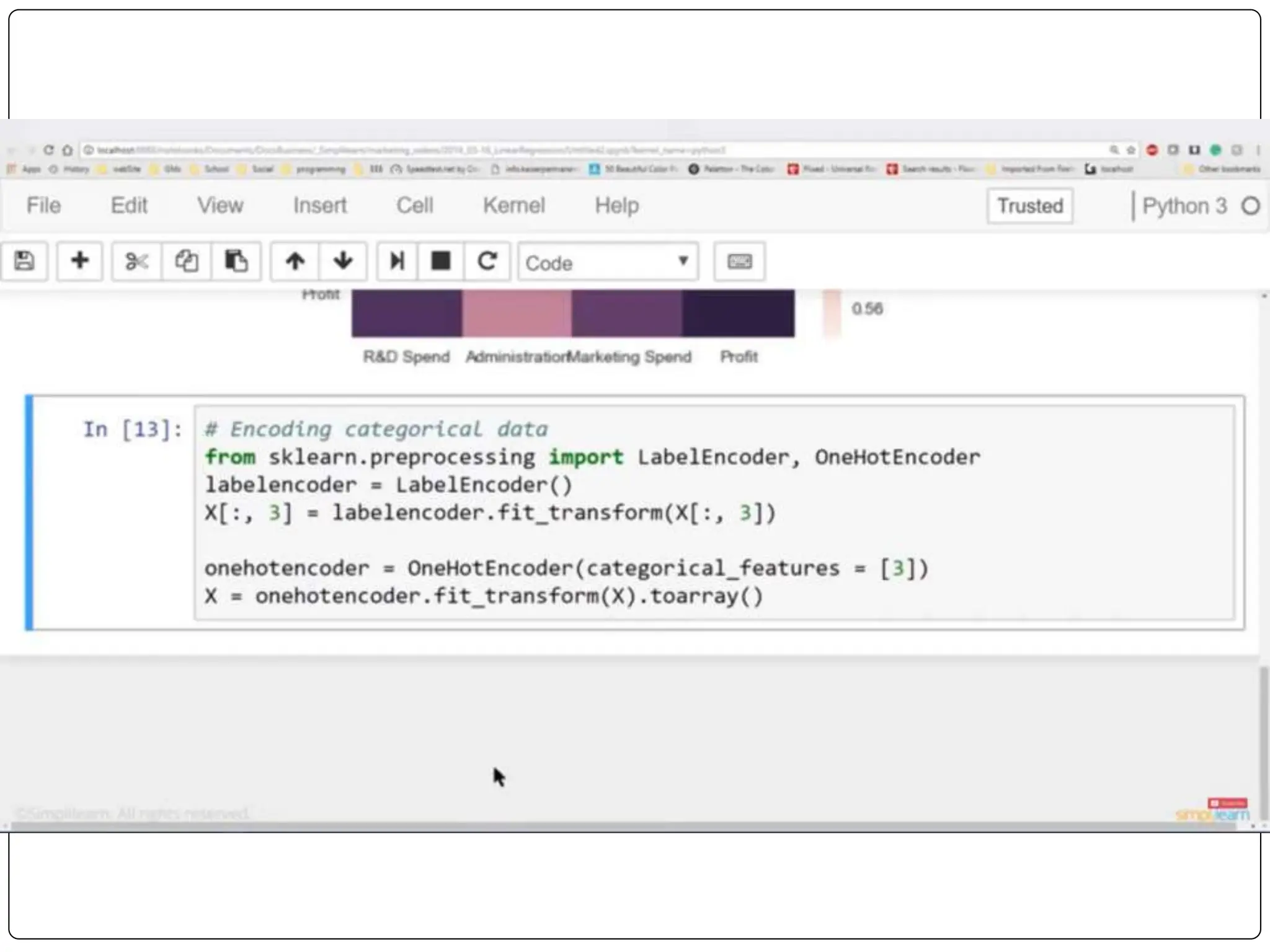
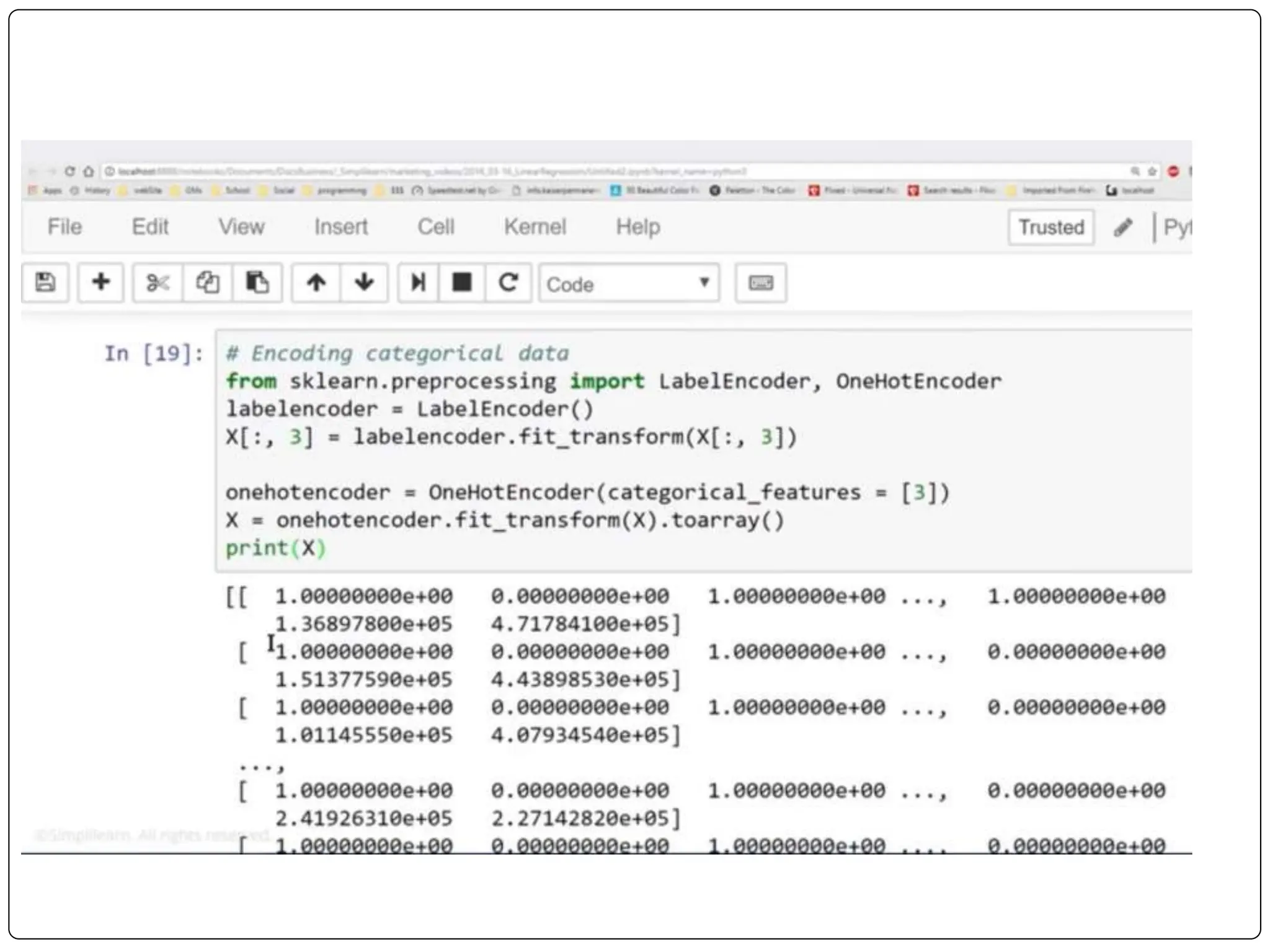
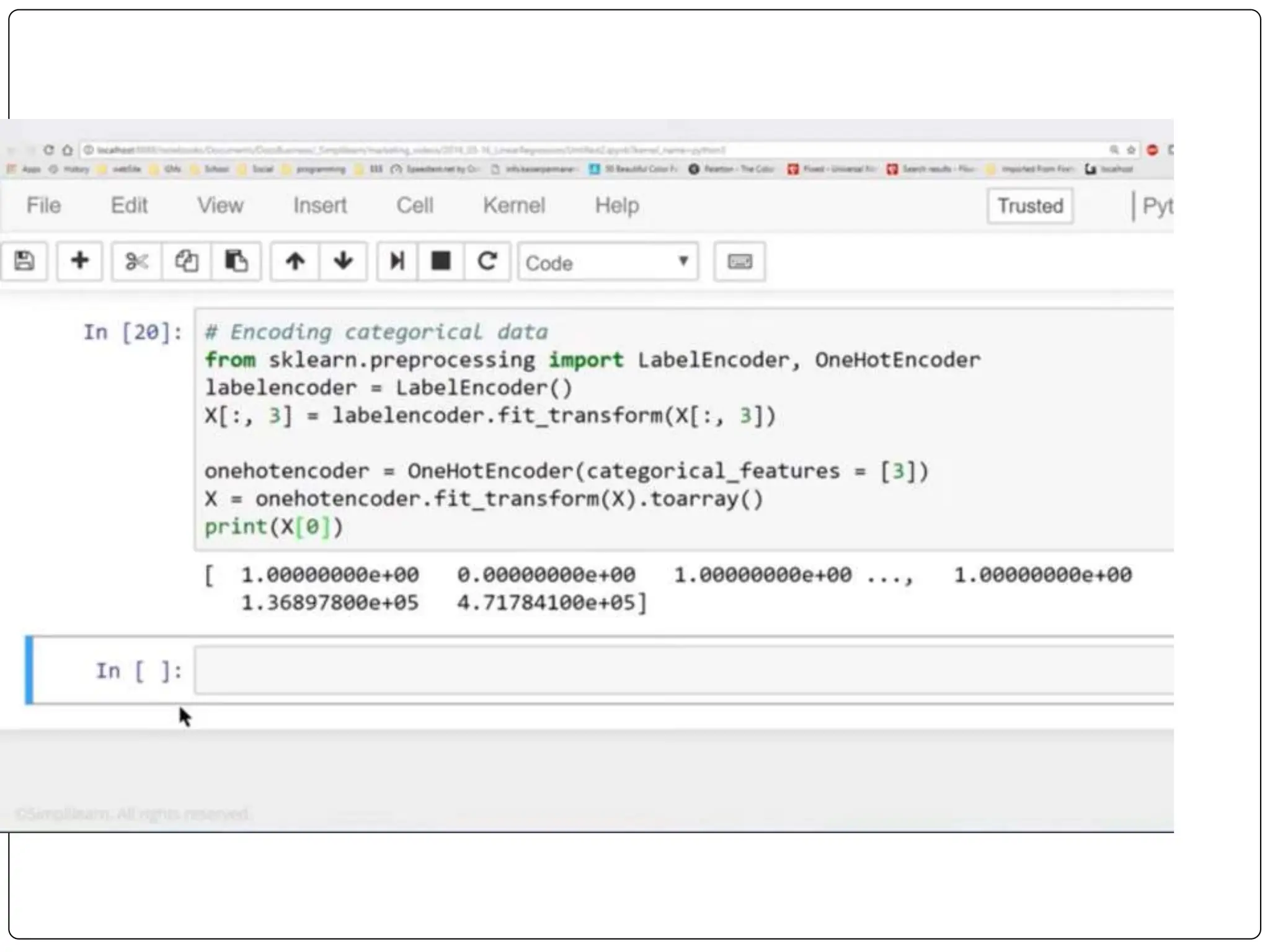
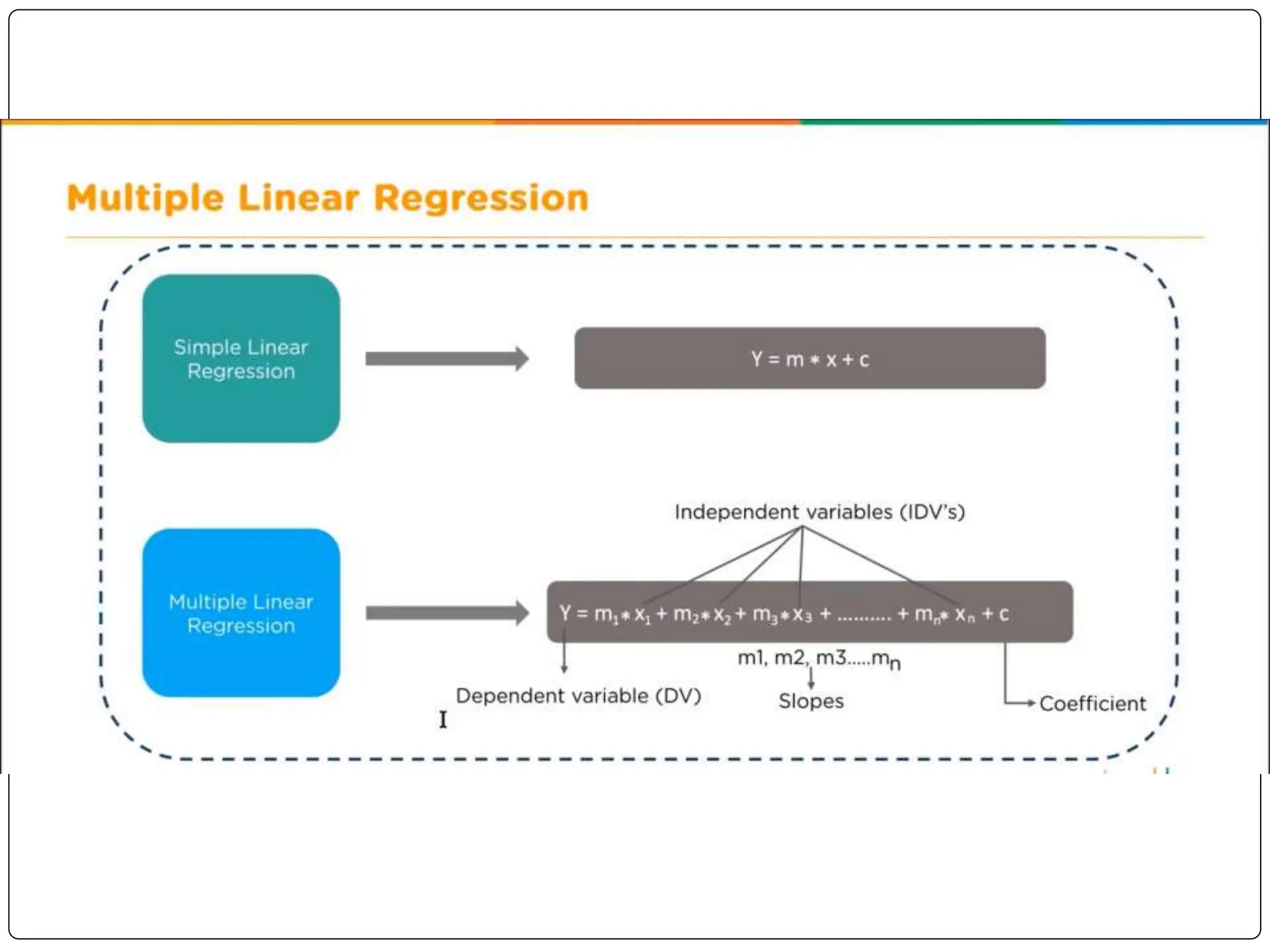
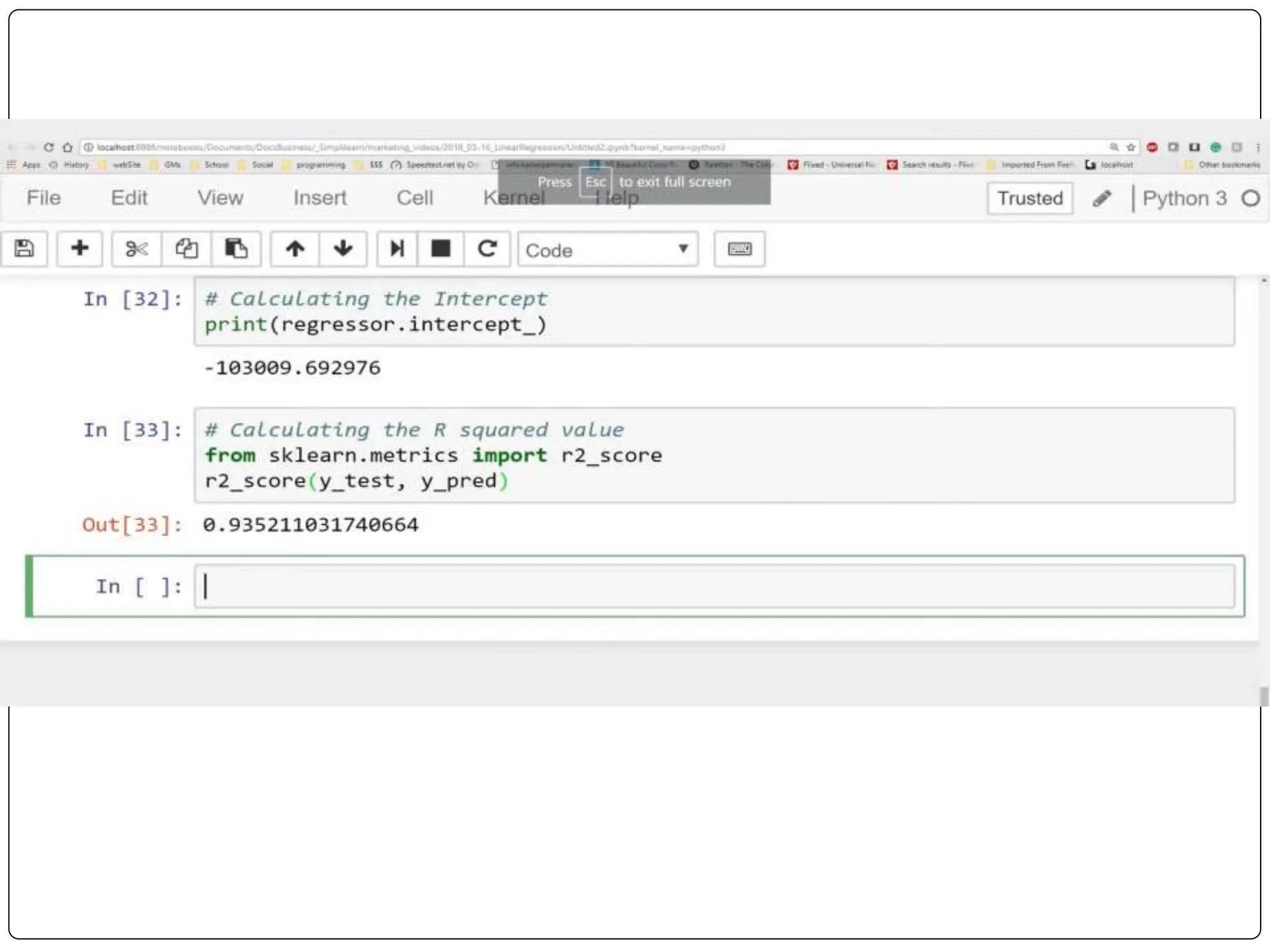
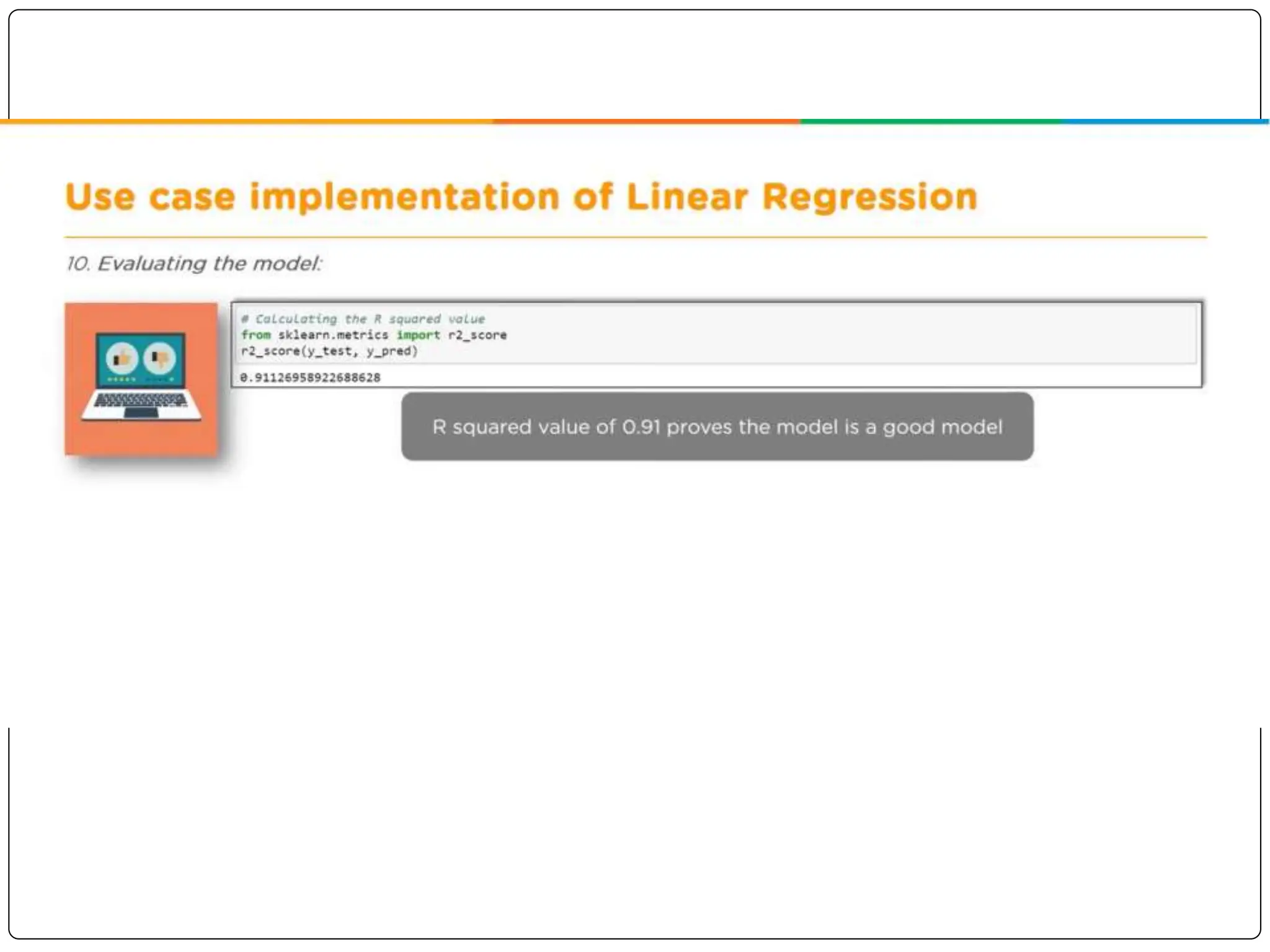
This document discusses multiple linear regression. It begins by explaining linear regression and its applications. It then discusses multiple linear regression, where there is more than one independent variable. As an example, it describes using multiple linear regression to estimate company profits based on various independent variables. The document provides resources for learning more about linear regression in Python.

1. Dr.Sangeetha Vimalraj, SRMIST, Vadapalani
MULTIPLE LINEAR REGRESSION

2. Outline
Dr.Sangeetha Vimalraj, SRMIST, Vadapalani
⚫ Machine learning algorithms
⚫ Applications of linear regression
⚫ Understanding linear regression
⚫ Multiple linear regression
⚫ Use case: profit estimation of companies

3. Machine learning algorithms
Dr.Sangeetha Vimalraj, SRMIST, Vadapalani
The two most common uses for supervised learning
are:
● Regression
● Classification
Regression is divided into three types:
● Simple linear regression
● Multiple linear regression
● Polynomial linear regression

4. Applications of linear
regression
Dr.Sangeetha Vimalraj, SRMIST, Vadapalani
● Economic Growth
● Product Price
● Housing Sales
● Score Predictions

5. Linear regression is a statistical model used to predict
the relationship between independent and dependent
variables by examining two factors:
1. Which variables, in particular, are significant
predictors of the outcome variable?
2. How significant is the regression line in terms of
making predictions with the highest possible
accuracy?

6. Example
Predict future crop yields based on the amount of
rainfall, using data regarding past crops and rainfall
amounts.
⚫ Independent Variable - Rainfall
⚫ Dependent Variable - Crop yield

7. Regression Equation
The simplest linear regression equation with one
dependent variable and one independent variable is:
y = m*x + c

9. EXAMPLE
https://www.simplilearn.com/tutorials/machine-
learning-tutorial/linear-regression-in-python

10. Multiple linear regression

30. https://jupyter.org/

31. 1. In practice, Line of best fit or regression line is found
when _____________
a) Sum of residuals (∑(Y – h(X))) is minimum
b) Sum of the absolute value of residuals (∑|Y-h(X)|) is
maximum
c) Sum of the square of residuals ( ∑ (Y-h(X))2) is
minimum
d) Sum of the square of residuals ( ∑ (Y-h(X))2) is
maximum

32. 1. In practice, Line of best fit or regression line is found
when _____________
a) Sum of residuals (∑(Y – h(X))) is minimum
b) Sum of the absolute value of residuals (∑|Y-h(X)|) is
maximum
c) Sum of the square of residuals ( ∑ (Y-h(X))2) is
minimum
d) Sum of the square of residuals ( ∑ (Y-h(X))2) is
maximum

33. 2. If Linear regression model perfectly first i.e., train
error is zero, then _____________________
a) Test error is also always zero
b) Test error is non zero
c) Couldn’t comment on Test error
d) Test error is equal to Train error

34. 2. If Linear regression model perfectly first i.e., train
error is zero, then _____________________
a) Test error is also always zero
b) Test error is non zero
c) Couldn’t comment on Test error
d) Test error is equal to Train error

35. 3. Which of the following metrics can be used for
evaluating regression models?
i) R Squared
ii) Adjusted R Squared
iii) F Statistics
iv) RMSE / MSE / MAE
a) ii and iv
b) i and ii
c) ii, iii and iv
d) i, ii, iii and iv

36. 3. Which of the following metrics can be used for
evaluating regression models?
i) R Squared
ii) Adjusted R Squared
iii) F Statistics
iv) RMSE / MSE / MAE
a) ii and iv
b) i and ii
c) ii, iii and iv
d) i, ii, iii and iv

37. 4. How many coefficients do you need to estimate in a
simple linear regression model (One independent
variable)?
a) 1
b) 2
c) 3
d) 4

38. 4. How many coefficients do you need to estimate in a
simple linear regression model (One independent
variable)?
a) 1
b) 2
c) 3
d) 4

39. 5. In a simple linear regression model (One
independent variable), If we change the input variable
by 1 unit. How much output variable will change?
a) by 1
b) no change
c) by intercept
d) by its slope

40. 5. In a simple linear regression model (One
independent variable), If we change the input variable
by 1 unit. How much output variable will change?
a) by 1
b) no change
c) by intercept
d) by its slope
Explanation: For linear regression Y=a+bx+error. If neglect error then Y=a+bx. If x increases by
1, then Y = a+b(x+1) which implies Y=a+bx+b. So Y increases by its slope

41. 6. In the mathematical Equation of Linear Regression
Y = β1 + β2X + ϵ, (β1, β2) refers to __________
a) (X-intercept, Slope)
b) (Slope, X-Intercept)
c) (Y-Intercept, Slope)
d) (slope, Y-Intercept)

42. 6. In the mathematical Equation of Linear Regression
Y = β1 + β2X + ϵ, (β1, β2) refers to __________
a) (X-intercept, Slope)
b) (Slope, X-Intercept)
c) (Y-Intercept, Slope)
d) (slope, Y-Intercept)

43. 7.Linear Regression is a supervised machine learning
algorithm. True/False

44. 7.Linear Regression is a supervised machine learning
algorithm. True/False

45. 8. Which of the following methods do we use to find the
best fit line for data in Linear Regression?
A) Least Square Error
B) Maximum Likelihood
C) Logarithmic Loss
D) Both A and B

46. 8. Which of the following methods do we use to find the
best fit line for data in Linear Regression?
A) Least Square Error
B) Maximum Likelihood
C) Logarithmic Loss
D) Both A and B

47. 9. Which of the following is true about Residuals ?
A) Lower is better
B) Higher is better
C) A or B depend on the situation
D) None of these

48. 9. Which of the following is true about Residuals ?
A) Lower is better
B) Higher is better
C) A or B depend on the situation
D) None of these

49. 10. Suppose that we have N independent variables
(X1,X2… Xn) and dependent variable is Y. Now
Imagine that you are applying linear regression by fitting
the best fit line using least square error on this data.
You found that correlation coefficient for one of it’s
variable(Say X1) with Y is -0.95.
Which of the following is true for X1?
A) Relation between the X1 and Y is weak
B) Relation between the X1 and Y is strong
C) Relation between the X1 and Y is neutral
D) Correlation can’t judge the relationship

50. 10. Suppose that we have N independent variables
(X1,X2… Xn) and dependent variable is Y. Now
Imagine that you are applying linear regression by fitting
the best fit line using least square error on this data.
You found that correlation coefficient for one of it’s
variable(Say X1) with Y is -0.95.
Which of the following is true for X1?
A) Relation between the X1 and Y is weak
B) Relation between the X1 and Y is strong
C) Relation between the X1 and Y is neutral
D) Correlation can’t judge the relationship