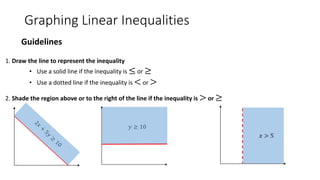
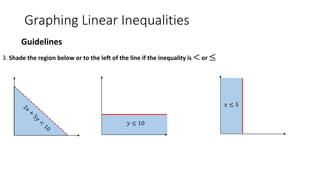
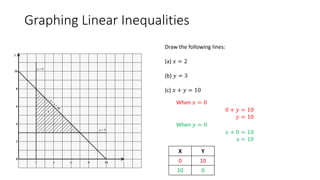
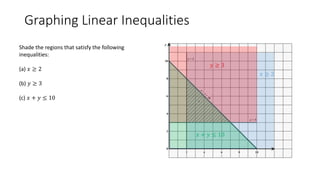
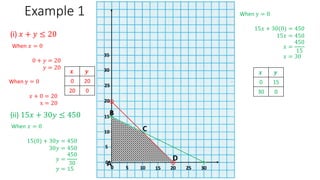
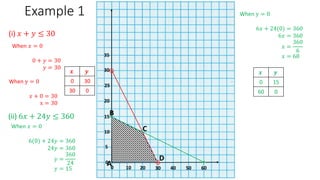
The document discusses linear inequalities and how to graph them on a coordinate plane. It provides guidelines for graphing linear inequalities based on whether the inequality symbol is <, ≤, >, or ≥ and which regions to shade. Several examples are worked through step-by-step to demonstrate how to graph and analyze various linear inequalities.

1. Linear Programming

2. Linear Inequalities
> greater than
≥ greater than or equal to; at least; no less than
< less than
≤ less than or equal to; at most; no more than

3. Graphing Linear Inequalities
Guidelines
2. Shade the region above or to the right of the line if the inequality is > or ≥
1. Draw the line to represent the inequality
• Use a solid line if the inequality is ≤ or ≥
• Use a dotted line if the inequality is < or >
𝑦 ≥ 10
𝑥 > 5

4. Graphing Linear Inequalities
Guidelines
3. Shade the region below or to the left of the line if the inequality is < or ≤
𝑦 ≤ 10
𝑥 ≤ 5

5. Graphing Linear Inequalities
X Y
0 10
10 0
Draw the following lines:
(a) 𝑥 = 2
(b) 𝑦 = 3
(c) 𝑥 + 𝑦 = 10
When 𝑥 = 0
0 + 𝑦 = 10
𝑦 = 10
When 𝑦 = 0
𝑥 + 0 = 10
x = 10

6. Graphing Linear Inequalities
𝑥 ≥ 2
𝑥 + 𝑦 ≤ 10
𝑦 ≥ 3
Shade the regions that satisfy the following
inequalities:
(a) 𝑥 ≥ 2
(b) 𝑦 ≥ 3
(c) 𝑥 + 𝑦 ≤ 10

7. Example 1
(i) 𝑥 + 𝑦 ≤ 20
(ii) 15𝑥 + 30𝑦 ≤ 450

8. Example 1

9. Example 1
5 10 15 20 25 30
0
0
5
10
15
20
25
30
35
(i) 𝑥 + 𝑦 ≤ 20
(ii) 15𝑥 + 30𝑦 ≤ 450
When 𝑥 = 0
0 + 𝑦 = 20
𝑦 = 20
When y = 0
𝑥 + 0 = 20
x = 20
When 𝑥 = 0
15(0) + 30𝑦 = 450
30𝑦 = 450
𝑦 =
450
30
𝑦 = 15
When y = 0
15𝑥 + 30(0) = 450
15𝑥 = 450
𝑥 =
450
15
𝑥 = 30
𝒙 𝒚
0 20
20 0
𝒙 𝒚
0 15
30 0




A
B
C
D

10. Example 1
(iii) A (0, 0)
B (0, 15)
C (10, 10)
D (0, 20)
(b)

11. Example 1
(i) Total profit = 8𝑥 + 20𝑦
(ii) B (0, 15), when 𝑥 = 0 then 𝑦 = 15
𝑇𝑜𝑡𝑎𝑙 𝑝𝑟𝑜𝑓𝑖𝑡 = 8 0 + 20 15 = 0 + 300 = 300
C (10, 10), when 𝑥 = 10 then 𝑦 = 10
𝑇𝑜𝑡𝑎𝑙 𝑝𝑟𝑜𝑓𝑖𝑡 = 8 10 + 20 10 = 80 + 200 = 280
D (0, 20), when 𝑥 = 0 then 𝑦 = 20
𝑇𝑜𝑡𝑎𝑙 𝑝𝑟𝑜𝑓𝑖𝑡 = 8 0 + 20 20 = 0 + 400 = 400
Therefore the maximum profit is $400,
when the pizza shop makes 0 small
pizza and 20 large pizzas.

12. Example 2
(i) 𝑥 + 𝑦 ≤ 30
(ii) 6𝑥 + 24𝑦 ≤ 360

13. Example 2

14. Example 1
10 20 30 40 50 60
0
0
5
10
15
20
25
30
35
When 𝑥 = 0
0 + 𝑦 = 30
𝑦 = 30
When y = 0
𝑥 + 0 = 30
x = 30
When 𝑥 = 0
6(0) + 24𝑦 = 360
24𝑦 = 360
𝑦 =
360
24
𝑦 = 15
When y = 0
6𝑥 + 24(0) = 360
6𝑥 = 360
𝑥 =
360
6
𝑥 = 60
𝒙 𝒚
0 30
30 0
𝒙 𝒚
0 15
60 0




A
B
C
D
(i) 𝑥 + 𝑦 ≤ 30
(ii) 6𝑥 + 24𝑦 ≤ 360

15. Example 2
(b)
(iii) A (0, 0)
B (0, 15)
C (20, 10)
D (30, 0)

16. Example 2
(i) P = 𝑥 + 3𝑦
B (0, 15), when 𝑥 = 0 then 𝑦 = 15
𝑃 = 1 0 + 3 15 = 0 + 45 = 45
C (20, 10), when 𝑥 = 20 then 𝑦 = 10
𝑃 = 1 20 + 3 10 = 20 + 30 = 50
D (30, 0), when 𝑥 = 30 then 𝑦 = 0
𝑃 = 1 30 + 3 0 = 30 + 0 = 30
(ii) Therefore the maximum profit that may
be made is $50, when 20 balls and 10 bats
are sold

17. Example 3

18. Example 3

19. Example 3