The document discusses probabilistic models for sequence data, including Markov models and hidden Markov models (HMMs). It introduces the key concepts of Markov models, including the state transition matrix and parameter estimation using maximum likelihood. For HMMs, it describes the generative process, inference algorithms like forward-backward, Viterbi, and parameter estimation using the Baum-Welch algorithm. The document provides an overview of these fundamental probabilistic models for sequential data.

1. Probabilistic Models
for Sequence Data
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 1

2. Random Sequence Data
• 𝑋1, 𝑋2, … , 𝑋𝑇
• Subscript denotes steps in “time”
• Many applications
• NLP, “Arrival” data, Weather, Stocks, Biology, …
• Naïve models
• Complete independence – too simple
• Complete pairwise dependence – too many parameters
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 2

3. Markov Model
• 𝑃(𝑋1: 𝑇) = 𝑃(𝑋1)(𝑃𝑋2|𝑋1) … 𝑃(𝑋𝑇−1|𝑋𝑇)
• Markov (conditional independence) assumption
• 𝑋𝑡+1 ⋮ 𝑋𝑡−𝑖 | 𝑋𝑡 for all 𝑖
• Future conditionally independent of past given present
• Still too many parameters
• Homogeneous / stationary: 𝑃(𝑋𝑡+1|𝑋𝑡) is same for all 𝑡
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 3
𝑋1 𝑋2 𝑋𝑇−1 𝑋𝑇

4. State Transition Matrix
• For discrete 𝑋𝑖
• State transition matrix 𝐴
• 𝐴𝑖𝑗 = 𝑃(𝑋𝑡+1 = 𝑗|𝑋𝑡 = 𝑖)
• Stochastic matrix
• N-step matrix 𝐴(𝑛)
• 𝐴𝑖𝑗(𝑛) = 𝑃(𝑋𝑡+𝑛 = 𝑗|𝑋𝑡 = 𝑖)
• Chapman Kolmogorov Equation
• 𝐴𝑖𝑗(𝑚 + 𝑛) = 𝑘 𝐴𝑖𝑘 𝑚 𝐴𝑘𝑗(𝑛)
• 𝐴(𝑚 + 𝑛) = 𝐴(𝑚)𝐴(𝑛)
• 𝐴(𝑛) = 𝐴𝑛
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 4

5. MLE for a Markov Chain
• Data: Multiple sequences
• 𝐷 = {𝑥1, … , 𝑥𝑁}, where 𝑥𝑖 = {𝑥𝑖1, … 𝑥𝑖𝑇𝑖
}
• Formulate loglikelihood
𝑖
𝑝 𝑥𝑖1
𝑗
𝑝(𝑥𝑖𝑗|𝑥𝑖𝑗−1) =
𝑗
𝜋𝑗
𝑁𝑗
1
𝑖𝑗
𝐴𝑖𝑗
𝑁𝑖𝑗
where 𝑁𝑗
1
, 𝑁𝑖𝑗 denote …
• Maximize wrt parameters
𝜋𝑗 =
𝑁𝑗
1
𝑗 𝑁𝑗
1 𝐴𝑖𝑗 =
𝑁𝑖𝑗
𝑗 𝑁𝑖𝑗
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 5

6. Digression: Stationary Distribution
• Does a Markov Chain ever stabilize, ie 𝜋𝑡+1 = 𝜋𝑡?
• Only if A satisfies particular properties
• Ergodic Markov Chains
• Without Ergodic Markov Chains our daily lives would
come to a standstill …
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 6

7. Hidden Markov Model
• Sequence over discrete states
• States generate emissions
• Emissions are observed, but states are hidden
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 7

8. Motivations
• States have physical “meaning”
• Speech recognition
• Speaker diaritization
• Part of speech tagging
• …
• Long range dependencies in Markov Model with a
few parameters
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 8

9. Hidden Markov Model
• Conditional Independence assumptions
𝑍𝑡+1 ⋮ 𝑍𝑡−1| 𝑍𝑡
𝑋𝑡 𝑍𝑡
′
, 𝑋𝑡
′′
𝑍𝑡
• Likelihood
𝑃 𝑍, 𝑋 = 𝑃 𝑍1 𝑃 𝑋1 𝑍1
𝑡
𝑃 𝑍𝑡 𝑍𝑡−1 𝑃(𝑋𝑡|𝑍𝑡)
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 9

10. Hidden Markov Model: Generative Process
1. Sample an initial state 𝑍1 ∼ 𝑝(𝑧1)
2. Sample an initial output from initial state: 𝑋1 ∼ 𝑝(𝑥1|𝑧1)
3. Repeat for N steps
4. Sample curr state based on prev. state 𝑍𝑡 ∼ 𝑝(𝑧𝑡|𝑧𝑡−1)
5. Sample curr output based on curr state 𝑋𝑡 ∼ 𝑝(𝑥𝑡|𝑧𝑡)
• Compare with iid generative mixture models
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 10

11. Inference Problems
• Filtering
𝑃(𝑧𝑡|𝑥1:𝑡)
• Smoothing
𝑃(𝑧𝑡−𝑙|𝑥1:𝑡) for 𝑙 = 1,2, …
• Prediction
𝑃 𝑥𝑡+ℎ 𝑥1:𝑡 for ℎ = 1,2, …
• MAP estimation / Viterbi decoding
arg max
𝑧
𝑃(𝑧1:𝑇|𝑥1:𝑇)
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 11

12. Inference: Challenge
• Naïve summation does not work
𝑝 𝑧𝑡 𝑥 =
𝑧−𝑡
𝑝(𝑧1, 𝑧2, … , 𝑧𝑡, … , 𝑧𝑇, 𝑥1, 𝑥2, … , 𝑥𝑇)
𝑧1,…,𝑧𝑇
𝑝(𝑧1, 𝑧2, … , 𝑧𝑡, … , 𝑧𝑇, 𝑥1, 𝑥2, … , 𝑥𝑇)
• What is the cost?
• Solution: Identify and reuse shared computations
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 12

13. Forward Algorithm
Define 𝛼𝑡 𝑗 ≡ 𝑝 𝑧𝑡 = 𝑗 𝑥1:𝑡
= 𝑝 𝑧𝑡 = 𝑗 𝑥𝑡, 𝑥1:𝑡−1
∝ 𝑝 𝑥𝑡 𝑧𝑡 = 𝑗 𝑝 𝑧𝑡 = 𝑗 𝑥1:𝑡−1 (Derivation? Normalization?)
= 𝑝 𝑥𝑡 𝑧𝑡 = 𝑗
𝑖
𝑝 𝑧𝑡 = 𝑗 𝑧𝑡−1 = 𝑖 𝑝(𝑧𝑡−1 = 𝑖|𝑥1:𝑡−1)
= 𝜓𝑡(𝑗)
𝑖
𝐴(𝑗, 𝑖)𝛼𝑡−1(𝑖)
• Simple recursive algorithm
• Base case: 𝛼0 𝑗 = 𝜓0 𝑗 𝜋𝑗
• Complexity 𝑂(𝐾2
𝑇) where K is #state values
• Compare with iid models
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 13

14. Backward Algorithm
Define 𝛽𝑡 𝑗 ≡ 𝑝 𝑥𝑡+1:𝑇 𝑧𝑡 = 𝑗
=
𝑖
𝑝 𝑧𝑡+1 = 𝑖, 𝑥𝑡+1, 𝑥𝑡+2:𝑇 |𝑧𝑡 = 𝑗)
=
𝑖
𝑝 𝑥𝑡+2:𝑇 𝑧𝑡+1 = 𝑖 𝑝(𝑧𝑡+1 = 𝑖, 𝑥𝑡+1|𝑧𝑡 = 𝑗)
=
𝑖
𝑝 𝑥𝑡+2:𝑇 𝑧𝑡+1 = 𝑖 𝑝 𝑥𝑡+1 𝑧𝑡+1 = 𝑖 𝑝 𝑧𝑡+1 = 𝑖 𝑧𝑡 = 𝑗
=
𝑖
𝛽𝑡+1 𝑖 𝜓𝑡+1 𝑖 𝐴(𝑗, 𝑖)
• Simple recursive algorithm
• Base case?
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 14

15. Forward Backward Algorithm
Define 𝛾𝑡 𝑗 = 𝑝 𝑧𝑡 = 𝑗 𝑥1:𝑇
∝ 𝛼𝑡 𝑗 𝛽𝑡(𝑗)
• Overall algorithm
• Compute forward pass
• Compute backward pass
• Combine to get 𝛾𝑡 𝑗
• Sum product algorithm
• Belief propagation / message passing algorithm
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 15

16. Viterbi Algorithm
• Most likely sequence of states
𝑧∗ = arg max
𝑧1:𝑇
𝑝(𝑧1:𝑇|𝑥1:𝑇)
• Not the same as sequence of most likely states
arg max
𝑧1
𝑝(𝑧1|𝑥1:𝑇) , arg max
𝑧2
𝑝(𝑧2|𝑥1:𝑇),…, arg max
𝑧𝑇
𝑝(𝑧𝑇|𝑥1:𝑇)
• Forward Backward + additional bookkeeping
• Track “trellis” of states
• Max product algorithm
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 16

17. Parameter Estimation
• Straight forward for fully observed data
• Homework
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 17

18. EM for HMMs (Baum Welch Algorithm)
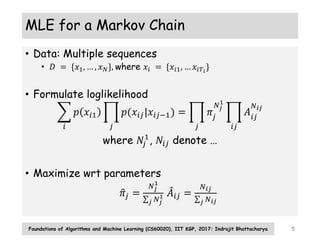
• Formulate complete data loglikelihood
𝑙 Θ
=
𝑘
𝑁𝑘
1
log 𝜋𝑘 +
𝑗 𝑗′
𝑁𝑗𝑗′ log 𝐴𝑗𝑗′
+
𝑖 𝑡 𝑘
𝛿 𝑧𝑡, 𝑘 log 𝑝(𝑥𝑖𝑡|𝜙𝑘)
• Formulate expectation given current parameters
𝑄 Θ, 𝜃𝑜𝑙𝑑
=
𝑘
𝐸[𝑁𝑘
1
] log 𝜋𝑘 +
𝑗 𝑗′
𝐸[𝑁𝑗𝑗′] log 𝐴𝑗𝑗′
+
𝑖 𝑡 𝑘
𝑝 𝑧𝑡 = 𝑘|𝑥𝑖𝑡 log 𝑝(𝑥𝑖𝑡|𝜙𝑘)
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 18

19. E-step
• Compute the current expectations
𝐸 𝑁𝑘
1
=
𝑖
𝑝(𝑧𝑖1 = 𝑘|𝑥𝑖, 𝜃𝑜𝑙𝑑)
Use backward algorithm
𝐸 𝑁𝑗𝑘 =
𝑖 𝑡
𝑝(𝑧𝑖,𝑡−1 = 𝑗, 𝑧𝑖,𝑡 = 𝑘|𝑥𝑖, 𝜃𝑜𝑙𝑑)
Use extension of forward-backward (HW)
𝐸 𝑁𝑘 =
𝑖 𝑡
𝑝(𝑧𝑖,𝑡 = 𝑘|𝑥𝑖, 𝜃𝑜𝑙𝑑)
Use forward-backward
• Compare with iid models
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 19

20. M-step
• Maximize expected complete loglikelihood using
current expected sufficient statistics
𝐴𝑗𝑘 =
𝐸 𝑁𝑗𝑘
𝑘′ 𝐸[𝑁𝑗𝑘′]
𝜋𝑘 =
𝐸 𝑁𝑘
1
𝑁
• Emission parameter estimates depend on emission
distribution
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 20

21. Choosing number of hidden states
• Similar to choosing number of components in
mixture model
• One possibility: Cross validation
• Computationally more costly
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 21

22. Many, many generalizations ….
• Work horse of signal processing, e.g. speech for
decades
• Continuous data
• Long range dependencies
• Multiple hidden layers
• Handling inputs
• …
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 22

23. Linear Chain Conditional Random Fields
• Discriminative Markov Model (recall NB vs LR)
𝑝 𝑧 𝑥 =
1
𝑍(𝑥)
𝑡
exp
𝑘
𝜃𝑘𝑓𝑘(𝑧𝑡, 𝑧𝑡−1,𝑥𝑡)
Where 𝑍 𝑥 = 𝑧 𝑡 exp 𝑘 𝜃𝑘𝑓𝑘(𝑧𝑡, 𝑧𝑡−1,𝑥𝑡)
• Forward backward algorithm for inference
• Gradient descent instead of EM for par estimation
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 23

24. State Space Models
• HMM with continuous hidden states
• Linear dynamical systems
• Conditional distributions are linear-Gaussian
• Mathematically tractable inference
• Kalman filter
• Widely used in time-series analysis + forecasting,
object tracking, robotics, etc
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 24

25. Probabilistic Graphical Models
• Used for modelling conditional independences in
joint distributions using large no. of RVs
• Directed Graphical Models / Bayes Nets
• Undirected Graphical Models / Random Fields
• Inference computationally hard in general
• Parameter estimation with hidden variables harder
• Probability theory + graph theory
Foundations of Algorithms and Machine Learning (CS60020), IIT KGP, 2017: Indrajit Bhattacharya 25