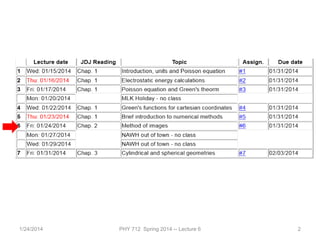
This document outlines the plan for Lecture 6 of a graduate level electromagnetism course. The lecture will continue discussing Chapter 2 and cover methods of images for solving electrostatics problems, including the planar and spherical cases. It will also survey techniques for analyzing the Poisson equation such as direct integration, Green's functions, orthogonal expansions, and the method of images. Several examples are provided of applying these techniques to problems involving different surface geometries like planes, spheres, and cylinders.

1. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 1
PHY 712 Electrodynamics
10-10:50 AM MWF Olin 107
Plan for Lecture 6:
Continue reading Chapter 2
1. Methods of images -- planes,
spheres
2. Solution of Poisson equation in
for other geometries -- cylindrical

2. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 2

3. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 3
Survey of mathematical techniques for analyzing
electrostatics – the Poisson equation
0
2 )
(
)
(

 r
r 



1. Direct integration of differential equation
2. Green’s function techniques
3. Orthogonal function expansions
4. Method of images

4. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 4
Method of images
Clever trick for specialized geometries:
 Flat plane (surface)
 Sphere
Planar case:
Consider a grounded
metal sheet, a distance d
from a point charge q.
d
q

5. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 5
A grounded metal sheet, a distance d from a point charge q.
d
q
Mobile charges from the
“ground” respond to the
force from the charge q.
0
)
,
,
0
( 

 z
y
x
x
z
y

6. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 6
A grounded metal sheet, a distance d from a point charge q.
 
  0
,
,
0
ˆ
3
0
2








z
y
x
d
q
x
r


 
   
  






























2
/
3
2
2
2
0
0
0
2
4
,
,
0
,
,
0
:
density
charge
Surface
ˆ
ˆ
4
1
,
,
0
:
0
for
Trick
z
y
d
d
q
dx
z
y
d
z
y
E
σ(y,z)
d
q
d
q
z
y
x
x



 x
r
x
r

7. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 7
A grounded metal sheet, a distance d from a point charge q.
 
 
q
u
d
udu
d
q
σ(y,z)
dydz
z
y
d
d
q
σ(y,z)




















0
2
/
3
2
2
2
/
3
2
2
2
2
4
2
:
Note
2
4
:
density
charge
Surface



d
q
σ(y,z)

8. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 8
A grounded metal sheet, a distance d from a point charge q.
d
q  
 2
0
2
2
/
3
2
2
2
2
4
ˆ
:
sheet
and
charge
between
Force
2
4
:
density
charge
Surface
d
q
z
y
d
d
q
σ(y,z)


x
F














 
x
q
x
V
x
4
4
)
(
:
distance
at
sheet
and
charge
between
potential
Image
0
2




9. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 9
A grounded metal sphere of radius a, in the presence of a
point charge q at a distance d from its center.
r
d
q
a
  














2
2
0
4
1
:
for
Trick
d
a
a
d
q
q
a
r
a
r
d
r
d
r


10. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 10
A grounded metal sphere of radius a, in the presence of a
point charge q at a distance d from its center.
r
d
q
a
 
 
  2
/
3
0
ˆ
ˆ
2
1
1
4
ˆ
:
density
charge
Surface
2
2
2
2
d
r
r











 d
a
d
a
d
a
a
r d
a
q
r 



11. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 11
A grounded metal sphere of radius a, in the presence of a
point charge q at a distance d from its center.
r
d
q
a
 
 
  2
/
3
0
ˆ
ˆ
2
1
1
4
ˆ
:
density
charge
Surface
2
2
2
2
d
r
r











 d
a
d
a
d
a
a
r d
a
q
r 


 2
2
2
0
2
4
:
q
and
sphere
between
Force
a
d
ad
q



F

12. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 12
Use of image charge formalism to construct Green’s function
   
   
 
'
1
'
1
'
,
:
For
'
4
'
,
0
:
radius
of
sphere
a
on
problem
alue
boundary v
Dirichlet
a
have
we
Suppose
:
Example
2
2
'
'
3
2
0
2
r
r
r
r
r
r
r
r
r
r
r
r
a
a
r
G
a
r,r'
G
a
r
Φ
a




















13. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 13
Solution of the Poisson/Laplace equation in various
geometries -- cylindrical geometry with no z-dependence
(infinitely long wire, for example):

f
   
      )
sin(
ln
B
A
,
:
s
coordinate
in these
equation
Laplace
the
of
solution
General
2
,
,
0
1
1
0
:
equation
Laplace
of
solution
from
functions
orthogonal
ing
Correspond
1
0
0
2
2
2
2




































m
m
m
m
m
m m
B
A
m

f



f


f

f

f






14. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 14
Solution of the Poisson/Laplace equation in various
geometries -- cylindrical geometry with no z-dependence
(infinitely long wire, for example):

f
   
   
 
'
cos
1
2
ln
)
'
,
,
'
,
'
'
4
)
'
,
,
'
,
1
1
:
and
0
at
conditions
boundary
ith
geometry w
for this
e
appropriat
function
s
Green'
1
2
2
2
2
f
f



f
f


f
f






f
f


f



















































 

 m
m
G(
G(
m
m

15. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 15
Solution of the Poisson/Laplace equation in various
geometries -- cylindrical geometry with z-dependence

f
   
       
z
Z
Q
R
z
z
m
z
z
f

f


f

f

f




































,
,
,
2
,
,
,
0
1
1
0
:
equation
Laplace
of
solution
from
functions
orthogonal
ing
Correspond
2
2
2
2
2
2
z

16. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 16
Cylindrical geometry continued:
   
kρ
N
kρ
J
R
m
k
d
dR
d
R
d
e
Q
Q
m
d
Q
d
e
kz
kz
z
Z
Z
k
dz
Z
d
m
m
im
kz
,
0
1
)
(
0
),
cosh(
),
sinh(
)
(
0
2
2
2
2
2
2
2
2
2
2
2



























f
f
f

17. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 17
Cylindrical geometry example:
 
 







m
n
mn
mn
mn
m
mn m
z
k
k
J
A
z
z
V
L
z
,
sin
)
sinh(
)
(
)
,
,
(
boundaries
other
all
on
0
)
,
,
(
)
,
(
)
,
,
(

f

f

f

f

f


18. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 18
Cylindrical geometry example:
 
 



















m
n
mn
m
mn m
L
z
n
L
n
I
A
z
z
z
V
z
a
,
sin
sin
)
,
,
(
boundaries
other
all
on
0
)
,
,
(
)
,
(
)
,
,
(

f


f

f

f
f


19. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 19
Comments on cylindrical Bessel functions
)
(
),
(
)
(
)
(
)
(
)
(
),
(
),
(
)
(
0
)
(
1
1
2
2
2
2
u
K
u
I
u
F
u
N
u
J
u
H
u
N
u
J
u
F
u
F
u
m
du
d
u
du
d
m
m
m
m
m
m
m
m
m
m




























m=0
J0
K0 I0/50
N0

20. 1/24/2014 PHY 712 Spring 2014 -- Lecture 6 20
m=1
J1
N1
K1
I1/50