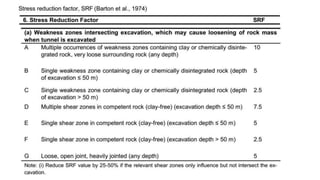
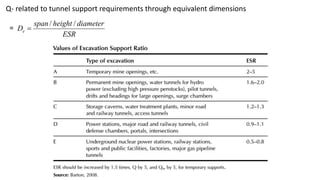
This document discusses different rock mass classification systems including Terzaghi, RMR, Q-System, and GSI. It provides details on calculating the Q value and parameters considered. Correlations are shown between RMR and Q values. Limitations of the Q-System are outlined. The Geological Strength Index (GSI) is introduced as a classification system for both hard and weak rocks based on rock structure and discontinuity conditions. A Hoek-Brown strength criterion for rock masses is also presented.