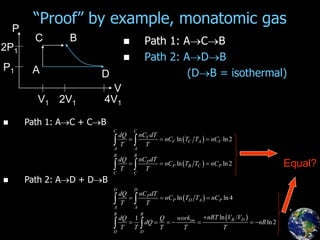
The document provides announcements and discussion about an upcoming exam review session, reading assignment, and thermodynamics concepts. It discusses finding entropy when temperature is constant or not, entropy change in free expansion, the difference between microstates and macrostates, and the relationship between probability and heat flow. The document also covers entropy as a state variable, entropy changes for different processes, and how the total entropy of the universe always increases.

1. Announcements 9/24/12
 Exam review session: Wed, 5-6:30 pm, room C295
 Reading assignment for Wednesday, see footnote in
syllabus:
a. Lecture 13 reading: 22.8, especially the marble
example but not the “Adiabatic Free Expansion: One
Last Time” example. Also: “What is entropy?” handout
posted to website, through Example 1.

2. From warmup
 Extra time on?
a. Finding entropy when T is not constant. Do we
need to do that? And I'm not sure how to find
entropy even when T is constant.
b. entropy change in a free expansion
c. Is change in entropy just change in Q?
d. micro & macrostates
 Other comments?
a. If this class kills me will 220 bring me back to life,
or will that be up to the religeon department?

3. Clicker question:
 Which of the following is a version of the Second Law of
Thermodynamics?
a. The entropy of any system decreases in all real processes
b. The entropy of any system increases in all real processes
c. The entropy of the Universe decreases in all real processes
d. The entropy of the Universe increases in all real processes

4. Second Law
 Clausius: Heat spontaneously flows from hot to
cold, not the other way around
 Why? Order.
 Which hand is more likely?
p.413a

5. Microstates vs Macrostates
 Hand on left
a. microstate = A spades, K spd, Q spd, J spd, 10 spd
b. macrostate = ?
c. How many microstates make up that macrostate?
 Hand on right
a. microstate = 2 spades, 3 diam, 7 heart, 8 clubs, Q diam
b. macrostate = ?
c. How many microstates make up that macrostate?
 The most common macrostates are those that…
p.413a

6. From warmup
 What's the difference between a macrostate
and a microstate?
a. A microstate is a single possible outcome,
where a macrostate is a group of
microstates fulfilling certain conditions

7. From warmup
 Which is most likely?
a. They all have exactly the same probability of
happening. It matters not where the dots are, or how
ordered they look, if the situation is exactly the same,
the probability is the same.
 How many of these “states” are there?
a. (only one student got it) There are "64 choose 8" =
4,426,165,368 total microstates like this. See here for
the formula if you are unfamiliar with it:
http://en.wikipedia.org/wiki/Combination

8. From warmup
 Same situation. Suppose a certain macrostate is composed
of all of the microstates where all of the occupied squares
touch at least one other occupied square (diagonally or
adjacent). Compare that to a second macrostate where
only 2 or fewer of the 8 occupied squares are touching
each other. Which of these macrostates is more likely?
a. The second one is more likely. The second macrostate
has more microstates in it.

9. Probability  Heat flow
 You separate a deck into two halves: one is
70% red, 30% black; the other is 30% red,
70% black. What will happen if you randomly
exchange cards between the two?

10. From warmup
 Consider all of the gas particles in the room where
you are sitting right now. Thinking about all the
positions, speeds, and directions of the particles in the
room, is this a likely macrostate? or an unlikely one?
Also, describe a macrostate (not microstate), for the
gas particles in this room, with the same energy that
is quite different from this one.
a. A likely one; No spontaneous transfers of energy
are occurring, and there are no hot or cold pockets
which aren't diffusing.
b. [Another macrostate would be where] The whole
room is cold, except for the burning hot air around
my untouched homework assignments, which catch
fire.

11. Thermodynamics
 For the air in this room, right now:
a. Microstate = ?
b. Macrostate = ?
Hold this thought until next time
The state the air is in will be “very close” to the one that has the
most number of microstates.
Next time: Entropy of a state  #Microstates in the state
The state the air is in will be “very close” to the one with the
highest entropy.
(Just called the “state”)

12. A New State Variable
 State variables we know: P, V, T, Eint
 Observation: doesn’t depend on path
 Something is a state variable!
 Assumption: path is well defined, T exists whole time
 “Internally reversible”
A
B
P
V
B
A
dQ
T


13. “Proof” by example, monatomic gas
 Path 1: ACB
 Path 2: ADB
(DB = isothermal)
 
 
 
 
ln ln2
ln ln2
ln ln4
ln
1
ln2
C C
V
V C A V
A A
B B
P
P B C P
C C
D D
P
P D A P
A A
B B
B D
on
D D
nC dT
dQ
nC T T nC
T T
nC dT
dQ
nC T T nC
T T
nC dT
dQ
nC T T nC
T T
nRT V V
work
dQ Q
dQ nR
T T T T T
  
  
  

      
 
 
 
 
A
B
P
V
C
D
V1 2V1 4V1
P1
2P1
 Path 1: AC + CB
 Path 2: AD + DB
Equal?

14. Entropy: S
 Assume S = 0 is defined somewhere.
(That’s actually the Third Law, not mentioned in your
textbook.)
 Integral only defined for internally reversible paths, but…
 S is a state variable!
…so it doesn’t matter what path you use to calculate it!
B
AB
A
dQ
S
T
  
Advertisement: On Wed I will explain
how/why this quantity is related to
microstates & macrostates

15. S for isothermal?
S for const. volume?
S for const. pressure?

16. S for “free expansion”
 What is V2? T2? P2?
 How to find S?
S for adiabatic?
 Adiabats = constant entropy contours
(“isentropic” changes)
 Wait… isn’t “free expansion” an adiabatic
process?
before after

17. S of Universe
 S of gas doesn’t depend on path (state variable):
 What about S of surroundings?
 What about Stotal = Sgas + Ssurroundings?
A
B
P
V
path1 path2
B
AB
A
dQ
S
T
S S
 
  

(See HW problem 12-4)

18. Thermodynamics Song
 http://www.uky.edu/~holler/CHE107/media/first_
second_law.mp3
(takes 4:13)