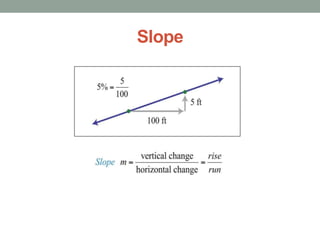
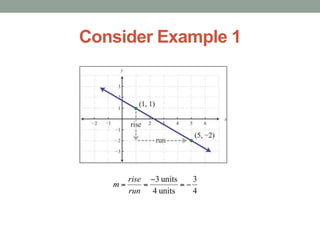
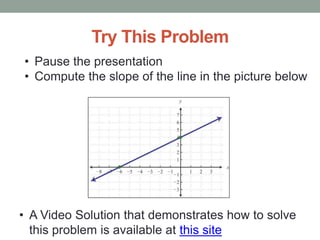
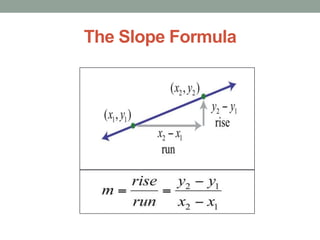
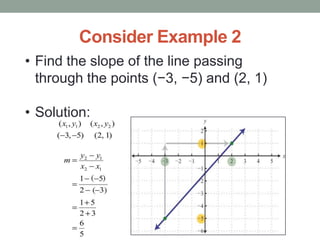
The document defines slope and explains how to calculate it using the rise over run formula. It provides two examples of computing slope, one using a graph and another using two coordinate points. The slope formula is defined and examples are worked through, with the second example calculating the slope of the line passing through points (-3, -5) and (2, 1).

1. Slope of Lines
• Learning Objective
• Define the slope formula of the line
• Compute values of slope using two examples

2. Slope

3. Rise and Run
• The rise can be positive or negative
• A positive rise corresponds to a vertical change up
• A negative rise corresponds to a vertical change down
• The run can be positive or negative
• A positive run corresponds to a horizontal change right
• A negative run corresponds to a horizontal change left

4. Consider Example 1

5. Try This Problem
• Pause the presentation
• Compute the slope of the line in the picture below
• A Video Solution that demonstrates how to solve
this problem is available at this site

6. The Slope Formula

7. Consider Example 2
• Find the slope of the line passing
through the points (−3, −5) and (2, 1)
• Solution: