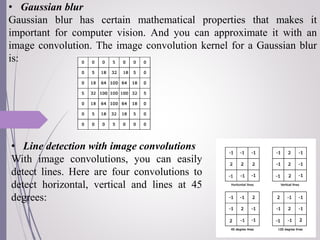
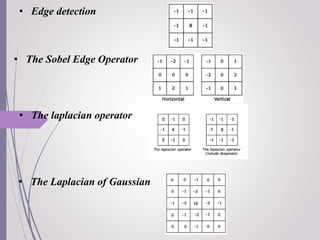
Image filtering is a technique for modifying or enhancing an image through the use of kernels or masks applied to each pixel and its neighbors. The process of applying filters to an image is called convolution, which can be done in either the spatial or frequency domain and relates the input, filtering kernel, and output signals. Convolution expresses how the input signal is changed by the filtering kernel and can be represented as the image convolved with the mask. Common filters include box blur for smoothing, Gaussian blur with important mathematical properties, and edge detection filters.

1. Lecture 5: Image Enhancement
Image Filtering
Computer Vision In MATLAB
By. Assist. Prof. Ielaf O.Abdul Majjed
2022-2023

2. Image filtering is a technique for modifying or enhancing an image
and its useful for many applications, including smoothing, sharpening,
removing noise, and edge detection. A filter is defined by a kernel or
mask , which is a small array applied to each pixel and its neighbors
within an image.
The process used to apply filters to an image is known as
convolution, and may be applied in either the spatial or frequency
domain.
Convolution is a mathematical operation on two signals that forms a
third signal. It expresses how the form of one is changed by the other
using the integral of the product of two functions after one is moved
over the other.
Convolution relates three signals of interest:
 input signal: an array of pixels (input image).
 filtering kernel: a small matrix of numbers that contains specific
coefficients
 output signal: a new modified filtered image

3. It can be explained as “image convolved with mask”.
g(x,y) = f(x,y) * h(x,y)
There are two ways to represent this because the convolution operator
(*) is commutative. The h(x,y) is the mask or filter.
Mask is also a signal. It can be represented by a two dimensional
matrix. The mask is usually of the order of 1x1, 3x3, 5x5, 7x7. A mask
should always be in odd number, because other wise you cannot find
the mid of the mask. Why do we need to find the mid of the mask.

6. • Simple box blur
Here's a first and simplest. This convolution kernel has an averaging
effect. So you end up with a slight blur. The image convolution kernel
is:
Note that the sum of all elements of this matrix is 1.0. This is
important. If the sum is not exactly one, the resultant image will be
brighter or darker.

7. • Gaussian blur
Gaussian blur has certain mathematical properties that makes it
important for computer vision. And you can approximate it with an
image convolution. The image convolution kernel for a Gaussian blur
is:
• Line detection with image convolutions
With image convolutions, you can easily
detect lines. Here are four convolutions to
detect horizontal, vertical and lines at 45
degrees:

8. • Edge detection
• The Sobel Edge Operator
• The laplacian operator
• The Laplacian of Gaussian

9. H.W:
• Low Pass Filter
• High Pass Filter