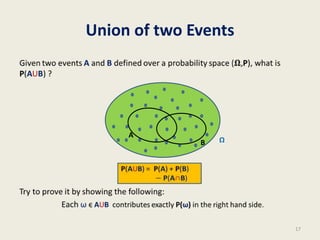
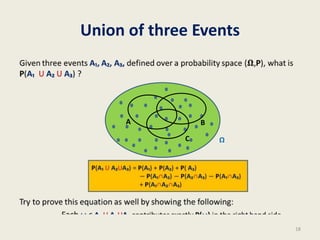
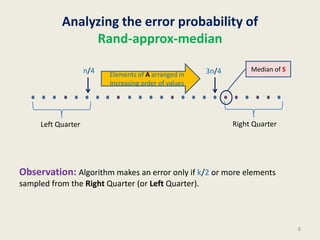
This document summarizes a lecture on randomized algorithms for approximating the median. It introduces a simple randomized algorithm called Rand-Approx-Median that takes an array as input and returns an element whose rank is approximately the median in O(log n log log n) time. The algorithm works by randomly sampling elements, sorting the samples, and returning the median of the sorted samples. The document analyzes the error probability of this algorithm using elementary probability theory and shows it has low error probability. It also emphasizes that designing and analyzing randomized algorithms requires insight into elementary probability concepts.

1. Randomized Algorithms
CS648
Lecture 2
• Randomized Algorithm for Approximate Median
• Elementary Probability theory
1

2. RANDOMIZED MONTE CARLO ALGORITHM
FOR
APPROXIMATE MEDIAN
2
This lecture was delivered at slow pace and its flavor was that of a
tutorial.
Reason: To show that designing and analyzing a randomized
algorithm demands right insight and just elementary probability.

3. A simple probability exercise
3

4. 4

5. Approximate median
Definition: Given an array A[] storing n numbers and ϵ > 0, compute an
element whose rank is in the range [(1- ϵ)n/2, (1+ ϵ)n/2].
Best Deterministic Algorithm:
• “Median of Medians” algorithm for finding exact median
• Running time: O(n)
• No faster algorithm possible for approximate median
5
Can you give a short proof ?

6. ½ - Approximate median
A Randomized Algorithm
Rand-Approx-Median(A)
1. Let k  c log n;
2. S  ∅;
3. For i=1 to k
4. x  an element selected randomly uniformly from A;
5. S  S U {x};
6. Sort S.
7. Report the median of S.
Running time: O(log n loglog n)
6

7. Analyzing the error probability of
Rand-approx-median
7
Elements of A arranged in
Increasing order of values
n/4 3n/4
Right QuarterLeft Quarter
When does the algorithm err ?
To answer this question, try to characterize what
will be a bad sample S ?

8. Analyzing the error probability of
Rand-approx-median
Observation: Algorithm makes an error only if k/2 or more elements
sampled from the Right Quarter (or Left Quarter).
8
n/4
Left Quarter Right Quarter
Elements of A arranged in
Increasing order of values
3n/4 Median of S

9. Analyzing the error probability of
Rand-approx-median
9
Elements of A arranged in
Increasing order of values
n/4 3n/4
Right QuarterLeft Quarter
Exactly the same as the coin
tossing exercise we did !
¼

10. Main result we discussed
10

11. ELEMENTARY PROBABILITY THEORY
(IT IS SO SIMPLE THAT YOU UNDERESTIMATE ITS ELEGANCE AND POWER)
11

12. Elementary probability theory
(Relevant for CS648)
• We shall mainly deal with discrete probability theory in this course.
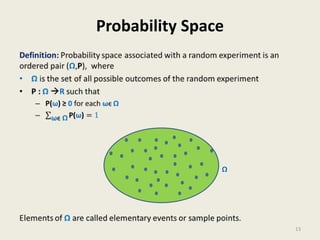
• We shall take the set theoretic approach to explain probability theory.
Consider any random experiment :
o Tossing a coin 5 times.
o Throwing a dice 2 times.
o Selecting a number randomly uniformly from [1..n].
How to capture the following facts in the theory of probability ?
1. Outcome will always be from a specified set.
2. Likelihood of each possible outcome is non-negative.
3. We may be interested in a collection of outcomes.
12

13. Probability Space
13
Ω

14. Event in a Probability Space
14
A
Ω

15. Exercises
A randomized algorithm can also be viewed as a random experiment.
1. What is the sample space associated with Randomized Quick sort ?
2. What is the sample space associated with Rand-approx-median
algorithm ?
15

16. An Important Advice
In the following slides, we shall state well known equations
(highlighted in yellow boxes) from probability theory.
• You should internalize them fully.
• We shall use them crucially in this course.
• Make sincere attempts to solve exercises that follow.
16

17. Union of two Events
17
A
B Ω

18. Union of three Events
18
A B
C Ω

19. Exercises
19

20. Conditional Probability
20

21. Exercises
• A man possesses five coins, two of which are double-headed, one is
double-tailed, and two are normal. He shuts his eyes, picks a coin at
random, and tosses it. What is the probability that the lower face of the
coin is a head ? He opens his eyes and sees that the coin is showing heads;
what it the probability that the lower face is a head ? He shuts his eyes
again, and tosses the coin again. What is the probability that the lower
face is a head ? He opens his eyes and sees that the coin is showing heads;
what is the probability that the lower face is a head ? He discards this coin,
picks another at random, and tosses it. What is the probability that it
shows heads ?
21

22. Partition of sample space and
an “important Equation”
22
Ω
B

23. Exercises
23

24. Independent Events
24
P(A ∩ B) = P(A) · P(B)

25. Exercises
25