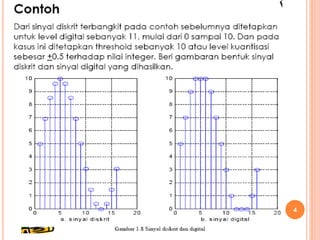
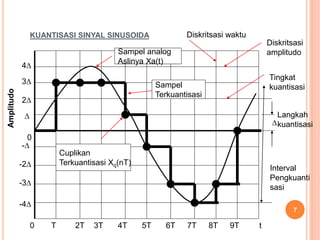
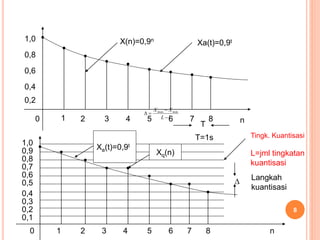
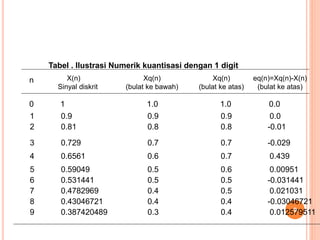
Teks tersebut membahas tentang proses kuantisasi sinyal kontinu menjadi sinyal digital. Kuantisasi melibatkan konversi nilai sinyal kontinu menjadi nilai diskrit dengan menggunakan ambang batas tertentu. Proses ini menghasilkan kesalahan kuantisasi yang diukur sebagai selisih antara nilai asli dan terkuantisasi. Teks tersebut juga menjelaskan konsep kuantisasi pada sinyal sinusoidal sebagai contoh kasus.

1. KUANTISASI
Qurrotul ‘Aini 1710501068
Maesaroh 1710501074
Teknik Elektro
Universitas Tidar

2. PENGETIAN KUANTISASI
Proses pengkonversian suatu sinyal amplitudo-
kontinu waktu diskrit menjadi sinyal digital dengan
menyatakan setiap nilai cuplikan sebagai suatu
angka digit, dinyatakan dengan :
    nXQnXq 
X(n) merupakan hasil pencuplikan,
Q[X(n)] merupakan proses kuantisasi
Xq( n) merupakan deret cuplikan terkuantisasi

3. KONSEP KUANTISASI (LANJUTAN)
Pada kasus sinyal digital, sinyal diskrit hasil proses
sampling diolah lebih lanjut. Sinyal hasil sampling
dibandingkan nilai threshold tertentu sesuai level –
level digital yang dikehendaki.
Apabila nilai sampel > threshold maka nilai digitalnya
mengikuti nilai integer diatasnya,
tetapi nilai sampel < threshold maka nilai digital
mengikuti nilai integer dibawahnya.
Proses ini dikenal sebagai kuantisasi dalam analog
to-digital conversion (ADC).
3

4. 4

5. 5

6. KESALAHAN KUANTISASI/
Kebisingan Kuantisasi /Galat Kuantisasi/
Error Kuantisasi
( eq(n) )
 Diperoleh dari kesalahan yang ditampilkan
oleh sinyal bernilai kontinu dengan
himpunan tingkat nilai diskrit berhingga.
 Sec Matematis, merupakan deret dari
selisih nilai terkuantisasi dengan nilai
cuplikan yang sebenarnya.
eq(n) = Xq (n) – X (n)
6

7. KUANTISASI SINYAL SINUSOIDA
7
0

2
3
4
-
-2
-3
-4
0 T 2T 3T 4T 5T 6T 7T 8T 9T t
Amplitudo
Cuplikan
Terkuantisasi Xq(nT)
Sampel
Terkuantisasi
Sampel analog
Aslinya Xa(t)
Tingkat
kuantisasi
Diskritsasi
amplitudo
Diskritsasi waktu

Langkah
kuantisasi
Interval
Pengkuanti
sasi

8. X(n)=0,9n
Xa(t)=0,9t
n1 2 3 4 5 6 7 80
1,0
0,8
0,6
0,4
0,2
T
T=1s
1 2 3 4 5 6 7 8
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0 n
Tingk. Kuantisasi
L=jml tingkatan
kuantisasi
 Langkah
kuantisasi
Xq(n)
Xa(t)=0,9t
1
minmax



L
XX
8

9. n X(n)
Sinyal diskrit
Xq(n)
(bulat ke bawah)
Xq(n)
(bulat ke atas)
eq(n)=Xq(n)-X(n)
(bulat ke atas)
0 1 1.0 1.0 0.0
1 0.9 0.9 0.9 0.0
2 0.81 0.8 0.8 -0.01
3 0.729 0.7 0.7 -0.029
4 0.6561 0.6 0.7 0.439
5 0.59049 0.5 0.6 0.00951
6 0.531441 0.5 0.5 -0.031441
7 0.4782969 0.4 0.5 0.021031
8 0.43046721 0.4 0.4 -0.03046721
9 0.387420489 0.3 0.4 0.012579511
Tabel . Ilustrasi Numerik kuantisasi dengan 1 digit
9

10. DAYA KESALAHAN KUADRAT RATA-RATA PQ
 dtteP qq 

 0
21
      tanatteq dim,2/
122
1 2
2
2
0






 
  dttPq


  tAtXa 0cos
10
Karena : , maka :
Pada gambar persamaan Sinyal Sinusoida analog :
menunjukkan waktu Xa(t) berada dalam tingkatan kuantisasi
Jika Pengkuantisasian b bit dan interval keseluruhan 2A,
maka langkah kuantisasi :  = 2A/2b. Jadi :
bq
A
P 2
2
2
3/

• Daya rata-rata sinyal Xa(t) :
  
pT
x
A
dttA
T
P
0
2
2
0
2
cos
1
