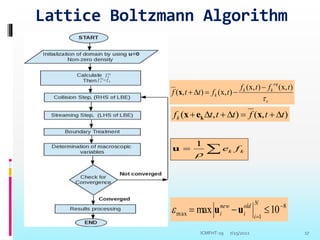
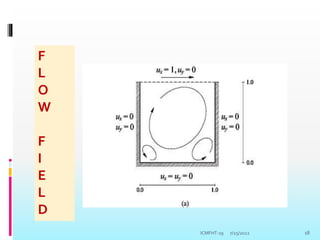
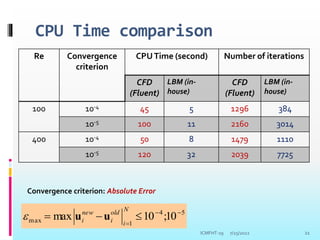
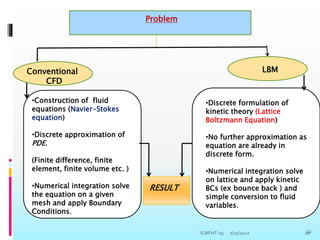
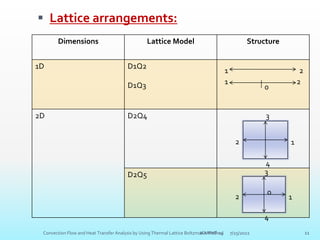
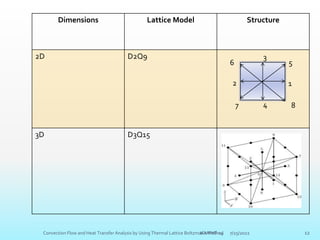
The document provides an introduction to the lattice Boltzmann method (LBM). It discusses that LBM is a kinetic method based on solving the Boltzmann equation for the particle distribution function. The lattice Boltzmann equation can be derived from the continuous Boltzmann equation. LBM involves discretizing the particle distribution function in velocity space and streaming and colliding particles on a lattice. It offers advantages over conventional CFD methods like easier treatment of complex boundaries and multi-phase flows.

1. INTRODUCTION TO LATTICE BOLTZMANN
METHOD
Department of Chemical Engineering
National Institute ofTechnology Rourkela, Rourkela-769008
7/25/2022 1
ICMFHT-19

2. 7/25/2022 3
Applications
Of LBM
ICMFHT-19

3. Lattice Boltzmann method
 LBM is kinetic method (Based on Boltzmann
equation).
 It is based on particle distribution function (DF)
f(x,e,t).
 LBM solves the kinetic Boltzmann equation for
f(x,t).
 Macroscopic quantities (u,ρ): Evaluation of
hydrodynamic moments of DF’s.
7/25/2022 4
ICMFHT-19

4.  The lattice Boltzmann equation is derived from Boltzmann
equation.
 The primary variable of interest is Particle Probability
Distribution function
 The Boltzmann equation is PDE delineating the evolution of
single particle distribution function ‘f’ in phase space.
 Boltzmann equation:
where, ‘f’ is particle distribution function,
‘e’ is particle velocity,
‘Ω’ is collision operator.
 ‘Ω’ is function of ‘f’; above equation is integro-differential
equation.
7/25/2022 5
)
,
,
( t
e
f x







k
k
f
e
t
f L
B
M
ICMFHT-19

5.  A suitable simplification of Ω is single
relaxation time approximation, called
Bhatnagar-Gross-Krook (BGK) model.
 The equation is linear PDE.
 It looks like advection equation with source
term.
 The LHS side of equation represents
streaming, while RHS represents collision
term.
7/25/2022 6
 
eq
k
k f
f 




1
 
eq
k
k
k
k
f
f
f
t
f









1
x
ICMFHT-19

6.  The discretization in space and time of
Boltzmann equation,
 Local equilibrium distribution function
along with relaxation time (τ) limits the
applicability of LBM.
 Relation of relaxation time with kinematic
viscosity is given as
7/25/2022 7
 
)
,
(
)
,
(
)
,
(
)
,
( t
f
t
f
t
t
f
t
t
t
e
f k
eq
k
k
k
k x
x
x
x 








eq
k
f
 
5
.
0
3
1

 

ICMFHT-19

7. The Lattice Boltzmann Method:
From the Boltzmann equation (continued)
 The lattice Boltzmann equation can be rigorously derived from
the continuous Boltzmann equation (He and Luo 1997) and is
given by:
 where τ is the dimensionless relaxation time (τ = λ/δt), α indicates
the discrete velocity direction, and the equilibrium distribution
function, f eq, is given by:

 where c is the speed at which a distribution function moves, i.e.
δx/δt.


 



)
,
(
)
,
(
)
,
(
)
,
(
t
x
f
t
x
f
t
x
f
t
e
x
f
eq
t
t
















 2
2
4
2
2
2
3
2
u)
(e
9
u
e
1
c
u
c
c
w
f eq 


 
7/25/2022
ICMFHT-19 8

8. Equilibrium distribution function
 Different physical problems can be solved by LBM,
by using proper equilibrium distribution function.
 For system of particles moving in a medium with
velocity u, Maxwell’s distribution function,
 The Taylor-Series expansion of above equation
(similar to ),
7/25/2022 9
2
2
)
)(
(
2
3
)
(
2
3
3
/
2
3
/
2
u
u
u
e
e
e
u
e 







 e
e
f eq




x
e











....
)
(
2
3
)
(
3
1
3
/
2
)
(
2
3
u.u
e.u
e.e
e
f eq


ICMFHT-19

9.  In general form,
 χ is scalar parameter
7/25/2022 10
 
)
(
)
(
)
( 2
u.u
.u
e
.u
e k
k D
C
B
A
w
f k
eq
k 


 



n
k
eq
k
f
0

ICMFHT-19

10.  Lattice arrangements:
7/25/2022
Convection Flow and Heat Transfer Analysis by Using Thermal Lattice Boltzmann Method 11
Dimensions Lattice Model Structure
1D D1Q2
D1Q3
2D D2Q4
D2Q5
2
3
1
4
2
3
1
4
0
1 2
1 2
0
7/25/2022 11
ICMFHT-19

11. 7/25/2022
Convection Flow and Heat Transfer Analysis by Using Thermal Lattice Boltzmann Method 12
Dimensions Lattice Model Structure
2D D2Q9
3D D3Q15
2
3
1
4
5
6
7 8
7/25/2022 12
ICMFHT-19

12. 7/25/2022 13
EVOLUTION OF PARTICLE DISTRIBUTION
FUNCTION IN LBE
STREAMING
)
,
(
)
,
( t
x
f
t
t
t
c
x
f k
k
k






COLLISION
)]
,
(
)
,
(
[
1
)
,
(
)
,
( t
x
f
t
x
f
t
x
f
t
x
f k
eq
k
k
k 




13
ICMFHT-19

13. 7/25/2022 14
 
)
,
(
)
,
(
1
)
,
(
)
,
( t
f
t
f
t
f
t
t
t
f
eq
k
k
v
k
k x
x
x
e
x k 








Flow Field
,
)
.
(
2
3
)
(
2
9
)
(
3
1 2
4
2
2














c
c
e
c
e
w
f k
k
k
eq
k
u
u
u
u

1
3 0.5
v
 

  
8 8
0 0
1
;
k k
k k k
k k
f f e


 
 
 
 
u
36
1
,
9
1
,
9
4
,
D2Q9
for
function,
weight
is
w
8
,
7
,
6
,
5
4
,
3
,
2
,
1
0
k



w
w
w
1
x t
   
ICMFHT-19

14. Boundary Conditions
 Bounce Back: The method is quite simple and
mainly implies that an incoming particle towards
the solid boundary bounces back
into flow domain.
7/25/2022 15
ICMFHT-19

15. Lattice Boltzmann Algorithm
7/25/2022 17
v
eq
k
k
k
t
f
t
f
t
f
t
t
f

)
,
x
(
)
,
x
(
)
,
x
(
)
,
(





x
)
,
(
)
,
( t
t
f
t
t
t
fk 





 x
e
x k

 k
k f
e

1
u
8
1
max 10
max 




N
i
old
i
new
i u
u

ICMFHT-19

16. 7/25/2022 18
F
L
O
W
F
I
E
L
D
ICMFHT-19

17. CPU Time comparison
7/25/2022 21
Re Convergence
criterion
CPUTime (second) Number of iterations
CFD
(Fluent)
LBM (in-
house)
CFD
(Fluent)
LBM (in-
house)
100 10-4 45 5 1296 384
10-5 100 11 2160 3014
400 10-4 50 8 1479 1110
10-5 120 32 2039 7725
Convergence criterion: Absolute Error
5
4
1
max 10
;
10
max 





N
i
old
i
new
i u
u

ICMFHT-19

18. 7/25/2022 22
Problem
Conventional
CFD
LBM
•Construction of fluid
equations (Navier-Stokes
equation)
•Discrete approximation of
PDE.
(Finite difference, finite
element, finite volume etc. )
•Numerical integration solve
the equation on a given
mesh and apply Boundary
Conditions.
•Discrete formulation of
kinetic theory (Lattice
Boltzmann Equation)
•No further approximation as
equation are already in
discrete form.
•Numerical integration solve
on lattice and apply kinetic
BCs (ex bounce back ) and
simple conversion to fluid
variables.
RESULT
22
ICMFHT-19

19. Advantages
 It is easy to apply for complex domains due to easy nature of
boundary conditions.
 Easy to treat multi-phase and multi-component flows without
a need to trace the interfaces between different phases.
 It can be naturally adapted to parallel processes computing.
 Moreover, there is no need to solve Laplace equation at each
time step to satisfy continuity equation of incompressible,
unsteady flows, as it is in solving Navier–Stokes (NS) equation.
7/25/2022 23
ICMFHT-19

20.  It can handle a problem in micro- and macro-
scales with reliable accuracy.
 Automated data pre-processing and mesh
generation in a time that accounts for a small
fraction of the total simulation.
7/25/2022 24
ICMFHT-19

21. Disadvantages
 It needs more computer memory compared
with NS solver.
 At present, high-Mach number flows in
aerodynamics are still difficult for LBM.

7/25/2022 25
ICMFHT-19

22. Suggested Reading
7/25/2022 26
•Mohamad A.A., Fundamentals and Engineering Applications with
Computer Codes, Springer, Springer-Verlag London Limited
2011.
•Succi, Sauro (2001). The Lattice Boltzmann Equation for Fluid
Dynamics and Beyond. Oxford University Press. ISBN 0-19-850398-9.
•Wolf-Gladrow, Dieter (2000). Lattice-Gas Cellular Automata and
Lattice Boltzmann Models. Springer Verlag. ISBN 978-3-540-66973-9.
•Sukop, Michael C.; Daniel T. Thorne, Jr. (2007). Lattice Boltzmann
Modeling: An Introduction for Geoscientists and Engineers. Springer.
ISBN 978-3-540-27981-5.
•Jian Guo Zhou (2004). Lattice Boltzmann Methods for Shallow Water
Flows. Springer. ISBN 3-540-40746-4.
•He,X., Chen, S., Doolen, G. (1998). A Novel Thermal Model for the
Lattice Boltzmann Method in Incompressible Limit. Academic Press.
ICMFHT-19

23. 7/25/2022 27
ICMFHT-19