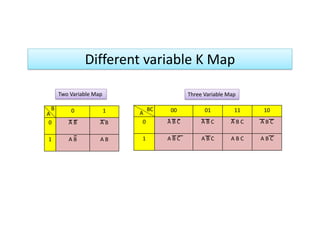
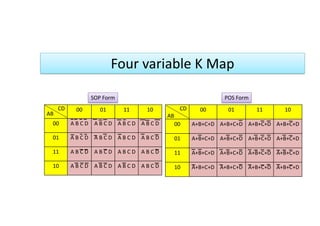
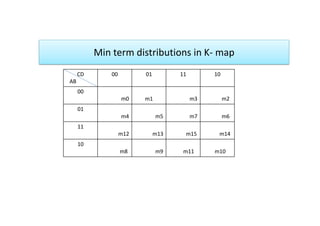
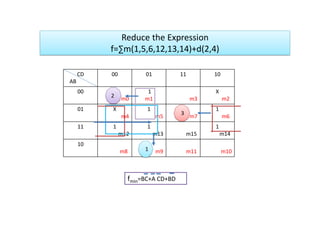
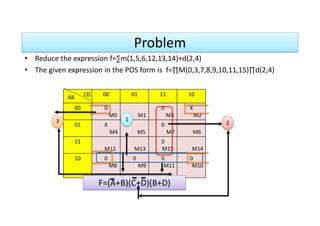
The document presents techniques for minimizing sum of products (SOP) and product of sums (POS) expressions using Karnaugh maps. It includes examples of two, three, and four-variable maps and demonstrates the process of reducing expressions through various methodologies. Key expressions and their simplified forms are provided, illustrating the application of Karnaugh maps for logical expression minimization.

1. Minimization of SOP and POS
Expressions using Karnaugh
map
Prepared by- Dr. Sutapa Mukherjee

2. Different variable K Map
0 1
0 A B A B
1 A B A B
A
B 00 01 11 10
0 A B C A B C A B C A B C
1 A B C A B C A B C A B C
A
BC
Two Variable Map Three Variable Map

3. Four variable K Map
00 01 11 10
00 A B C D A B C D A B C D A B C D
01 A B C D A B C D A B C D A B C D
11 A B C D A B C D A B C D A B C D
10 A B C D A B C D A B C D A B C D
AB
CD 00 01 11 10
00 A+B+C+D A+B+C+D A+B+C+D A+B+C+D
01 A+B+C+D A+B+C+D A+B+C+D A+B+C+D
11 A+B+C+D A+B+C+D A+B+C+D A+B+C+D
10 A+B+C+D A+B+C+D A+B+C+D A+B+C+D
CD
AB
POS Form
SOP Form

4. Min term distributions in K- map
CD 00 01 11 10
00
m0 m1 m3 m2
01
m4 m5 m7 m6
11
m12 m13 m15 m14
10
m8 m9 m11 m10
AB

5. Reduce the Expression
f=∑m(1,5,6,12,13,14)+d(2,4)
CD 00 01 11 10
00
m0
1
m1 m3
X
m2
01 X
m4
1
m5 m7
1
m6
11 1
m12
1
m13 m15
1
m14
10
m8 m9 m11 m10
AB
2
3
1
fmin=BC+A CD+BD

6. Problem
• Reduce the expression f=∑m(1,5,6,12,13,14)+d(2,4)
• The given expression in the POS form is f=∏M(0,3,7,8,9,10,11,15)∏d(2,4)
00 01 11 10
00 0
M0 M1
0
M3
X
M2
01 X
M4 M5
0
M7 M6
11
M12 M13
0
M15 M14
10 0
M8
0
M9
0
M11
0
M10
AB CD
F=(A+B)(C+D)(B+D)
2
3 1